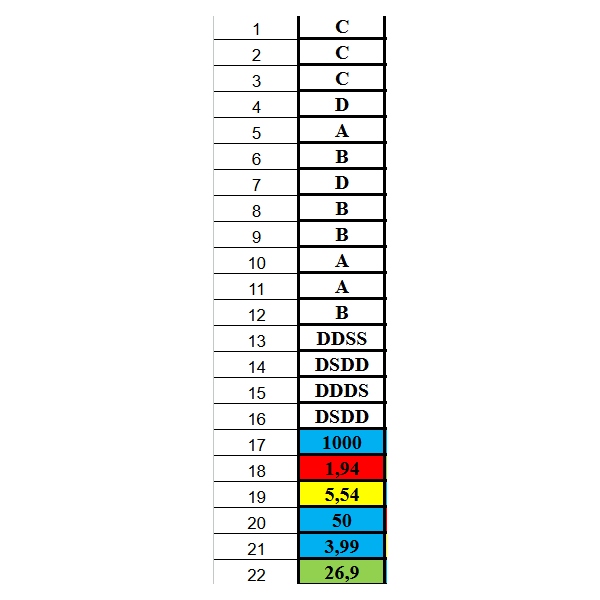
Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn
Thí sinh trả lời từ Câu 1 đến Câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1:
Đồ thị của hàm số $y = x^3 – 3x + 1$ có dạng như đường cong nào dưới đây?

A.
B.
C.
D.
Câu 2:
Cho hình hộp $ABCD.A’B’C’D’$. Kí hiệu $\vec{a} = \overrightarrow{AA’}$, $\vec{b} = \overrightarrow{AB}$, $\vec{c} = \overrightarrow{AD}$ và $O$ là tâm của mặt bên $CC’B’B$ (tham khảo hình vẽ sau).

Hãy biểu diễn vector $\overrightarrow{AO}$ theo các vector $\vec{a}, \vec{b}, \vec{c}$.
A. $\overrightarrow{AO} = \vec{a} + \vec{b} + \vec{c}$
B. $\overrightarrow{AO} = -\vec{a} + \frac{1}{2}\vec{b} + \frac{1}{2}\vec{c}$
C. $\overrightarrow{AO} = \frac{1}{2}\vec{a} + \frac{1}{2}\vec{b} + \frac{1}{2}\vec{c}$
D. $\overrightarrow{AO} = \frac{1}{2}\vec{a} + \frac{1}{2}\vec{b} + \frac{1}{2}\vec{c}$
Câu 3:
Tiệm cận ngang của đồ thị hàm số $y = \frac{x-2}{x+1}$ là đường thẳng có phương trình
A. $x = 2$
B. $x = -1$
C. $y = 1$
D. $y = -2$
Câu 4:
Cho hàm số $f(x)$ có bảng xét dấu của đạo hàm như sau
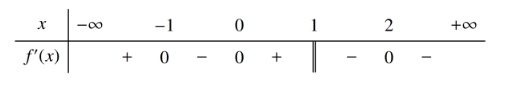
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. $(1; 2)$
B. $(-1; 1)$
C. $(1; +\infty)$
D. $(-\infty; -1)$
Câu 5:
Đồ thị hàm số $y = \frac{1}{2}x^3 – 3x^2 + 5x – 3$ có tâm đối xứng là điểm
A. $M(2; -1)$
B. $P(-2; -29)$
C. $N(2; 1)$
D. $Q\left(1; -\frac{1}{2}\right)$
Câu 6:
Tiệm cận xiên của đồ thị hàm số $y = 2x – 1 – \frac{3}{x+1}$ là đường thẳng có phương trình
A. $y = 2x + 1$
B. $y = 2x – 1$
C. $y = x + 1$
D. $x = -1$
Câu 7:
Đồ thị của hàm số nào dưới đây có dạng như đường cong ở hình sau?
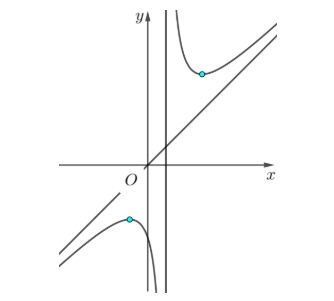
A. $y = -x – \frac{4}{x-1}$
B. $y = x – \frac{4}{x-1}$
C. $y = -x + \frac{4}{x-1}$
D. $y = x + \frac{4}{x-1}$
Câu 8:
Giá trị lớn nhất của hàm số $y = x^4 – 4x^2 + 9$ trên đoạn $[-2; 3]$ bằng
A. 9
B. 54
C. 2
D. 201
Câu 9:
Trong không gian $Oxyz$, cho điểm $M$ thỏa mãn $\overrightarrow{OM} = 2\vec{i} – \vec{j} + 3\vec{k}$. Tọa độ của điểm đã cho là
A. $(2; 1; 3)$
B. $(2; -1; 3)$
C. $(3; -1; 2)$
D. $(-1; 2; 3)$
Câu 10:
Cho hàm số $y = f(x)$ xác định và liên tục trên $\mathbb{R}$ có đồ thị như hình vẽ sau.

Tìm giá trị nhỏ nhất $m$ và giá trị lớn nhất $M$ của hàm số đã cho trên đoạn $[-2; 2]$.
A. $m = -5; M = -1$
B. $m = -5; M = 0$
C. $m = -2; M = 2$
D. $m = -1; M = 0$
Câu 11:
Cho hình lập phương $ABCD.A’B’C’D’$. Hãy tính góc giữa hai vectơ vectơ $\overrightarrow{AC}$ và $\overrightarrow{DC’}$.

A. $60°$
B. $45°$
C. $90°$
D. $120°$
Câu 12:
Cho hàm số $y = f(x)$ có bảng biến thiên như sau

Cực đại của hàm số đã cho là
A. $-2$
B. $4$
C. $3$
D. $-3$
PHẦN II. Câu trắc nghiệm đúng sai
Thí sinh trả lời từ Câu 13 đến Câu 16. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13:
Cho hàm số $y = \frac{x^2}{x-1}$ có đồ thị là $(C)$.
A. Nếu $M\left(m; \frac{m^2}{m-1}\right)$ là điểm thuộc $(C)$ thì $M’\left(2-m; \frac{-m^2+4m-4}{m-1}\right)$ cũng là điểm thuộc $(C)$.
B. Giao điểm của tiệm cận đứng và tiệm cận xiên của $(C)$ là tâm đối xứng của $(C)$.
C. Đường thẳng đi qua hai điểm cực trị của $(C)$ là một trục đối xứng của $(C)$.
D. Nếu $y_1$ và $y_2$ lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số đã cho thì $y_1$ lớn hơn $y_2$.
Câu 14:
Cho hàm số $y = f(x)$, với $f(x) = ax^3 + bx^2 + cx + d$. Biết đồ thị của hàm số đã cho có hai điểm cực trị là $A(-1; 1)$ và $B(1; -3)$ (tham khảo hình vẽ sau)

A. Nếu $x_1, x_2$ thuộc đoạn $[-1; 1]$ mà $x_1 < x_2$ thì $f(x_1) > f(x_2)$.
B. Đa thức $3ax^2 + 2bx + c$ có duy nhất một nghiệm.
C. Hàm số đã cho đồng biến trên khoảng $(1; +\infty)$.
D. Tập xác định của hàm số đã cho là $\mathbb{R}$.
Câu 15:
Cho hàm số $f(x) = \frac{x-1}{\sqrt{x^2+1}}$.
A. Nếu $K$ là một khoảng bất kì chứa điểm $x = -1$ thì $f(x) > f(-1)$ với mọi $x \in K \setminus {-1}$.
B. Tập xác định của hàm số là $\mathbb{R}$.
C. Đạo hàm của hàm số đã cho là $f'(x) = \frac{x+1}{(x^2+1)\sqrt{x^2+1}}$
D. Giá trị nhỏ nhất của hàm số đã cho trên $\mathbb{R}$ bằng $1,414213562$.
Câu 16:
Trong không gian $Oxyz$, cho bốn điểm $A(2; 1; 1)$, $B(1; 3; 1)$, $C(2; 2; 2)$, $D(3; 2; 0)$. Gọi $M$ là trung điểm của đoạn thẳng $BC$.
A. Giá trị gần đúng của $\widehat{BMA}$, tính theo đơn vị độ và làm tròn đến hàng phần mười, là $51,5°$.
B. Độ dài của các vectơ $\overrightarrow{MD}$ và $\overrightarrow{MA}$ lần lượt là $\frac{\sqrt{11}}{2}$ và $\frac{\sqrt{19}}{2}$.
C. Tọa độ của điểm $M$ là $\left(\frac{3}{2}; \frac{5}{2}; \frac{3}{2}\right)$.
D. Tọa độ của các vectơ $\overrightarrow{MD}$ và $\overrightarrow{MA}$ lần lượt là $\left(\frac{3}{2}; -\frac{1}{2}; -\frac{3}{2}\right)$ và $\left(\frac{1}{2}; -\frac{3}{2}; -\frac{1}{2}\right)$.
PHẦN III. Câu trắc nghiệm trả lời ngắn
Thí sinh trả lời từ Câu 17 đến Câu 22.
Câu 17:
Tính gần đúng, làm tròn đến hàng đơn vị, giá trị cực tiểu của hàm số
$V = 999,87 – 0,06426T + 0,00850437T^2 – 0,00007697T^3$.
Câu 18:
Tính gần đúng, làm tròn đến hàng phần trăm, giá trị nhỏ nhất của hàm số
$f(x) = \frac{1}{3-x} + \frac{2}{x}$ trên khoảng $(0; 3)$.
Câu 19:
Người ta cần thiết kế một cái lon có dạng hình trụ có thể tích là 1 lít, bằng sắt là tráng thiếc có độ dày cho trước. Xét các lon có thể tích 1 lít như vậy, kí hiệu $(L_n)$ là cái lon có diện tích bề mặt (diện tích toàn phần) nhỏ nhất. Hỏi diện tích bề mặt của $(L_n)$ là bao nhiêu decímet vuông (làm tròn đến hàng phần trăm)?

Câu 20:
Đối với sản phẩm của một nhà độc quyền, hàm chi phí trung bình là $\bar{c} = 0,004q^2 + 20 + \frac{5000}{q}$ và hàm cầu là $p = 450 – 4q$; trong đó $q$ là số lượng đơn vị sản phẩm, cả $p$ và $\bar{c}$ đều được tính bằng đô la trên mỗi đơn vị sản phẩm. Hãy tìm mức sản lượng mà tại đó lợi nhuận được tối đa hóa.
Giải thích các thuật ngữ:
- Hàm cầu: Mô tả mối quan hệ giữa giá cả sản phẩm và lượng hàng hóa mà người tiêu dùng sẵn sàng mua.
- Hàm chi phí trung bình: Cho biết chi phí trung bình để sản xuất một đơn vị sản phẩm.
- Lợi nhuận: Là hiệu số giữa doanh thu tổng và chi phí tổng.
- Tối đa hóa lợi nhuận: Tìm mức sản lượng và giá cả mà tại đó lợi nhuận đạt giá trị lớn nhất.
Câu 21:
Thể tích $V$ của 1 kg nước (tính bằng $cm^3$) ở nhiệt độ $T$ (đơn vị: $°C$) khi $T$ thay đổi từ $0°C$ đến $30°C$ được cho xấp xỉ bởi công thức:
$V = 999,87 – 0,06426T + 0,00850437T^2 – 0,00007697T^3$.
Kí hiệu $T_0$ là giá trị nhỏ nhất của $T$ thuộc khoảng $(0; 30)$ mà kể từ nhiệt độ $T_0$ trở lên thì thể tích $V$ tăng.
Tính gần đúng, làm tròn đến hàng phần trăm, giá trị của $T_0$.
Câu 22:
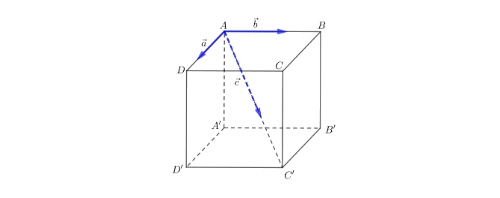
Một chất điểm ở vị trí đỉnh $A$ của hình lập phương $ABCD.A’B’C’D’$ với AB=2, AD=1, AA’=2. Chất điểm chịu tác động bởi ba lực $\vec{a}$, $\vec{b}$ và $\vec{c}$ lần lượt cùng hướng với $\overrightarrow{AD}$, $\overrightarrow{AB}$ và $\overrightarrow{AC’}$ (tham khảo hình vẽ). Cường độ của các lực $\vec{a}$, $\vec{b}$ và $\vec{c}$ trong trọng tâm là 10N, 10N và 15N. Hỏi, cường độ hợp lực tác động lên chất điểm là bao nhiêu newton (làm tròn đến hàng phần chục)?

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh