Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12, mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Cho hàm số $y = \frac{-2x + 1}{x – 1}$. Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên tập $(-\infty; 1) \cup (1; +\infty)$.
B. Hàm số nghịch biến trên các khoảng $(-\infty; 1)$ và $(1; +\infty)$.
C. Hàm số nghịch biến trên tập $\mathbb{R} \setminus {-1}$.
D. Hàm số nghịch biến trên các khoảng $(-\infty; -1)$ và $(-1; +\infty)$.
Câu 2. Dũng là học sinh rất giỏi chơi rubik, bạn có thể giải nhiều loại khối rubik khác nhau. Trong một lần tập luyện giải khối rubik $3 \times 3$, bạn Dũng đã tự thống kê lại thời gian giải rubik trong 25 lần giải liên tiếp ở bảng sau:

Độ lệch chuẩn của mẫu số liệu ghép nhóm có giá trị gần nhất với giá trị nào dưới đây?
A. 5,98.
B. 6.
C. 2,44.
D. 2,5.
Câu 3. Tìm giá trị nhỏ nhất $m$ của hàm số $y = x^4 – x^2 + 13$ trên đoạn $[-2; 3]$.
A. $m = \frac{51}{4}$.
B. $m = \frac{49}{4}$.
C. $m = 13$.
D. $m = \frac{51}{2}$
Câu 4. Cho hàm số $y = f(x)$ có bảng biến thiên như sau
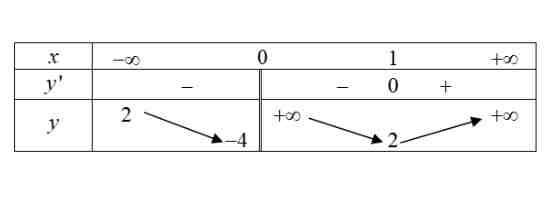
Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số là.
A. 4.
B. 1.
C. 2.
D. 3.
Câu 5. Cho hàm số $y = f(x)$ có bảng biến như sau:
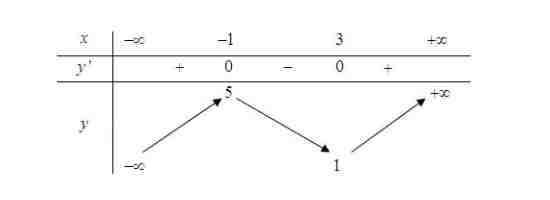
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. $(1; 5)$.
B. $(3; +\infty)$.
C. $(-1; 3)$
D. $(0; 4)$.
Câu 6: Trong không gian $Oxyz$, cho tam giác $ABC$ biết $A(5; 0; -2)$, $B(3; 1; 4)$, $C(1; 2; 1)$. Trọng tâm $G$ của tam giác $ABC$ có tọa độ là:
A. $(9; 3; 3)$
B. $(-9; -3; -3)$
C. $(-3; -1; -1)$
D. $(3; 1; 1)$
Câu 7: Trong không gian $Oxyz$, cho vector $\vec{u} = 2\vec{i} + 3\vec{j} – 4\vec{k}$. Tọa độ vector $\vec{u}$ là
A. $(2; 3; -4)$
B. $(-2; -3; 4)$
C. $(2; -3; 4)$
D. $(2; 3; 4)$
Câu 8: Trong không gian với hệ trục tọa độ $Oxyz$, cho ba điểm $A(1; 2; -1)$, $B(2; -1; 3)$, $C(-2; 3; 3)$. Điểm $M(a; b; c)$ thỏa mãn $\overrightarrow{AB} = \overrightarrow{MC}$. Khi đó $P = a^2 + b^2 – c^2$ có giá trị bằng
A. 45.
B. 42.
C. 44.
D. 43.
Câu 9: Trong các hàm số sau, hàm số nào đồng biến trên $\mathbb{R}$?
A. $y = \frac{2x – 1}{x – 3}$.
B. $y = x^3 + 2x – 2022$.
C. $y = x^3 + 2x – 1$.
D. $y = x^3 – 2x^2$.
Câu 10: Cho hàm số bậc ba $y = f(x)$ có đồ thị là đường cong trong hình bên dưới:
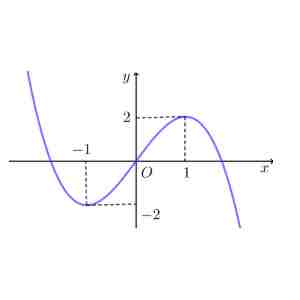
Số nghiệm thực của phương trình là $f(x) = 3$
A. 1.
B. 0.
C. 2.
D. 3.
Câu 11: Cho tứ diện $ABCD$. Gọi $P, Q$ là trung điểm của $AB$ và $CD$. Chọn khẳng định đúng?
A. $\overrightarrow{PQ} = \frac{1}{2}(\overrightarrow{BC} + \overrightarrow{AD})$.
B. $\overrightarrow{PQ} = \frac{1}{2}(\overrightarrow{BC} + \overrightarrow{AD})$.
C. $\overrightarrow{PQ} = \frac{1}{2}(\overrightarrow{BC} – \overrightarrow{AD})$.
D. $\overrightarrow{PQ} = \overrightarrow{BC} + \overrightarrow{AD}$.
Câu 12: Trong không gian với hệ tọa độ $Oxyz$, cho các vector $\vec{a} = (2; m – 1; 3)$, $\vec{b} = (1; 3; -2n)$. Tìm $m, n$ để các vector $\vec{a}, \vec{b}$ cùng hướng.
A. $m = 7; n = -\frac{3}{4}$.
B. $m = 4; n = -3$.
C. $m = 1; n = 0$.
D. $m = 7; n = -\frac{4}{3}$.
PHẦN II. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đổi cháy các tên lửa hãm ở độ cao 250 km so với bề mặt của Mặt Trăng. Trong khoảng 50 giây đầu tiên kể từ khi đổi cháy các tên lửa hãm, độ cao h của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm $h(t) = -0,01t^3 + 1,1t^2 – 30t + 250$, vận tốc của tàu được tính như sau: $v(t) = h'(t)$ trong đó $t$ là thời gian tính bằng giây và $h$ là độ cao tính bằng kilômét.
a) Xét thời điểm $0 \leq t \leq 50$ thì tại thời điểm $t \approx 18$ giây thì con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng và khoảng cách nhỏ nhất này bằng 8,08 km.
b) Đồ thị của hàm số $y = h(t)$ với $0 \leq t \leq 70$ (đơn vị trên trục hoành là 10 giây, đơn vị trên trục tung là 50 km) như sau:
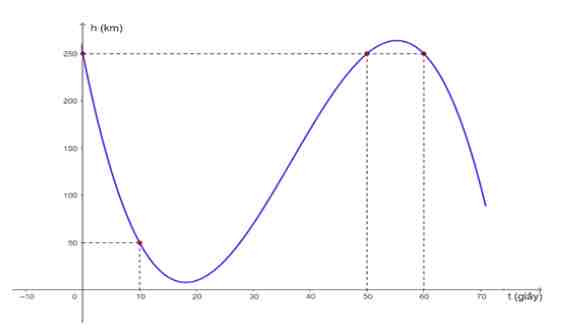
c) Gọi $v(t)$ là vận tốc tức thời của con tàu ở thời điểm $t$ (giây) kể từ khi đổi cháy các tên lửa hãm với $0 \leq t \leq 50$. Vận tốc tức thời của con tàu tại thời điểm $t = 25$ (giây) là 5,25 km/s.
d) Tại thời điểm $t = 25$ (giây), vận tốc tức thời của con tàu vẫn giảm.
Câu 2. Một bác tài xế thống kê lại độ dài quãng đường (đơn vị: km) bác đã lái xe mỗi ngày trong một tháng ở bảng sau:

a) Khoảng biến thiên của mẫu số liệu ghép nhóm là 250 (km).
b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm gần bằng $79,17$.
c) Số trung bình của mẫu số liệu ghép nhóm là $145$.
d) Độ lệch chuẩn của mẫu số liệu ghép nhóm gần bằng
Câu 3. Trong không gian với hệ trục tọa độ $Oxyz$, cho hình hộp chữ nhật $ABCD.A’B’C’D’$ có điểm $A$ trùng với gốc tọa độ $O$, điểm $B$ nằm trên tia $Ox$, điểm $D$ nằm trên tia $Oy$, điểm $A’$ nằm trên tia $Oz$. Biết $AB = 2$, $AD = 4$, $AA’ = 3$. Gọi tọa độ của $C’$ là $(a; b; c)$.
a) Tọa độ của điểm $B$ là $(2; 0; 0)$.
b) Tọa độ của $\overrightarrow{AD}$ là $(4; 0; 0)$.
c) Tọa độ của điểm $C$ là $(2; 4; 0)$.
d) $a + b – c = -3$.
Câu 4. Hình minh họa sơ đồ một ngôi nhà trong hệ trục tọa độ $Oxyz$, trong đó nền nhà, bốn bức tường và hai mái nhà đều là hình chữ nhật.

a) Tọa độ của các điểm $A(5; 0; 0)$.
b) Tọa độ của các điểm $H(0; 5; 3)$.
c) Góc nhị diện có cạnh là đường thẳng $FG$, hai mặt lần lượt là $(FGOP)$ và $(FGHE)$ gọi là góc dốc của mái nhà. Số đo của góc dốc của mái nhà bằng $26,6°$ (làm tròn kết quả đến hàng phần mười của độ).
d) Chiều cao của ngôi nhà tính đến đỉnh mái nhà là 4.
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu ……
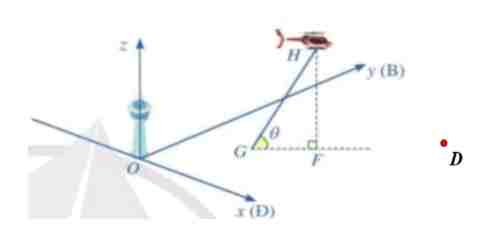
Câu 1. Một chiếc trực thăng $H$ cất cánh từ một sân bay. Xét hệ trục tọa độ $Oxyz$ có gốc tọa độ $O$ là chân tháp điều khiển sân bay; trục $Ox$ là hướng đông, trục $Oy$ là hướng bắc và trục $Oz$ là trục thẳng đứng, đơn vị trên mỗi trục là kilômét. Trực thăng cất cánh yư điểm $G$ trên mặt đất (mặt phẳng $Oxy$). Vị trí của trực thăng tại thời điểm $t$ phút sau khi cất cánh $(t \geq 0)$ có tọa độ là $M\left(\frac{8}{3} + t; \frac{1}{2} + 2t; 2\frac{6}{8}\right)$. Một hòn đảo ở vị trí $D(150; 115; 0)$ (hình vẽ minh họa). Máy bay $H$ bay đến vị trí $M_0(x_0; y_0; z_0)$ thì khoảng cách từ máy bay đến $D$ là nhỏ nhất. Tính $T = 20(x_0 + y_0 + z_0)$.
Câu 2. Trong không gian chọn hệ trục tọa độ cho trước, đơn vị đo lấy kilômét, ra đa phát hiện một máy bay chiến đấu của Mỹ di chuyển với vận tốc và hướng không đổi từ điểm $M(1000; 600; 14)$ đến điểm $N(a; b; c)$ trong 30 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của máy bay sau 10 phút tiếp theo bằng $Q(1400; 800; 16)$. Tính $T = a + b + 2c$

Câu 3. Một ống khói của nhà máy điện hạt nhân có mặt cắt là một hypebol (H) có phương trình chính tắc là: $\frac{x^2}{27^2} – \frac{y^2}{40^2} = 1$ (Hình vẽ).
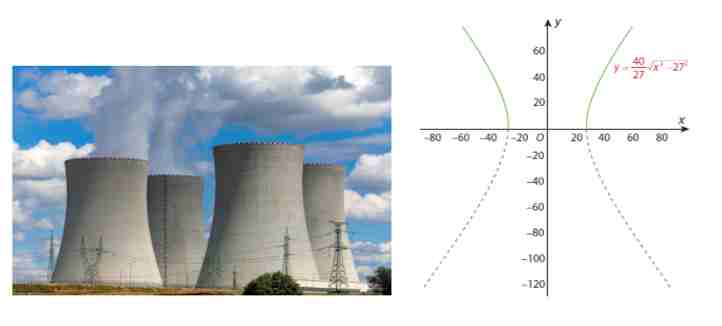
Xét hai nhánh bên trên Ox của (H) là đồ thị (C) của hàm số $\frac{x^2}{27^2} – \frac{y^2}{40^2} = 1$ (phần nét liền đậm). Đường thẳng $y = ax + c$ $(a > 0)$ là một đường tiệm cận xiên của (C). Tính tổng $T = 81a + c$.
Câu 4. Tập hợp tất cả các giá trị của tham số $m$ để hàm số $y = -x^3 – 6x^2 + (4m – 9)x + 4$ nghịch biến trên khoảng $\mathbb{R}$ là $\left(-\infty; \frac{a}{b}\right)$. Tính giá trị của $T = a + 2b$.
Câu 5. Cho hàm số $f(x) = 2x^3 – 9x^2 + mx$ với $m$ là tham số. Có bao nhiều số nguyên $m \leq 2025$ để $\max_{[0;3]} f(x) = f(3)$.
Câu 6. Một người ghi lại thời gian đàm thoại của một số cuộc gọi cho kết quả như bảng sau:

Tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên ?

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh

