PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.

Câu 1. Tìm nguyên hàm $\int(-x^2 – x – 3)dx$.

A. $-x^3 – x^2 – 3 + C$

B. $-\frac{x^3}{3} – \frac{x^2}{2} – 3x + C$

C. $-x^3 – x^2 – 3x + C$

D. $-\frac{x^3}{3} – x^2 – 3x + C$

Câu 2. Tìm nguyên hàm $\int(3\sin x + 4\cos x)dx$.

A. $3x + 4\sin x – 3\cos x + C$

B. $-4\sin x + 3\cos x + C$

C. $4\sin x – 3\cos x + C$

D. $-12\sin x + 9\cos x + C$

Câu 3. Tìm một nguyên hàm $F(x)$ của hàm số $f(x) = x^4 – 3x^3 – 4x^2 – 3x – 4$ biết $F(-6) = -\frac{11336}{5}$.

A. $F(x) = \frac{x^5}{5} – \frac{3x^4}{4} – \frac{4x^3}{3} – \frac{3x^2}{2} – 4x – 2$

B. $F(x) = \frac{x^5}{5} – \frac{3x^4}{4} – \frac{4x^3}{3} – \frac{3x^2}{2} – 4x + 2$

C. $F(x) = \frac{x^5}{5} – \frac{3x^4}{4} – \frac{4x^3}{3} + \frac{3x^2}{2} – 4x + 2$

D. $F(x) = \frac{x^5}{5} – \frac{3x^4}{4} – \frac{4x^3}{3} – \frac{3x^2}{2} – x – 10$

Câu 4. Biết $F(x)$ là một nguyên hàm của $f(x)$ thỏa mãn $\int_1^7 f(x)dx = -12, F(1) = -2$. Tính $F(7)$.

A. -14

B. -10

C. 10

D. 24

Câu 5. Cho $\int_5^{18} f(x)dx = 20$, $\int_8^{17} f(x)dx = -16$. Tính $\int_5^8 f(x)dx + \int_{17}^{18} f(x)dx$.

A. -320

B. 36

C. -36

D. 4

Câu 6. Tính tích phân $\int_4^7 (-3x – 4)dx$.

A. $-\frac{135}{2}$

B. $-\frac{117}{2}$

C. -45

D. $-\frac{123}{2}$

Câu 7. Cho hình phẳng giới hạn bởi đồ thị hàm số $y = 3x + 9$, trục hoành và các đường thẳng $x = -6, x = -4$. Tính thể tích khối tròn xoay tạo thành khi cho hình phẳng đó quay quanh trục $Ox$.

A. $84\pi$

B. $78\pi$

C. $82\pi$

D. $81\pi$

Câu 8. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = 6x^2 – 30x + 36$, trục $Ox$ và các đường thẳng $x = 2, x = 3$.

A. 175

B. 1

C. 4

D. 80

Câu 9. Trong không gian $Oxyz$, cho mặt phẳng $(R)$ có phương trình $8x + 23y – 20z – 70 = 0$. Điểm nào sau đây không thuộc mặt phẳng $(R)$?

A. $D(6; -3; -5)$

B. $N(1; -3; -7)$

C. $C(-3; 1; -4)$

D. $M(-7; -7; -5)$

Câu 10. Trong không gian $Oxyz$, cho mặt phẳng $(R): -7x + 6y + 7z – 7 = 0$ và mặt phẳng $(\gamma): -14x + 12y + 14z – 8 = 0$. Khoảng cách giữa hai mặt phẳng đã cho bằng

Câu 11. Một vật chuyển động với tốc độ $v(t) = 10t + 10$ (m/s), với thời gian $t$ tính bằng giây. Tính quãng đường vật đi được trong khoảng thời gian từ $t = 2$ đến $t = 4$.

A. $\frac{9800}{3}$ (m)

B. 20 (m)

C. 83 (m)

D. 80 (m)

Câu 12. Tính thể tích $V$ của phần vật thể giới hạn bởi hai mặt phẳng $x = 0$ và $x = 5$, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục $Ox$ tại điểm có hoành độ $x$ $(0 \leq x \leq 5)$ thì được thiết diện là một hình chữ nhật có hai cạnh là $7x$ và $\sqrt{25 – x^2}$.

A. $\frac{887}{3}\pi$

B. $\frac{875}{3}$

C. $\frac{59981}{5}\pi$

D. $\frac{59976}{5}$

PHẦN II. Câu trắc nghiệm đúng sai.

Câu 1. Cho $F(x)$ là một nguyên hàm của $f(x) = -2x – 1$. Xét tính đúng-sai của các khẳng định sau.

a) $F'(x) = -2$.

b) $\int_{-2}^2 (-2x – 1)dx = F(2) + F(-2)$.

c) $F(x) = x^2 – x + c$.

d) $\int_{-9}^{-5} f(x)dx = 52$.

Câu 2. Trong không gian $Oxyz$, cho mặt phẳng $(\alpha)$ có phương trình $x + 2y – z – 2 = 0$. Xét tính đúng-sai của các khẳng định sau

a) $\overrightarrow{n} = (-2; -4; 2)$ là một véctơ pháp tuyến của $(\alpha)$.

b) Điểm $B(3; -3; -5)$ không thuộc mặt phẳng $(\alpha)$.

c) Khoảng cách từ điểm $A(-7; -1; -4)$ đến mặt phẳng $(\alpha)$ bằng $\frac{7\sqrt{6}}{6}$.

d) Góc giữa mặt phẳng $(\alpha)$ và mặt phẳng $(R): 3x – 3y – 5z + 2 = 0$ bằng $82,8°$.

PHẦN III. Câu trắc nghiệm trả lời ngắn.

Câu 1. Trong không gian $Oxyz$, cho mặt phẳng $(R)$ có phương trình $-x + 6y + 7z + 34 = 0$. Mặt phẳng $(P)$ đi qua điểm $E(3; -3; -2)$ và song song với $(R)$ có phương trình dạng $-1x + ay + bz + c = 0$. Tính $a + b + c$.

Câu 2. Trong không gian $Oxyz$, cho mặt phẳng $(\beta): x + 3y – 5z – 4 = 0$ và điểm $A(1; 5; -5)$. Biết $G(a; b; c)$ là điểm đối xứng với điểm $A$ qua mặt phẳng $(\beta)$. Tính $a + b + c$ (kết quả làm tròn đến hàng phần mười).

Câu 3. Biết tích phân $\int_{-5}^0 [m(-4x – 2) + x^2 – 6x – 2)]dx = 8$. Giá trị của $m$ bằng (kết quả làm tròn đến hàng phần mười)

Câu 4. Tính thể tích $V$ của phần vật thể giới hạn bởi hai mặt phẳng $x = 0$ và $x = 6$, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục $Ox$ tại điểm có hoành độ $x$ $(0 \leq x \leq 6)$ thì được thiết diện là một hình chữ nhật có hai cạnh là $6x$ và $\sqrt{36 – x^2}$.

A. $435\pi$

B. $\frac{135833}{5}\pi$

C. $\frac{135828}{5}$

D. 432

PHẦN IV. Tự luận.

Câu 1. Tại một nhà máy, gọi $C(x)$ là tổng chi phí (tính theo triệu đồng) để sản xuất $x$ tấn sản phẩm $Z$ trong một tháng. Khi đó, đạo hàm $C'(x)$, gọi là chi phí cận biên, cho biết tốc độ tăng tổng chi phí theo lượng sản phẩm được sản xuất. Giả sử chi phí cận biên (tính theo triệu đồng trên tấn) của nhà máy được ước lượng bởi công thức $C'(x) = 11 – 0.10x + 0.00050x^2$ với $0 \leq x \leq 101$. Biết rằng $C(0) = 24$ triệu đồng, gọi là chi phí cố định. Tính tổng chi phí khi nhà máy sản xuất 93 tấn sản phẩm $Z$ trong tháng (kết quả làm tròn đến hàng đơn vị).

Câu 2. Một phần sàn trượt được định vị bởi các điểm $A, B, C, D$, như hình vẽ:

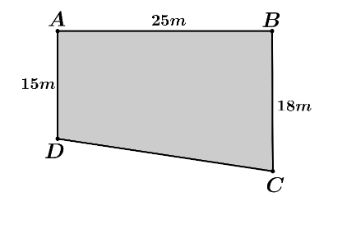
Bước đầu chúng được lấy “thẳng băng” để có cùng độ cao, biết $ABCD$ là hình thang vuông ở $A$ và $B$ với độ dài $AB = 25$m, $AD = 15$m, $BC = 18$m. Do yêu cầu kĩ thuật, khi lắp phẳng phần sàn trượt phải thoát nước về góc sàn ở $C$ nên người ta lấy độ cao ở các điểm $B$, $C$, $D$ xuống thấp hơn so với độ cao ở $A$ là $10$cm, $4$cm, $6$cm tương ứng. Giá trị của $a$ bằng bao nhiêu?

Câu 3. Mặt cắt của một cửa hầm có dạng là hình phẳng giới hạn bởi một parabol và đường thẳng nằm ngang như hình sau. Tính diện tích của cửa hầm.

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh