PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1: Hàm số $f(x)$ có nguyên hàm trên $K$ nếu:

A. $f(x)$ xác định trên $K$

B. $f(x)$ có giá trị lớn nhất trên $K$

C. $f(x)$ có giá trị nhỏ nhất trên $K$

D. $f(x)$ liên tục trên $K$

Câu 2: Họ nguyên hàm của hàm số $f(x) = x^{2025}$ là

A. $2026x^{2026} + C$

B. $2026x^{2025} + C$

C. $\frac{1}{2025}x^{2026} + C$

D. $\frac{1}{2026}x^{2026} + C$

Câu 3: Cho hai hàm số $f(x)$, $g(x)$ liên tục trên đoạn $[a; b]$ và số thực $k$. Trong các khẳng định sau, khẳng định nào sai?

A. $\int_a^b [f(x) + g(x)]dx = \int_a^b f(x)dx + \int_a^b g(x)dx$

B. $\int_a^b [f(x).g(x)]dx = \int_a^b f(x)dx.\int_a^b g(x)dx$

C. $\int_a^b [f(x) – g(x)]dx = \int_a^b f(x)dx – \int_a^b g(x)dx$

D. $\int_a^b kf(x)dx = k\int_a^b f(x)dx$

Câu 4: [Mức độ 2] Biết $F(x) = x^2$ là một nguyên hàm của hàm số $f(x)$ trên $\mathbb{R}$. Giá trị của $\int_1^3 [2 + f(x)]dx$ bằng

A. 3

B. 5

C. $\frac{13}{3}$

D. $\frac{7}{3}$

Câu 5: [Mức độ 1] Tính tích phân $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos x dx$.

A. 2

B. 0

C. -2

D. 1

Câu 6: [Mức độ 1] Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số $y = f(x)$, trục hoành và hai đường thẳng $x = a$, $x = b$ $(a < b)$ tính theo công thức nào dưới đây?

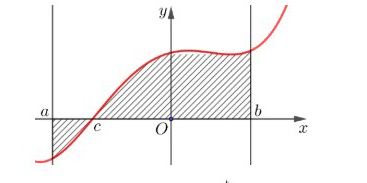
A. $S = \int_a^c f(x)dx + \int_c^b f(x)dx$

B. $S = \int_a^b f(x)dx$

C. $S = -\int_a^c f(x)dx + \int_c^b f(x)dx$

D. $S = \int_a^b |f(x)|dx$

Câu 7: Cho hình phẳng $D$ giới hạn bởi đường cong $y = \sqrt{2 + \cos x}$, trục hoành và các đường thẳng $x = 0, x = \frac{\pi}{2}$. Khối tròn xoay tạo thành khi quay $D$ quanh trục hoành có thể tích $V$ bằng bao nhiêu?

A. $V = \pi – 1$

B. $V = (\pi – 1)\pi$

C. $V = (\pi + 1)\pi$

D. $V = \pi + 1$

Câu 8: Trong không gian $Oxyz$, phương trình nào dưới đây là phương trình mặt phẳng $(P)$ đi qua điểm $M(1; 2; -3)$ và có một vector pháp tuyến $\overrightarrow{n} = (1; -2; 3)$?

A. $x – 2y + 3z – 12 = 0$

B. $x – 2y – 3z + 6 = 0$

C. $x – 2y + 3z + 12 = 0$

D. $x – 2y – 3z – 6 = 0$

Câu 9: Trong không gian $Oxyz$, cho điểm $M(2; -1; 1)$, tìm tọa độ $M’$ là hình chiếu vuông góc của $M$ trên mặt phẳng $(Oxy)$.

A. $M'(2; 1; 0)$

B. $M'(2; 1; -1)$

C. $M'(0; 0; 1)$

D. $M'(2; -1; 0)$

Câu 10: Trong không gian với hệ tọa độ $Oxyz$, mặt phẳng $(P)$ chứa hai điểm $A(1; 0; 3)$, $B(-1; 2; 2)$ và song song với trục $Ox$ có phương trình là

A. $3x – y + z = 1$

B. $y + 2z – 1 = 0$

C. $x – 2y + z – 1 = 0$

D. $y + 2z – 6 = 0$

Câu 11: Đường thẳng $d: \frac{x-1}{2} = \frac{y-3}{-1} = \frac{z+5}{3}$ có một vector chỉ phương là:

A. $\overrightarrow{u_1} = (2; 1; -3)$

B. $\overrightarrow{u_2} = (2; -1; 3)$

C. $\overrightarrow{u_3} = (2; 1; 3)$

D. $\overrightarrow{u_4} = (-2; -1; 3)$

Câu 12: Trong không gian với hệ tọa độ $Oxyz$, đường thẳng đi qua điểm $A(4; 0; -1)$ và vuông góc với mặt phẳng $(P): x – y + 3z + 2 = 0$ có phương trình tham số là

A. $\begin{cases} x = 4 + t \ y = -t \ z = -1 + 3t \end{cases}$

B. $\begin{cases} x = 1 + 4t \ y = -1 \ z = 3 – t \end{cases}$

C. $\begin{cases} x = 4t \ y = -t \ z = 3 + 2t \end{cases}$

D. $\begin{cases} x = 4 + t \ y = -t \ z = 1 – 3t \end{cases}$

PHẦN II. Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Mệnh đề đúng hay sai?

a) Nếu $f(x)$, $g(x)$ là hai hàm số liên tục trên $K$ thì $\int [f(x) – g(x)]dx = \int f(x)dx – \int g(x)dx$

b) Hàm số $F(x) = 2\sin x – 3\cos x$ là một nguyên hàm của hàm số $f(x) = 2\cos x – 3\sin x$ trên $\mathbb{R}$

c) Cho $\int_{-3}^0 f(x)dx = -4$ và $\int_{-3}^0 g(x)dx = -3$. Ta có $\int_{-3}^0 [2f(x) + 3g(x)]dx = -51$

d) Tính $I = \int_0^\frac{\pi}{4} (3 – \sin x)dx = a\pi – \frac{b}{c}$ (trong đó $a, b, c \in \mathbb{N}^*$ và $c$ là phân số tối giản). Ta có $c = a + b$.

Câu 2: [Mức độ 1-2-2-1] Cho hàm số $y = f(x) = x^3 – 3x + 2$ có đồ thị là $(C)$. Gọi $D$ là hình phẳng giới hạn bởi đồ thị $(C)$ và trục $Ox$. Xét tính đúng sai của các khẳng định sau:

a. [Mức độ 1] Diện tích hình phẳng $(D)$ là $S = \int_1^2 |x^3 – 3x + 2|dx$.

b. [Mức độ 2] Gọi $S’$ là diện tích hình phẳng giới hạn bởi đồ thị $(C)$, đường thẳng $(d): y = -2x + 8$ và 2 đường thẳng $x = 1; x = 3$. Khi đó $S’ = \frac{23}{2}$.

c. [Mức độ 2] Thể tích khối tròn xoay sinh ra khi quay hình phẳng $(D)$ quanh trục $Ox$ bằng $16\pi$

d. [Mức độ 3] Đường thẳng $x = k$ chia hình phẳng $(D)$ thành hai phần có diện tích bằng nhau. Khi đó $k \in (-1; 0)$

Câu 3: [NB-TH-TH-VD] Trong không gian $(Oxyz)$ cho ba điểm $A(1; 2; 3); B(-2; 1; 4); C(0; -1; 1)$. Gọi $(\alpha)$ là mặt phẳng đi qua điểm $A$ vuông góc với $AB$. Các khẳng định sau đúng hay sai.

a) Mặt phẳng $(\alpha)$ có một vector pháp tuyến $\overrightarrow{n} = (3; 1; -1)$.

b) Mặt phẳng $(\alpha)$ có phương trình dạng $ax + by + cz + 2 = 0$ với $a + b + c = 3$.

c) Khoảng cách từ $C$ đến mặt phẳng $(\alpha)$ là $\frac{2\sqrt{11}}{11}$.

d) Gọi $M$ là điểm nằm trên mặt phẳng $(\alpha)$, khi đó GTNN của $MB + MC$ là $\sqrt{33}$.

Câu 4: Trong không gian với hệ trục tọa độ $Oxyz$, cho đường thẳng $d: \frac{x+4}{3} = \frac{y-5}{-4} = \frac{z+2}{1}$.

a) Điểm $A(3; -4; 1)$ nằm trên đường thẳng $d$.

b) Một vector chỉ phương của $d$ là $\overrightarrow{u} = (-6; 8; -2)$

c) Đường thẳng $d$ song song với đường thẳng $\Delta: \begin{cases} x = -4 + 3s \ y = 5 – 4s \ z = -2 + s \end{cases}$.

d) Đường thẳng $\Delta$ song song với đường thẳng $d$, cắt cả hai đường thẳng $d_1: \frac{x-1}{3} = \frac{y+1}{-1} = \frac{z-2}{2}$ và $d_2: \frac{x+2}{2} = \frac{y-3}{-4} = \frac{z}{1}$ có phương trình là $\frac{x+4}{3} = \frac{y+1}{-4} = \frac{z+1}{1}$.

PHẦN III. Câu trắc nghiệm trả lời ngắn.

Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: [Mức độ 2] Cho $F(x) = (ax^2 + bx + c)e^{2x}$ là một nguyên hàm của hàm số $f(x) = (2x^2 + 6x)e^{2x}$. Tính tổng $a + b + 2c$.

Câu 2: [Mức độ 2] Trong không gian với hệ tọa độ $Oxyz$, cho hai mặt phẳng $(P): x + y + z – 3 = 0$, $(Q): x – y + z – 1 = 0$. Có bao nhiêu mặt phẳng $(R)$ vuông góc với cả $(P)$ và $(Q)$ sao cho khoảng cách từ điểm $O$ đến mặt phẳng $(R)$ bằng $\sqrt{2}$?

Câu 3: [Mức độ 3] Bạn An có các tấm thẻ hình chữ nhật có kích thước khác nhau nhưng có cùng chu vi là 6 cm. Trên mỗi tấm thẻ, An vẽ một hình parabol sao cho đỉnh của parabol trùng với trung điểm một cạnh của thẻ và hai điểm của hình chữ nhật như hình vẽ. Diện tích của hình parabol lớn nhất mà An có thể vẽ được bằng bao nhiêu cm²?

Câu 4: [Mức độ 3] Một chiếc cối giã bằng đá có hình dạng khối tròn xoay bên ngoài là hình nón cụt, cao 32cm. Cắt chiếc cối bởi mặt phẳng đi qua tâm của đáy và vuông góc với đáy ta thu được mặt cắt như hình dưới đây.

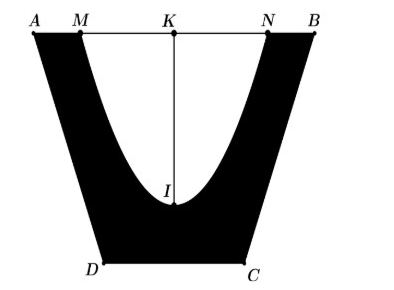
Biết rằng đường cong bên trong mặt cắt là một một phần của parabol có đỉnh $I$; $AB = 32cm$, $CD = 16cm$, $MN = 24cm$ và $IK = 24cm$. Thể tích phần đá của chiếc cối gần nhất với giá trị nào sau đây (tính theo đơn vị $cm^3$ và làm tròn đến hàng đơn vị)?

Câu 5: Trong không gian với hệ tọa độ $Oxyz$, cho đường thẳng $d: \frac{x-2}{1} = \frac{y}{-1} = \frac{z+2}{2}$ và mặt phẳng $(\alpha): 2x + 2y – z – 4 = 0$. Tam giác $ABC$ cân tại $A$ có $A(-1; 2; 1)$, các đỉnh $B, C$ nằm trên mặt phẳng $(\alpha)$ và trọng tâm $G$ nằm trên đường thẳng $d$. Đường thẳng $BC$ nhận $\overrightarrow{u}(a; b; 1)$ là một vector chỉ phương. Tính tổng $2a + b$.

Câu 6: Trong không gian ba chiều $Oxyz$, tọa độ các khu vực được xác định như sau:

Khu vực $A(30; 20; 0)$ nằm trên mặt đất, cách trung tâm thành phố 3km.

Khu vực $B(70; 50; 40)$ nằm trên tòa nhà cao tầng và ở độ cao 40m.

Khu vực $C(50; 80; 70)$ nằm trên một đỉnh đồi ở độ cao 70m.

Gọi vị trí lắp đặt trạm phát sóng là $D(a; b; c)$ sao cho khoảng cách từ $D$ đến ba khu vực kể trên là bằng nhau và khoảng cách đến chúng là nhỏ nhất. Tính $T = a + b + c$ (Kết quả làm tròn đến hàng đơn vị)