PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.

Câu 1: Trong không gian với hệ tọa độ $Oxyz$, cho hai mặt phẳng $(P): 2x + my + 3z – 5 = 0$ và $(Q): nx – 8y – 6z + 2 = 0$, với $m, n \in \mathbb{Z}$. Tìm $m, n$ để $(P)$ song song với $(Q)$.

A. $m = n = -4$.

B. $m = -4; n = 4$.

C. $m = 4; n = -4$.

D. $m = n = 4$.

Câu 2: Cho hai tích phân $\int_{-2}^5 f(x)dx = 8$ và $\int_5^{-2} g(x)dx = 3$. Tính $I = \int_{-2}^5 [f(x) – 4g(x) – 1]dx$.

A. $13$.

B. $27$.

C. $-11$.

D. $3$.

Câu 3: Trong không gian với hệ tọa độ $Oxyz$, cho ba điểm $A(2; -1; 3), B(2; 0; 5), C(0; -3; -1)$. Phương trình nào dưới đây là phương trình của mặt phẳng đi qua $A$ và vuông góc với $BC$?

A. $x – y + 2z + 9 = 0$.

B. $x – y + 2z – 9 = 0$.

C. $2x + 3y – 6z – 19 = 0$.

D. $2x + 3y + 6z – 19 = 0$.

Câu 4: Cho $f(x)$ là hàm số liên tục trên đoạn $[a; b]$. Giả sử $F(x), G(x)$ là các nguyên hàm của $f(x)$ trên đoạn $[a; b]$. Trong các phát biểu sau, phát biểu nào sai?

A. $F(a) – F(b) = G(a) – G(b)$.

B. $\int_a^b f(x)dx = F(b) – F(a)$.

C. $\int_a^b f(x)dx = f(b) – f(a)$.

D. $\int_a^b f(x)dx = G(b) – G(a)$.

Câu 5: Cho các hàm số $f(x), g(x)$ liên tục trên $\mathbb{R}$ và $k$ là một số thực. Trong các khẳng định nào sau đây là đúng?

A. $\int f(x).g(x)dx = \int f(x)dx.\int g(x)dx$.

B. $\int [f(x) – g(x)]dx = \int f(x)dx – \int g(x)dx$.

C. $\int k.f(x)dx = f(kx) + C$.

D. $\int k.f(x)dx = k\int f(x)dx$.

Câu 6: Tìm họ nguyên hàm của hàm số $f(x) = 2024\sin x + 2025\cos x$.

A. $2024\cos x + 2025\sin x + C$.

B. $2024\cos x – 2025\sin x + C$.

C. $-2024\cos x – 2025\sin x + C$.

D. $-2024\cos x + 2025\sin x + C$.

Câu 7: Biết $F(x) = x^4 – \frac{2}{3}x^3 – 5$ là một nguyên hàm của hàm số $f(x)$. Hãy tính $f(-1)$.

A. $f(-1) = -6$.

B. $f(-1) = -\frac{14}{3}$.

C. $f(-1) = \frac{151}{30}$.

D. $f(-1) = -2$.

Câu 8: Mặt phẳng $(ABC)$ có $A(2; -1; 3), B(1; -3; 0), C(3; 4; 2)$ có một vector pháp tuyến có tọa độ?

A. $\vec{n} = (17; 4; -3)$.

B. $\vec{n} = (-17; 4; -3)$.

C. $\vec{n} = (17; -4; 3)$.

D. $\vec{n} = (17; -4; -3)$.

Câu 9: Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A(1; -3; 2), B(3; 5; -2)$. Viết phương trình mặt phẳng trung trực của đoạn thẳng $AB$.

A. $x – 4y – 2z – 6 = 0$.

B. $x + 4y – 2z – 6 = 0$.

C. $x + 4y + 2z – 6 = 0$.

D. $x + 4y – 2z + 6 = 0$.

Câu 10: Trong không gian với hệ tọa độ $Oxyz$, cho ba mặt phẳng $(P): x + y + z – 1 = 0$, $(Q): 2x + my + 2z + 3 = 0$ và $(R): -x + 2y + nz = 0$. Tìm tổng $m + 2n$, biết rằng $(P) \perp (R)$ và $(P) // (Q)$.

A. $6$.

B. $1$.

C. $0$.

D. $-6$.

Câu 11: Trong không gian $Oxyz$, phương trình của mặt phẳng $(P)$ song song với mặt phẳng $(Q): x + 2y + z – 10 = 0$ và cách điểm $M(1; 0; 3)$ một khoảng bằng $\sqrt{6}$ là

A. $x + 2y + z + 2 = 0$ hoặc $x + 2y + z – 10 = 0$.

B. $x + 2y + z + 10 = 0$.

C. $x + 2y + z – 2 = 0$ hoặc $x + 2y + z + 10 = 0$.

D. $x + 2y + z + 2 = 0$.

Câu 12: Tìm thể tích $V$ của vật thể nằm giữa hai mặt phẳng $x = 0$, $x = \frac{\pi}{4}$ biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục $Ox$ tại điểm có hoành độ $x\left(0 \leq x \leq \frac{\pi}{4}\right)$ là tam giác đều có cạnh là $2\sqrt{\cos x – \sin x}$.

A. $2\sqrt{3}$.

B. $\sqrt{3}\left(\sqrt{2} – 1\right)$.

C. $\sqrt{3}$.

D. $2\pi\sqrt{3}$.

PHẦN II. Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S).

Câu 1: Cho số thực $a$ và hàm số

a) [NB] $\int_{-1}^0 f(x)dx = \int_{-1}^0 2x dx$.

b) [TH] $\int_0^1 f(x)dx = -\frac{a}{6}$.

c) [TH] Khi $a = 2$, $\int_{-1}^1 f(x)dx = -\frac{2}{3}$.

d) [VD] Điều kiện cần và đủ để $\int_{-1}^a f(x)dx > 3$ là $a > -6$.

Câu 2: Cho mặt phẳng $(P): 2x – y – 3 = 0$ và hai điểm $A(1; 0; 3), B(-1; 4; 2)$.

a) [NB] Mặt phẳng $(P): 2x – y – 3 = 0$ đi qua gốc tọa độ.

b) [TH] Vector pháp tuyến của mặt phẳng $(P): 2x – y – 3 = 0$ là $\vec{n}(2; -1; -3)$.

c) [TH] Mặt phẳng $(P): 2x – y – 3 = 0$ vuông góc với mặt phẳng $(Q): x + 2y + 1 = 0$.

d) [VD] Phương trình mặt phẳng $(\alpha)$ đi qua hai điểm $A, B$ và vuông góc với mặt phẳng $(P)$ có phương trình dạng $ax + y + bz + c = 0$. Khi đó $a + b + c = -6$.

Câu 3: Cho hàm số $F(x) = \int \sqrt{x}(x^2 – 5x + 1)dx = \frac{ax^3\sqrt{x}}{b} – ax^2\sqrt{x} + \frac{a}{c}x\sqrt{x} + C(x > 0)$. Xét tính đúng sai của các khẳng định sau.

a) $F(x) = \frac{2x^3\sqrt{x}}{7} – 2x^2\sqrt{x} + \frac{2}{3}x\sqrt{x} + C$.

b) Tổng $a + b + c = 12$.

c) Tích $abc = 42$.

d) Nếu $F(1) = \frac{2002}{21}$ thì $F(x) = \frac{2x^3\sqrt{x}}{7} – 2x^2\sqrt{x} + \frac{2}{3}x\sqrt{x} + 2024$.

Câu 4: Một cánh cổng của một tòa nhà có dạng parabol gồm hai phần: phần hai cánh của hình chữ nhật $CDEF$, còn lại là phần xiên hoa trang trí. Biết rằng $GH = 4$ m, $AB = 4$ m và $AC = BD = 0,9$ m.

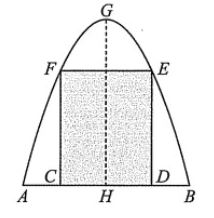
Chọn hệ trục tọa độ $Oxy$ sao cho $AB$ trùng $Ox$, $A$ trùng $O$.

a) [NB] Khi đó parabol có đỉnh $G(2; 4)$.

b) [TH] Khi đó parabol có phương trình $f(x) = -x^2 + 4x$.

c) [TH] Diện tích của cánh cổng là $\frac{29}{3}$ m².

d) [VD] Diện tích phần xiên hoa trang trí xấp xỉ $3,53$ m².

PHẦN III. Câu trắc nghiệm trả lời ngắn.

Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: Người thợ gốm làm cái chum từ một khối cầu có bán kính $15dm$ bằng cách cắt bỏ hai chóm cầu đối nhau. Chọn hệ trục tọa độ như hình vẽ.

Thể tích của cái chum có kết quả là $m\pi (dm^3)$, biết chiều cao của cái chum là $12dm$. Hãy tìm $m$?

Câu 2: Cho tứ diện $OABC$ có $OA, OB, OC$ đôi một vuông góc và $OA = 6, OB = 8, OC = 8$. Gọi $M, N$ lần lượt là trung điểm của $OB$ và $OC$. Gọi $G$ là trọng tâm của tam giác $ABC$. Khoảng cách từ $G$ đến mặt phẳng $(AMN)$ là $\frac{\sqrt{a}}{24}$. Tính $a$.

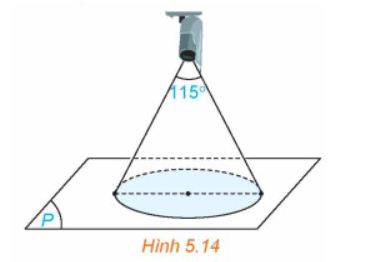
Câu 3: Góc quan sát ngang của một camera là $115°$. Trong không gian $Oxyz$, camera được đặt tại điểm $C(1; 2; 4)$ và chiếu thẳng về phía mặt phẳng $(P): x + 2y + 2z + 3 = 0$. Hỏi vùng quan sát được trên mặt phẳng $(P)$ của camera là hình tròn có bán kính bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ hai.)

Câu 4: Một vật được ném lên từ độ cao $300$ m với vận tốc được cho bởi công thức $v(t) = -9,8t + 31,3(m/s)$ (Nguồn: R.Larson and B. Edwards, Calculus 10e, Cengage). Gọi $h(t)(m)$ là độ cao của vật tại thời điểm $t(s)$. Sau bao lâu kể từ khi bắt đầu được ném lên thì vật đó chạm đất lần trước kết quả chỉ thập phân thứ nhất?

Câu 5: Một khối gỗ hình trụ với bán kính đáy bằng $3$ và chiều cao bằng $4$. Trên một đường tròn đáy nào đó ta lấy hai điểm $A$, $B$ sao cho cung $AB$ có số đo $60°$. Người ta cắt khúc gỗ bởi một mặt phẳng đi qua $A$, $B$ và tâm của hình trụ (tâm của hình trụ là trung điểm của đoạn nối tâm hai đáy) để được thiết diện như hình vẽ. Tính diện tích $S$ của thiết diện (làm tròn đến hàng đơn vị).

Câu 6: Biết $\int_1^4 \frac{\sqrt{x^2 – 6x + 9} – x}{x} dx = a \ln 2 + b \ln 3 + c$ với $a, b, c$ là các số nguyên. Tính tổng $P = a + b + c$.

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh