PHẦN I. Câu trắc nghiệm với nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn một phương án.

Câu 1: Trong không gian $Oxyz$, cho hai vectơ $\vec{a} = (-4; 5; -3)$, $\vec{b} = (2; -2; 1)$. Tìm tọa độ của vectơ $\vec{x} = \vec{a} + 2\vec{b}$.

A. $\vec{x} = (0; 1; 1)$.

B. $\vec{x} = (0; 1; -1)$.

C. $\vec{x} = (-8; 9; -5)$.

D. $\vec{x} = (2; 3; -2)$.

Câu 2: Cho hàm số $y = f(x)$ có bảng biến thiên như sau:

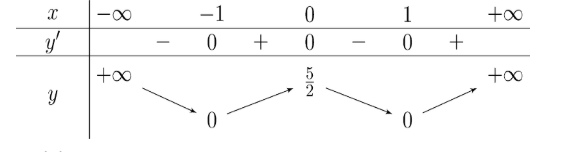
Hàm số $y = f(x)$ nghịch biến trên khoảng nào sau đây?

A. $(0; +\infty)$.

B. $(-\infty; 0)$.

C. $(-1; 0)$.

D. $(-\infty; -1)$.

Câu 3: Khi thống kê cân nặng (đơn vị: kilogram) của các học sinh lớp 12A, người ta sử dụng mẫu số liệu ghép nhóm và kết quả được cho bởi bảng sau

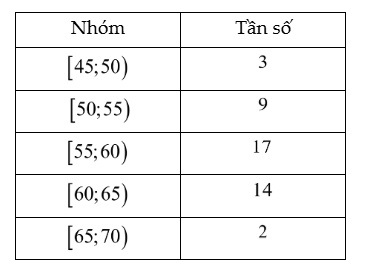
Khoảng biến thiên của mẫu số liệu ghép nhóm đó bằng:

A. 25.

B. 50.

C. 20.

D. 75.

Câu 4: Cho hình hộp $ABCD.A’B’C’D’$.

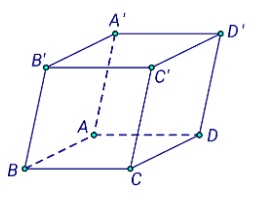
Khẳng định nào sau đây sai?

A. $\overrightarrow{AB} = \overrightarrow{D’C’}$.

B. $\overrightarrow{AB} + \overrightarrow{AD} = \overrightarrow{A’C’}$.

C. $\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA’} = \overrightarrow{AC’}$.

D. $\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{BB’} = \overrightarrow{A’C}$.

Câu 5: Trong không gian $Oxyz$, cho hai điểm $A(1; 2; -3)$ và $B(-3; 4; 5)$. Tìm điểm $I$ là trung điểm của đoạn thẳng $AB$.

A. $I(-1; 3; 1)$.

B. $I(-1; -3; 1)$.

C. $I(-2; 1; 4)$.

D. $I(2; -1; -4)$.

Câu 6: Cho hai vectơ $\vec{a}$ và $\vec{b}$ thỏa mãn $|\vec{a}| = 3$, $|\vec{b}| = 2$ và $\vec{a}.\vec{b} = -3$. Xác định góc $\alpha$ giữa hai vectơ $\vec{a}$ và $\vec{b}$.

A. $\alpha = 30°$.

B. $\alpha = 45°$.

C. $\alpha = 60°$.

D. $\alpha = 120°$.

Câu 7: Trong không gian $Oxyz$, cho ba vectơ $\vec{a} = (1; 2; 3)$, $\vec{b} = (-1; -3; 1)$, $\vec{c} = (2; -1; 4)$. Khi đó, vectơ $\vec{d} = (-3; -4; 5)$ phân tích theo ba vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$ là

A. $\vec{d} = 2\vec{a} + 3\vec{b} + \vec{c}$.

B. $\vec{d} = 2\vec{a} + 3\vec{b} – \vec{c}$.

C. $\vec{d} = \vec{a} + 3\vec{b} – \vec{c}$.

D. $\vec{d} = 2\vec{a} – 3\vec{b} – \vec{c}$.

Câu 8: Cho bảng số liệu về thời gian sử dụng điện thoại sau khi sạc đầy của chị An.

Hãy tính gần đúng thời gian sử dụng trung bình từ lúc chị An sạc đầy pin điện thoại cho tới khi hết pin.

A. 12 (giờ).

B. 12,2 (giờ).

C. 12,4 (giờ).

D. 12,3 (giờ).

Câu 9: Cho hàm số $y = f(x)$ có bảng biến thiên như sau:

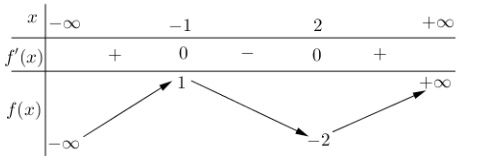
Giá trị cực tiểu của hàm số đã cho bằng

A. $-1$.

B. $2$.

C. $-2$.

D. $1$.

Câu 10: Cho tứ diện $ABCD$. Gọi $M$ và $P$ lần lượt là trung điểm của các cạnh $AB$ và $CD$. Đặt $\overrightarrow{AB} = \vec{b}$, $\overrightarrow{AC} = \vec{c}$, $\overrightarrow{AD} = \vec{d}$. Khẳng định nào sau đây đúng?

A. $\overrightarrow{MP} = \frac{1}{2}(\vec{c} + \vec{d} + \vec{b})$.

B. $\overrightarrow{MP} = \frac{1}{2}(\vec{d} + \vec{b} – \vec{c})$.

C. $\overrightarrow{MP} = \frac{1}{2}(\vec{c} + \vec{b} – \vec{d})$.

D. $\overrightarrow{MP} = \frac{1}{2}(\vec{c} + \vec{d} – \vec{b})$.

Câu 11: Trong không gian $Oxyz$, cho hai vectơ $\vec{a} = (1; 2; 0)$ và $\vec{b} = (-1; 3; 0)$. Tính góc giữa hai vectơ đó.

A. $45°$.

B. $135°$.

C. $30°$.

D. $60°$.

Câu 12: Điểm kiểm tra 15 phút của 36 học sinh lớp 11A được cho bởi bảng tần số ghép nhóm sau:

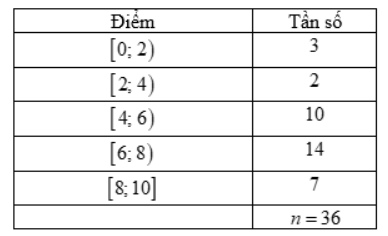
Độ lệch chuẩn của mẫu số liệu ghép nhóm (kết quả làm tròn đến hàng phần trăm) là

A. 2,24.

B. 2,23.

C. 2,2.

D. 2,32.

PHẦN II. Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Cho hàm số $y = f(x)$ có bảng biến thiên như sau:

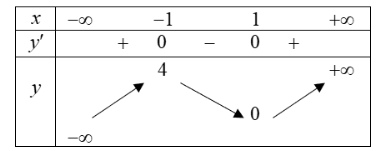
a) Giá trị cực đại của hàm số bằng 4.

b) $f(-25) > f(-24)$.

c) $\max_{x \in (-\infty; 1)} f(x) = f(-1)$.

d) Hàm số đồng biến trên $(-\infty; -1) \cup (1; +\infty)$.

Câu 2: Cho hình hộp chữ nhật $ABCD.A’B’C’D’$ có cạnh $AB = a$, $AD = a\sqrt{3}$, $AA’ = 2a$.

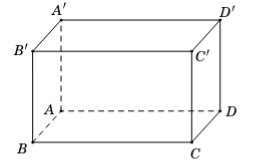
a) $\overrightarrow{AB’} + \overrightarrow{CD’} = \vec{0}$.

b) $\overrightarrow{A’D} + \overrightarrow{CB’} = \vec{0}$.

c) $|\overrightarrow{AB} + \overrightarrow{AD}| = a\sqrt{5}$.

d) $|\overrightarrow{AB} + \overrightarrow{A’D’} + \overrightarrow{CC’}| = 2\sqrt{2}a$.

Câu 3: Trong không gian $Oxyz$, cho tam giác $ABC$ có $A(3; 0; 0)$, $B(0; -2; 0)$ và $C(0; 0; -1)$.

a) Điểm $A$ thuộc trục hoành $Ox$.

b) $\overrightarrow{AB} = (-3; 2; 0)$.

c) Diện tích tam giác $OAB$ bằng 3.

d) Thể tích tứ diện $OABC$ bằng 1.

Câu 4: Hàng ngày ông Thắng đều đi xe buýt từ nhà đến cơ quan. Dưới đây là bảng thống kê thời gian của 100 lần ông Thắng đi xe buýt từ nhà đến cơ quan:

a) Cỡ mẫu $n = 100$.

b) Khoảng biến thiên của mẫu số liệu ghép nhóm là 15 phút.

c) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là $Q_1 = \frac{683}{38}$.

d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là $\Delta_Q = \frac{505}{114}$.

PHẦN III. Câu trắc nghiệm trả lời ngắn.

Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: Cho hàm số $y = \frac{ax + b}{x + c}$ ($a, b, c \in \mathbb{R}$) có đồ thị như hình bên dưới:

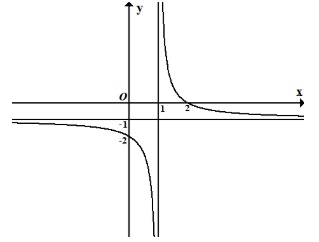
Tính giá trị của biểu thức $a – 3b + 2c$.

Câu 2: Trong không gian $Oxyz$, cho ba điểm $A(1; -1; 3)$, $B(2; -3; 5)$, $C(-1; -2; 6)$. Biết điểm $M(a; b; c)$ thỏa mãn $\overrightarrow{MA} + 2\overrightarrow{MB} – 2\overrightarrow{MC} = \vec{0}$, tính $a – b + c$.

Câu 3: Bạn Chi rất thích nhảy hiện đại. Thời gian tập nhảy mỗi ngày trong thời gian gần đây của bạn Chi được thống kê lại ở bảng sau:

Tính gần đúng đến hàng phần trăm phương sai của mẫu số liệu ghép nhóm trên.

Câu 4: Cho tứ diện $ABCD$, $O$ là trọng tâm tam giác $BCD$, $M$ là trung điểm của $AD$. Biết $\overrightarrow{OM} = a\overrightarrow{AB} + b\overrightarrow{AC} + c\overrightarrow{AD}$, tính $3a + b + 2c$.

Câu 5: Trong không gian $Oxyz$, cho hình vuông $ABCD$, $B(3; 0; 8)$, $D(-5; -4; 0)$. Biết đỉnh $A$ thuộc mặt phẳng $(Oxy)$, có tọa độ là những số nguyên và $C(a; b; c)$. Tính $a + b + c$.

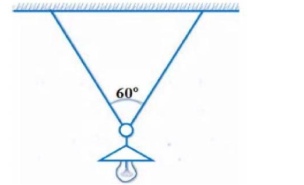
Câu 6: Người ta treo một bóng đèn có khối lượng $m = \sqrt{3}$ kg bằng cách luôn sợi dây qua một cái móc của đèn và hai đầu dây được gắn chặt trên trần nhà. Hai nửa sợi dây có chiều dài bằng nhau và hợp với nhau một góc bằng $60°$. Lực căng của mỗi nửa sợi dây là bao nhiều? Lấy $g = 10$ m/s².

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh