Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Cho hàm số $y = f(x)$ có đồ thị như hình dưới. Hàm số đã cho đồng biến trên khoảng nào trong các khoảng sau đây?
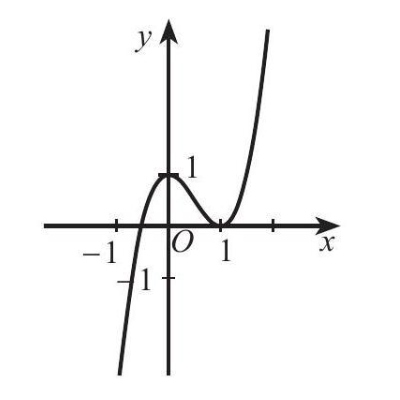
A. $(0; 1)$.
B. $(0; 2)$.
C. $(-1; 0)$.
D. $(-1; 1)$.
Câu 2. Cho hàm số $y = f(x)$ có đồ thị như hình. Hàm số đã cho có điểm cực đại là:
A. $1$.
B. $-1$.
C. $2$.
D. $-2$.
Câu 3. Cho hàm số $y = f(x)$ có đồ thị như hình. Giá trị nhỏ nhất của hàm số đã cho trên đoạn $[-1; 1]$ là:
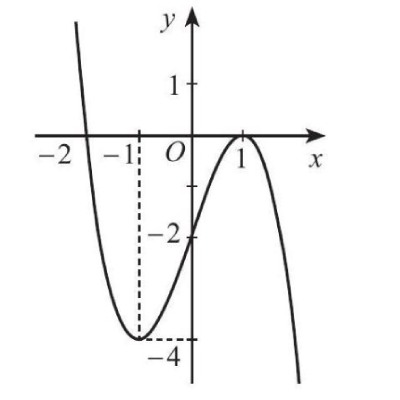
A. $-1$.
B. $1$.
C. $-4$.
D. $-2$.
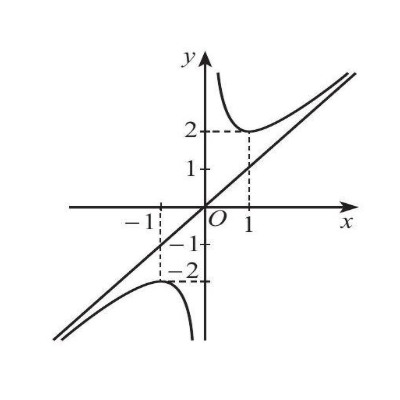
Câu 4. Cho hàm số $y = f(x)$ có đồ thị như hình. Đồ thị hàm số đã cho có đường tiệm cận ngang là:
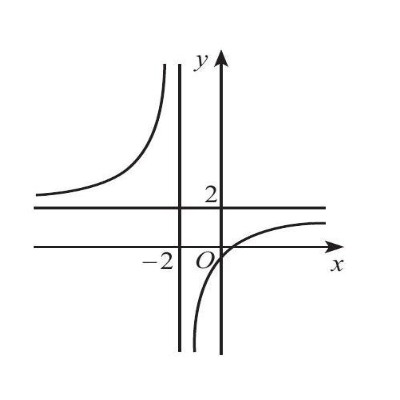
A. $x = -1$.
B. $y = -1$.
C. $x = 2$.
D. $y = 2$.
Câu 5. Cho hình hộp $ABCD.A’B’C’D’$ như hình. Phát biểu nào sau đây là đúng?
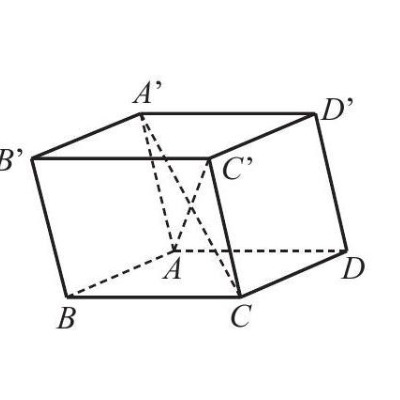
A. $\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA’} = \overrightarrow{CA’}$.
B. $\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA’} = \overrightarrow{C’A}$.
C. $\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA’} = \overrightarrow{A’C}$.
D. $\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA’} = \overrightarrow{AC’}$.
Câu 6. Trong không gian tọa độ $Oxyz$, tọa độ của vectơ $\vec{u} = 4\vec{i} – 5\vec{j} + 6\vec{k}$ là:
A. $(4; 5; 6)$.
B. $(4; -5; 6)$.
C. $(4; 5; -6)$.
D. $(-4; 5; 6)$.
Câu 7. Trong không gian tọa độ $Oxyz$, tích vô hướng của hai vectơ $\vec{u} = (x_1; y_1; z_1)$ và $\vec{b} = (x_2; y_2; z_2)$ bằng:
A. $x_1x_2 + y_1y_2 + z_1z_2$.
B. $(x_1 + x_2; y_1 + y_2; z_1 + z_2)$.
C. $\sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2 + (z_2 – z_1)^2}$.
D. $(x_1 + y_1 + z_1)(x_2 + y_2 + z_2)$.
Câu 8. Trong không gian tọa độ $Oxyz$, tổng của hai vectơ $\vec{a} = (x_1; y_1; z_1)$ và $\vec{b} = (x_2; y_2; z_2)$ là một vectơ có tọa độ là:
A. $(x_1x_2; y_1y_2; z_1z_2)$.
B. $(x_1 + x_2; y_1 + y_2; z_1 + z_2)$.
C. $(x_2 – x_1; y_2 – y_1; z_2 – z_1)$.
D. $(x_1 – x_2; y_1 – y_2; z_1 – z_2)$.
Câu 9. Trong không gian tọa độ $Oxyz$, khoảng cách giữa hai điểm $M(x_M; y_M; z_M)$ và $N(x_N; y_N; z_N)$ bằng:
A. $(x_M + x_N; y_M + y_N; z_M + z_N)$.
B. $\sqrt{(x_N – x_M)^2 + (y_N – y_M)^2 + (z_N – z_M)^2}$.
C. $(x_M + y_M + z_M)(x_N + y_N + z_N)$.
D. $x_Mx_N + y_My_N + z_Mz_N$.
Câu 10. Xét mẫu số liệu ghép nhóm cho bởi Bảng 1. Gọi $\bar{x}$ là số trung bình cộng của mẫu số liệu ghép nhóm đó. Độ lệch chuẩn của mẫu số liệu ghép nhóm được tính bằng công thức nào trong các công thức dưới đây?
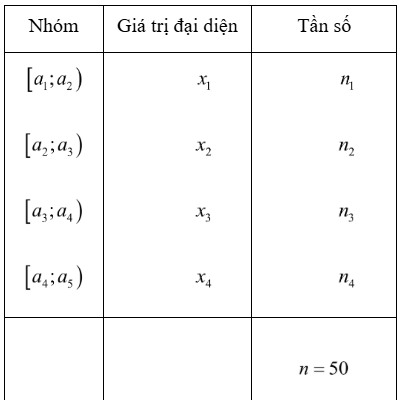
A. $s^2 = \frac{n_1(x_1 – \bar{x})^2 + n_2(x_2 – \bar{x})^2 + n_3(x_3 – \bar{x})^2 + n_4(x_4 – \bar{x})^2}{4}$.
B. $s = \sqrt{\frac{n_1(x_1 – \bar{x})^2 + n_2(x_2 – \bar{x})^2 + n_3(x_3 – \bar{x})^2 + n_4(x_4 – \bar{x})^2}{4}}$.
C. $s^2 = \frac{n_1(x_1 – \bar{x})^2 + n_2(x_2 – \bar{x})^2 + n_3(x_3 – \bar{x})^2 + n_4(x_4 – \bar{x})^2}{50}$.
D. $s = \sqrt{\frac{n_1(x_1 – \bar{x})^2 + n_2(x_2 – \bar{x})^2 + n_3(x_3 – \bar{x})^2 + n_4(x_4 – \bar{x})^2}{50}}$.
Câu 11. Cho tứ diện $ABCD$. Biểu thức $\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CD}$ bằng:
A. $\overrightarrow{AD}$.
B. $\overrightarrow{DA}$.
C. $\overrightarrow{BD}$.
D. $\overrightarrow{DB}$.
Câu 12. Khi thống kê cân nặng (đơn vị: kilogram) của các học sinh lớp 12 A, người ta sử dụng mẫu số liệu ghép nhóm và kết quả được cho bởi Bảng sau.

Khoảng biến thiên của mẫu số liệu ghép nhóm đó bằng:
A. 25.
B. 50.
C. 20.
D. 75.
PHẦN II. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số $f(x) = -x^3 + 3x$.
a) $f'(x) = -3x^2 + 3$.
b) Hàm số đồng biến trên các khoảng $(-\infty; -1)$ và $(1; +\infty)$; nghịch biến trên khoảng $(-1; 1)$.
c) Hàm số đạt cực tiểu tại $x_1 = -1$ và đạt cực đại tại $x_2 = 1$.
d) Hàm số có đồ thị như Hình 6.
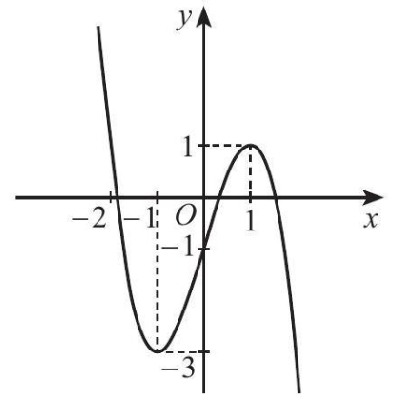
Câu 2. Cho hàm số $f(x) = e^x – x$.
a) $f'(x) = e^x + 1$.
b) $f'(x) = 0 \Leftrightarrow x = 0$.
c) Bảng biến thiên của hàm số $f(x)$ là:
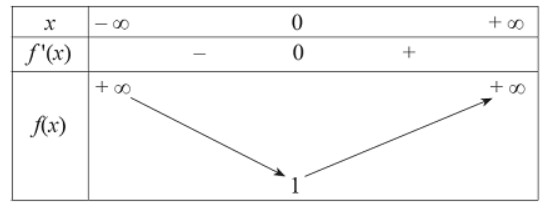
d) Giá trị nhỏ nhất của hàm số đã cho trên $\mathbb{R}$ là 1.
Câu 3. Một bệnh viện thống kê chỉ số đường huyết (đơn vị: milimol/lit) của 100 bệnh nhân. Số liệu được ghi lại trong Bảng 3.
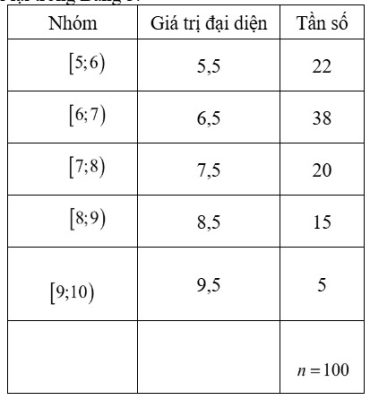
a) Số trung bình cộng của mẫu số liệu ghép nhóm được tính bằng biểu thức: $\bar{x} = \frac{22 \cdot 5,5 + 38 \cdot 6,5 + 20 \cdot 7,5 + 15 \cdot 8,5 + 5 \cdot 9,5}{100}$.
b) Số trung bình cộng của mẫu số liệu ghép nhóm là 6,93.
c) Phương sai của mẫu số liệu ghép nhóm là $s^2 = 1,2$.
d) Độ lệch chuẩn của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là 1,13.
Câu 4. Trong không gian tọa độ $Oxyz$, cho hai vectơ $\vec{u} = (-1; 2; 2)$ và $\vec{v} = (-3; -4; 0)$.
a) Nếu một vectơ có tọa độ là $(x; y; z)$ thì vectơ đó có độ dài là $\sqrt{x^2 + y^2 + z^2}$.
b) $|\vec{u}| = 3, |\vec{v}| = 5$.
c) $\vec{u} \cdot \vec{v} = 5$.
d) Góc giữa hai vectơ $\vec{u}$ và $\vec{v}$ (làm tròn đến hàng đơn vị của độ) là $81°$.
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Cho hàm số $y = x + \frac{1}{x}$ có bảng biến thiên như sau. Giá trị của biểu thức $S = a + 2b + 3c$ bằng bao nhiều?
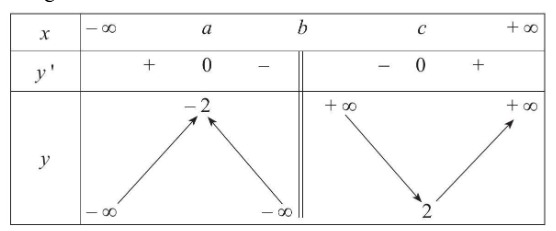
Câu 2. Trong không gian tọa độ $Oxyz$, cho $\vec{u} = (3; 4; -7), \vec{v} = (-1; 5; 8)$. Biết $2\vec{u} – 3\vec{v}$ có tọa độ là $(a; b; c)$. Giá trị của $a + b + c$ là bao nhiều?
Câu 3. Khi thống kê chiều cao của các học sinh nữ khối 12 ở một trường phổ thông, người ta tổng hợp kết quả (đơn vị: cm) bằng một mẫu số liệu ghép nhóm. Mẫu số liệu ghép nhóm có số trung bình là 156,3; tứ phân vị thứ nhất là 154,5; tứ phân vị thứ tư thi liệu là 8,166,3 và 170,2. Khoảng tứ phân vị của mẫu số liệu ghép nhóm đó bằng bao nhiều?
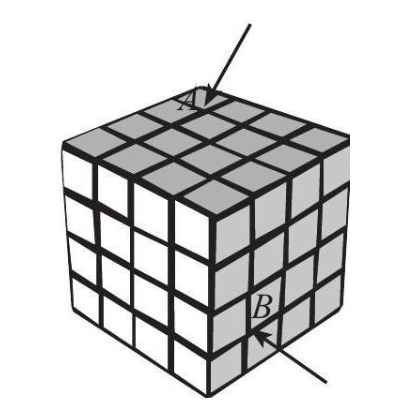
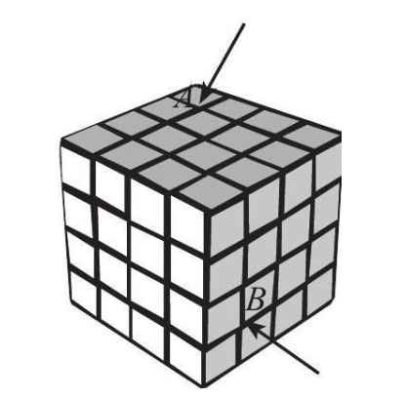
Câu 4. Một khối rubik có dạng $4 \times 4$ (mỗi cạnh của hình lập phương nhỏ nhất có độ dài 1 cm, mỗi cạnh của khối rubik gấp bốn lần cạnh hình lập phương nhỏ nhất đó). Xét hai vị trí $A$ và $B$, trong đó $A$ ở mặt trên cùng và $B$ ở mặt bên phải, với $A$ và $B$ đều là các đỉnh của khối lập phương nhỏ (Hình 7). Khoảng cách giữa hai điểm $A$ và $B$ bằng bao nhiều centimet (làm tròn kết quả đến hàng phần mười)?
Câu 5. Quynh có một tấm giấy màu có dạng nửa hình tròn bán kính 2dm. Quynh cắn cắt từ tấm giấy màu này ra một tấm giấy hình chữ nhật có một cạnh thuộc đường kính của nửa hình tròn (Hình 8) sao cho diện tích của tấm bìa được cắt ra là lớn nhất. Giá trị lớn nhất của diện tích
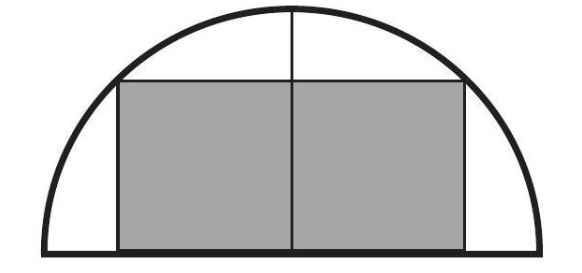
Câu 6. Bạn Dung cần gấp một hộp quà có dạng hình lăng trụ tứ giác đều với thể tích bằng 8dm³. Diện tích toàn phần của hộp quà đó có giá trị nhỏ nhất bằng bao nhiều decimet vuông?

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh