Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Cho hàm số $f(x)$ có bảng biến thiên như sau
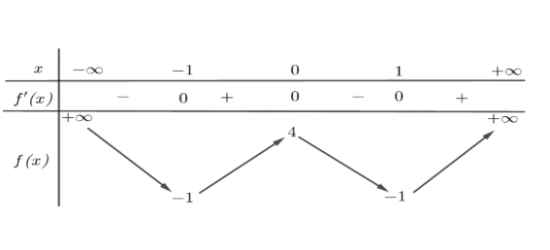
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. $(-\infty; -1)$.
B. $(0; 1)$.
C. $(-1; 1)$.
D. $(-1; 0)$.
Câu 2. Cho hàm số $f(x)$ có bảng biến thiên như sau
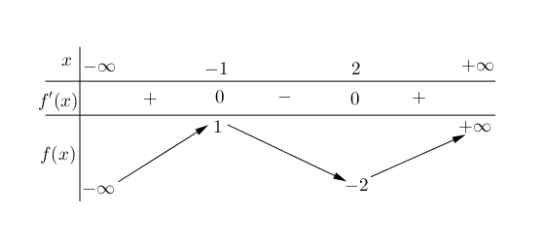
Hàm số đã cho đạt cực đại tại
A. $x = -2$.
B. $x = 2$.
C. $x = 1$.
D. $x = -1$.
Câu 3. Tiệm cận ngang của đồ thị hàm số $y = \frac{x-2}{x+1}$ là
A. $y = -2$.
B. $y = 1$.
C. $x = -1$.
D. $x = 2$.
Câu 4. Đường cong cho trong hình bên là đồ thị của hàm số nào trong các hàm số dưới đây?
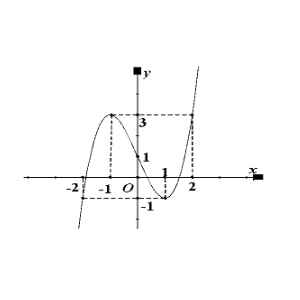
A. $y = -x^3 + 2x – 1$.
B. $y = -x^3 + 3x + 1$.
C. $y = 2x^3 – 6x + 1$.
D. $y = x^3 – 3x + 1$.
Câu 5. Đường cong cho trong hình bên là đồ thị của hàm số nào trong các hàm số dưới đây?
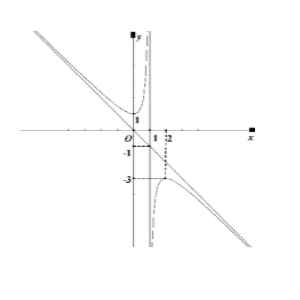
A. $y = \frac{x^2 – 2x + 2}{x + 1}$.
B. $y = \frac{-x^2 + x + 2}{x + 1}$.
C. $y = \frac{-x^2 + x – 1}{x – 1}$.
D. $y = \frac{-x^2 – x + 1}{x – 1}$.
Câu 6. Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A(1; -1; 2), B(4; -3; 1)$, tọa độ của vectơ $\overrightarrow{AB}$ là
A. $(-3; 2; 1)$.
B. $(3; -2; -1)$.
C. $(5; -4; 3)$.
D. $(3; -4; -1)$.
Câu 7. Cho tứ diện $ABCD$. Phát biểu nào sau đây là sai?
A. $\overrightarrow{BA} + \overrightarrow{AB} = \vec{0}$.
B. $\overrightarrow{BA} + \overrightarrow{AC} = \overrightarrow{BC}$.
C. $\overrightarrow{AD} – \overrightarrow{AC} = \overrightarrow{CD}$.
D. $\overrightarrow{DA} + \overrightarrow{DB} = \vec{0}$.
Câu 8. Trong không gian $Oxyz$, hình chiếu vuông góc của điểm $M(3; 1; -1)$ trên trục $Oy$ có tọa độ là
A. $(3; 0; -1)$.
B. $(0; 1; 0)$.
C. $(3; 0; 0)$.
D. $(0; 0; -1)$.
Câu 9. Trong không gian $Oxyz$, cho hai vectơ $\vec{u} = (1; -4; 0)$ và $\vec{v} = (-1; -2; 1)$. Vectơ $\vec{u} + 3\vec{v}$ có tọa độ là
A. $(-2; -10; 3)$.
B. $(-2; -6; 3)$.
C. $(-4; -8; 4)$.
D. $(-2; -10; -3)$.
Câu 10. Bảng sau thống kê cân nặng của 50 quả xoài được lựa chọn ngẫu nhiên sau khi thu hoạch ở một nông trường

Khoảng biến thiên của mẫu số liệu trên là:
A. 200.
B. 700.
C. 350.
D. 40.
Câu 11. Cho mẫu số liệu ghép nhóm có phương sai bằng 32. Độ lệch chuẩn của mẫu số liệu trên là:
A. $4\sqrt{2}$.
B. 1024.
C. 16.
D. $4\sqrt{3}$.
Câu 12. Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):

Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A. $[7; 9)$.
B. $[9; 11)$.
C. $[11; 13)$.
D. $[13; 15)$.
PHẦN II. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số $y = \frac{1-x^2}{x}$.
a) Hàm số có tập xác định là $D = \mathbb{R} \setminus {0}$.
b) Đồ thị hàm số có tiệm cận đứng là đường thẳng $x = 0$.
c) $y’ = \frac{x^2-1}{x^2}$.
d) Hàm số đồng biến trên các khoảng $(-\infty; 0)$ và $(0; +\infty)$.
Câu 2. Trong không gian $Oxyz$, cho ba điểm $A(4; 2; 1)$, $B(2; -2; 3)$, $C(-1; 3; -2)$. Ta có
a) $\overrightarrow{OA} = (4; 2; 1)$.
b) $|\overrightarrow{AB}| = 3$.
c) Tọa độ trung điểm I đoạn thẳng $AB$ là $(3; 0; 2)$.
d) Tứ giác $ABCD$ là hình bình hành thì $D(1; 4; -4)$.
Câu 3. Cho hình lập phương $ABCD.A’B’C’D’$ có cạnh bằng $a$. Trên các cạnh $AA’$, $CC’$ lần lượt lấy các điểm $M$, $N$ sao cho $AM = \frac{2}{3}AA’$, $CN = NC’$.
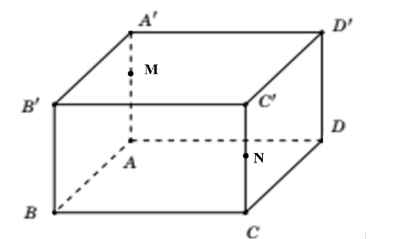
a) $\overrightarrow{AC} + \overrightarrow{DD’} = \overrightarrow{AC’}$.
b) Độ dài của vectơ $\overrightarrow{BA’} – \overrightarrow{BC’}$ bằng $2a$.
c) Góc giữa hai vectơ $\overrightarrow{AC’}$ và $\overrightarrow{DC’}$ bằng $60°$.
d) $\overrightarrow{AN} \cdot \overrightarrow{AC’} = 2a^2$.
Câu 4. Cho hàm số $y = f(x)$ có đạo hàm trên $\mathbb{R}$ và hàm số $y = f'(x)$ là hàm số bậc ba có đồ thị là đường cong như hình vẽ.
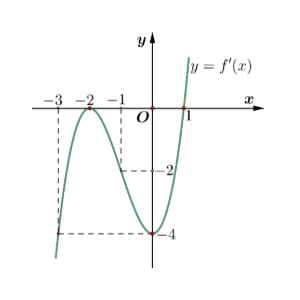
a) Hàm số $y = f(x)$ đồng biến trên khoảng $(-\infty; -2)$.
b) $f(-1) < f(0)$.
c) $\min f(x) = f(1)$.
d) Hàm số $g(x) = f(x^3 – 3)$ đồng biến trên khoảng $(-2; 0)$.
Phần III. Câu hỏi trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Giá trị nhỏ nhất của hàm số $f(x) = x^3 – 6x$ trên $[-1; 4]$ bằng bao nhiều (kết quả làm tròn đến hàng phần trăm)?
Câu 2. Trong không gian $Oxyz$, cho ba điểm $A(0; 1; 3)$, $B(3; 2; 8)$ và $C(-2; m; 4)$. Giá trị $m$ bằng bao nhiều để tam giác $ABC$ vuông tại $A$.
Câu 3. Một nhà phân tích thị trường làm việc cho một công ty sản xuất thiết bị gia dụng nhận thấy rằng nếu công ty sản xuất và bán $x$ chiếc máy xay sinh tố hàng tháng thì lợi nhuận thu được (nghìn đồng) là $P(x) = -0,3x^3 + 36x^2 + 1800x – 48000$. Lợi nhuận lớn nhất mà công ty có thể thu được khi sản xuất đúng bao nhiều chiếc máy xay sinh tố mỗi tháng.
Câu 4. Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A(4; 2; 1)$ và $B(-2; -1; 4)$. Điểm $M(a; b; c)$ thuộc đoạn thẳng AB sao cho AM=2MB. Giá trị $a + b + c$ bằng bao nhiều?
Câu 5. Ông An sử dụng hết 5 m² kính để làm bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiều (kết quả làm tròn đến hàng phần trăm)?
Câu 6. Biểu đồ dưới đây biểu diễn số lượt khách hàng đặt bàn qua hình thức trực tuyến mỗi ngày trong quý III năm 2022 của một nhà hàng. Cột thứ nhất biểu diễn số ngày có từ 1 đến dưới 6 lượt đặt bàn; cột thứ hai biểu diễn số ngày có từ 6 đến dưới 11 lượt đặt bàn; …
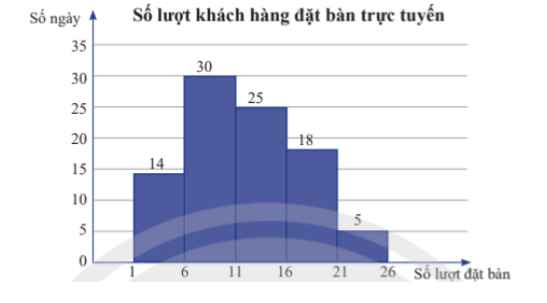
Khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi biểu đồ trên bằng bao nhiều? (kết quả làm tròn đến hàng phần trăm).

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh

