Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
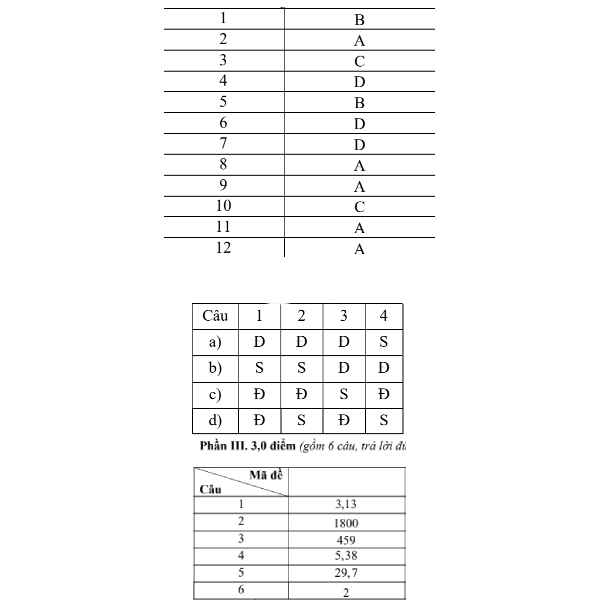
Câu 1: Cho $y = f(x)$ là hàm số bậc ba có đồ thị như hình vẽ sau:
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
A. $(-\infty; 0)$.
B. $(0; 1)$.
C. $(1; 3)$.
D. $(3; 5)$.
Câu 2: Hàm số $y = x^4 + 8x^2$ đồng biến trên khoảng nào sau đây?
A. $(0; +\infty)$.
B. $(-\infty; -2)$.
C. $(-2; 0)$.
D. $(-\infty; +\infty)$.
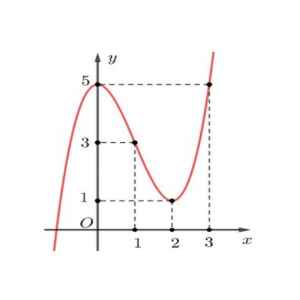
Câu 3: Cho hàm số $y = f(x)$ có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng
A. 3.
B. 1.
C. -3.
D. 2.
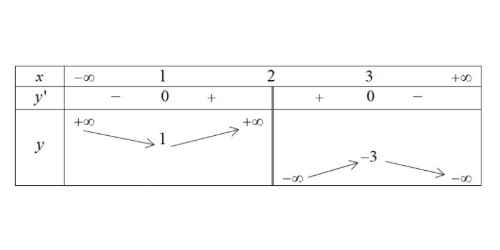
Câu 4: Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây?
A. $y = x^3 – 3x^2$.
B. $y = x^3 – 3x$.
C. $y = -x^3 + 3x^2$.
D. $y = -x^3 + 3x$.
Câu 5: Xét hình hộp tùy ý $ABCD.A’B’C’D’$ (tham khảo hình vẽ bên).
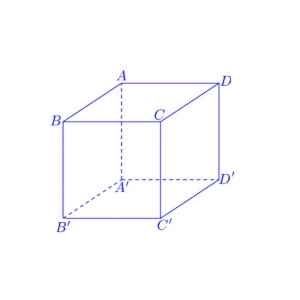
Khẳng định nào sau đây đúng?
A. $\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA’} = \overrightarrow{AB’}$.
B. $\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA’} = \overrightarrow{AC’}$.
C. $\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA’} = \overrightarrow{AD’}$.
D. $\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA’} = \overrightarrow{BD’}$.
Câu 6: Cho tứ diện đều $ABCD$ có độ dài mỗi cạnh bằng 2. Giá trị của $\overrightarrow{DA}.\overrightarrow{DB}$ bằng
A. $2\sqrt{3}$.
B. $-2\sqrt{3}$.
C. -2.
D. 2.
Câu 7: Giá trị nhỏ nhất của hàm số $y = x^4 – 2x^2 – 1$ trên đoạn $[0; 2]$ bằng
A. 7.
B. 1.
C. -1.
D. -2.
Câu 8: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y = \frac{2}{x^2 – x}$ là
A. 3.
B. 2.
C. 1.
D. 0.
Câu 9: Trong không gian với hệ trục tọa độ $Oxyz$, cho tam giác $ABC$ có $A(1; 0; 2)$, $B(2; 1; 4)$ và trọng tâm là $G(-1; 2; 0)$. Tìm tọa độ của đỉnh $C$.
A. $C(-6; 5; -6)$.
B. $C\left(\frac{2}{3}; 1; 2\right)$.
C. $C(6; -5; 6)$.
D. $C(2; 3; 6)$.
Câu 10: Trong không gian với hệ trục tọa độ $Oxyz$, cho hai vectơ $\vec{u}(-1; 1; 3)$ và $\vec{v}(1; -1; 0)$. Giá trị của $\vec{u}.\vec{v}$ bằng
A. 1.
B. 2.
C. -2.
D. -1.
Câu 11: Cho hàm số $y = \frac{ax + b}{x + c}$ ($a, b, c$ là các hằng số thực) có đồ thị như hình vẽ bên. Hai đường tiệm cận của đồ thị hàm số cắt nhau tại $I$. Tọa độ của điểm $I$ là
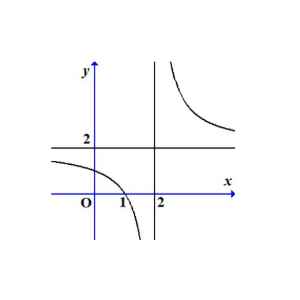
A. $(2; 2)$.
B. $(1; 2)$.
C. $(2; 1)$.
D. $(0; 0)$.
Câu 12: Điều tra cân nặng các học sinh (tính theo đơn vị kilogram) ở một lớp 12 của một trường học người ta thu được mẫu số liệu như sau:

Phương sai của mẫu số liệu trên bằng
A. 110.
B. 113.
C. 112.
D. 111.
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4.
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1: Xét hàm số $f(x) = \frac{x^2 + x}{x – 1}$ với $x \in \mathbb{R} \setminus {1}$, có đồ thị là $(H)$.
a) Đạo hàm của hàm số đó là $f'(x) = \frac{x^2 – 2x – 1}{(x – 1)^2}$ với $x \in \mathbb{R} \setminus {1}$.
b) Đường tiệm cận xiên của $(H)$ có phương trình là $y = x – 1$.
c) Khoảng cách giữa hai điểm cực trị của $(H)$ bằng $2\sqrt{10}$.
d) Giá trị nhỏ nhất của $f(x)$ trên khoảng $(1; +\infty)$ là $3 + 2\sqrt{2}$.
Câu 2: Số giờ sử dụng smartphone trong 1 ngày nghỉ của học sinh lớp 12A7 được thống kê trong bảng sau:

a) Khoảng biến thiên của mẫu số liệu trên bằng 6.
b) Giá trị trung bình của mẫu số liệu trên bằng $\frac{226}{45}$.
c) Số trung vị của mẫu số liệu trên bằng $\frac{19}{8}$.
d) Độ lệch chuẩn của mẫu số liệu trên bằng $\frac{2\sqrt{730}}{45}$.
Câu 3: Trong không gian với hệ trục tọa độ $Oxyz$, cho hình bình hành $ABCD$ có $A(-1; 3; 0)$; $B(1; 2; -1)$; $C(1; 1; -2)$.
a) $\overrightarrow{AB} = (2; -1; -1)$.
b) $\cos(\overrightarrow{AB}, \overrightarrow{AC}) = \frac{2\sqrt{2}}{3}$.
c) Diện tích của tam giác $ABC$ bằng $2\sqrt{2}$.
d) Tọa độ của điểm $D$ là $(-1; 2; -1)$.
Câu 4: Một chất điểm $M$ chuyển động trên một đường thẳng đi qua $O$. Để khảo sát chuyển động của $M$ người ta gắn trên đường thẳng đó một trục tọa độ là $Ox$ với $O$ là điểm gốc, mỗi đơn vị trên trục tương ứng với độ dài 1 mét. Xét trong 12 giây đầu tiên, tọa độ $x(t)$ của $M$ tại thời điểm $t$ giây kể từ lúc bắt đầu khảo sát được cho bởi công thức $x(t) = -\frac{t^3}{3} + 6t^2 + 4$.
a) Ban đầu $M$ ở vị trí cách $O$ một khoảng cách bằng 6 mét.
b) Vận tốc tức thời của $M$ tại thời điểm $t$ giây $(0 \leq t \leq 12)$ là $v(t) = -t^2 + 12t$ (mét/giây).
c) Trong suốt 6 giây đầu tiên, vận tốc tức thời của $M$ luôn tăng.
d) Xét trong 12 giây đầu tiên, tính từ lúc bắt đầu khảo sát đến lúc $M$ có vận tốc tức thời lớn nhất thì $M$ đi được một quãng đường dài 148 mét.
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Cho hàm số bậc ba $y = ax^3 + bx^2 + c$ có đồ thị $(C)$. Biết $(C)$ đi qua điểm $A(-2; 2)$ và nhận điểm $B(2; 3)$ làm điểm cực trị. Giá trị của $T = a + b + c$ bằng bao nhiều? (làm tròn kết quả đến hàng phần trăm).
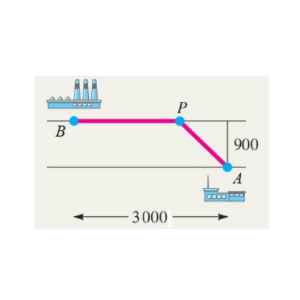
Câu 2: Một đường cáp điện được kéo từ một trạm điện $A$ ở một bên sông rộng 900 mét đến một nhà máy $B$ ở bờ bên kia của sông, nhà máy cách trạm điện 3000 mét tính xuôi theo bờ sông. Đường cáp này được mô hình hóa thành đường gấp khúc $APB$ như hình vẽ, trong đó đoạn $PB$ đặt trên bờ sống. Giá định rằng tỉ lệ giữa chi phí để kéo 1 mét cáp dưới nước và chi phí kéo 1 mét cáp trên bờ bằng 1,25. Hỏi để tiết kiệm chi phí nhất thì vị trí $P$ cách nhà máy $B$ bao nhiều mét?
Câu 3: Một người quản lý ở một trang trại nuôi cá xác định rằng: Sau $t$ tháng kể từ khi thả 300 con cá X (với $0 \leq t \leq 10$) thì khối lượng trung bình $m(t)$ tính theo kilogram của một con cá X ước tính là $m(t) = 0,45\left(0,2 + \frac{141}{155}t – 0,05t^2\right)$. Người này cũng nhận định $t$ lệ giữa số lượng cá X còn sống trong ao so với số lượng cá X thả ban đầu sau $t$ tháng kể từ ngày thả là $p(t) = \frac{31}{31 + t}$. Biết rằng sản lượng cá X tại một thời điểm được tính bằng tổng khối lượng của các con cá X đã thả còn sống trong ao lúc đó. Hỏi với những nhận định trên của người quản lý thì dự kiến trong tối đa 10 tháng nuôi, sản lượng cá X lớn nhất có thể đạt được là bao nhiều (kết quả tính theo đơn vị kilogram)?
Câu 4: Tìm hiểu về thu nhập trung bình mỗi tháng của mỗi nhân viên trong số 35 nhân viên ở một công ty, người ta thu được bảng số liệu sau:

Khoảng tứ phân vị của mẫu số liệu trên bằng bao nhiều? (làm tròn kết quả đến hàng phần trăm).
Câu 5: Tại một vị trí cụ thể ở núi Bà Đen người ta đặt có định một hệ trục tọa độ $Oxyz$, mỗi đơn vị trên mỗi trục có độ dài bằng 1 mét. Một người đứng có định tại vị trí $B(2; 0; -1)$, quan sát một chiếc cabin cáp treo và thấy rằng cabin này xuất phát từ điểm $A(-1; 4; 3)$, chuyển động thẳng đều theo hướng của vectơ $\vec{u}(1; 2; -2)$ với vận tốc 6 mét/giây. Hỏi sau 5 giây kể từ lúc xuất phát, khoảng cách giữa cabin và người quan sát bằng bao nhiều mét? (làm tròn kết quả đến hàng phần chục).
Câu 6: Trong không gian với hệ trục tọa độ $Oxyz$, cho tứ diện $ABCD$ có $A(1; 3; -2)$; $B(-1; -1; 0)$; $C(3; 1; -1)$; $D(0; 2; -2)$. Xét điểm $M$ thay đổi trên mặt phẳng $(Oxy)$. Khi $f = |\overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC}| + 3|\overrightarrow{MD}|$ đạt giá trị nhỏ nhất thì điểm $M$ có tọa độ là $(a; b; c)$. Giá trị của biểu thức $T = a + b – c$ bằng bao nhiều?

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh