PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chọn một phương án.

Câu 1. Cho hàm số có bảng biến thiên như sau:

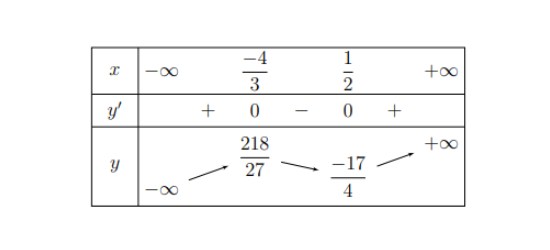
Khẳng định nào sau đây là đúng?

A. Hàm số nghịch biến trên khoảng $\left(-\infty; -\frac{4}{3}\right)$.

B. Hàm số đồng biến trên khoảng $\left(-\frac{4}{3}; \frac{1}{2}\right)$.

C. Hàm số nghịch biến trên khoảng $\left(\frac{7}{2}; +\infty\right)$.

D. Hàm số đồng biến trên khoảng $\left(-\infty; -\frac{7}{3}\right)$.

Câu 2. Giá trị lớn nhất của hàm số $y = \sqrt{x + 2} – x$ là:

A. $-\frac{5}{4}$.

B. $\sqrt{3} – 1$.

C. $\frac{9}{4}$.

D. 2.

Câu 3. Cho hàm số $y = \frac{x – 1}{x^2 – 3x + 2}$. Xét các mệnh đề sau:

(i) Đồ thị hàm số có tiệm cận ngang $y = 0$.

(ii) Đồ thị hàm số có hai tiệm cận đứng $x = 1$ và $x = 2$.

(iii) Đồ thị hàm số không có tiệm cận xiên.

Số mệnh đề đúng là:

A. 0.

B. 1.

C. 2.

D. 3.

Câu 4. Đồ thị trong hình là của hàm số $y = \frac{ax+b}{x+c}$ ($a, b, c \in \mathbb{R}$).

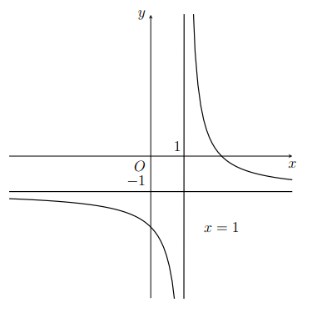
Mệnh đề nào sau đây sai.

A. Hàm số đồng biến trên các khoảng xác định.

B. Hàm số có tiệm cận đứng là $x = 1$.

C. $a + b + c = 0$.

D. Hàm số có tiệm cận ngang là $y = -1$.

Câu 5. Gọi $G$ là trọng tâm của tứ diện $ABCD$. Trong các khẳng định sau, khẳng định nào sai?

A. $\overrightarrow{AG} = \frac{1}{4}(\overrightarrow{AB} + \overrightarrow{AC} + \overrightarrow{AD})$.

B. $\overrightarrow{AG} = \frac{2}{3}(\overrightarrow{AB} + \overrightarrow{AC} + \overrightarrow{AD})$.

C. $\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} + \overrightarrow{GD} = \vec{0}$.

D. $\overrightarrow{OG} = \frac{1}{4}(\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD})$.

Câu 6. Trong không gian $Oxyz$, cho điểm $M(1; -2; 3)$. Chọn khẳng định đúng trong các khẳng định sau:

A. $\overrightarrow{OM} = \vec{i} – 2\vec{j} + 3\vec{k}$.

B. $\overrightarrow{OM} = \vec{i} + 2\vec{j} + 3\vec{k}$.

C. $\overrightarrow{OM} = \vec{i} – 2\vec{j} – 3\vec{k}$.

D. $\overrightarrow{OM} = -\vec{i} – 2\vec{j} + 3\vec{k}$.

Câu 7. Cho hình lập phương $ABCD.A’B’C’D’$. Có thể lập một hệ tọa độ $Oxyz$ có gốc $O$ trùng với đỉnh $C$ với $B, D, C’$ lần lượt thuộc trục $Ox, Oy, Oz$. Giả sử $A'(3; 2; 4)$. Tìm tọa độ điểm $B’$.

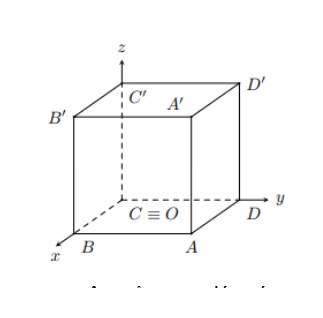
A. $B'(3; -2; 4)$.

B. $B'(3; 2; 0)$.

C. $B'(0; 2; 4)$.

D. $B'(3; 0; 4)$.

Câu 8. Cho tam giác $ABC$ biết $A(2; -1; 3)$ và trọng tâm của tam giác có tọa độ là $G(2; 1; 0)$. Khi đó $\overrightarrow{AB} + \overrightarrow{AC}$ có tọa độ là:

A. $(0; -9; 9)$.

B. $(0; 6; 9)$.

C. $(0; 9; -9)$.

D. $(0; 6; -9)$.

Câu 9. Bảng sau thống kê lại cân nặng của 50 quả dưa hấu được lựa chọn ngẫu nhiên sau khi thu hoạch ở nông trường:

Khoảng tứ phân vị của mẫu số liệu trên là:

A. 0, 15.

B. 0, 3.

C. 0, 25.

D. 0, 4.

Câu 10. Phát biểu nào sau đây không đúng về khoảng biến thiên của mẫu số liệu ghép nhóm?

A. Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số của đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên chứa dữ liệu.

B. Khoảng biến thiên của mẫu số liệu ghép nhóm luôn lớn hơn hoặc bằng khoảng biến thiên của mẫu số liệu gốc.

C. Khoảng biến thiên của mẫu số liệu ghép nhóm có thể được dùng để tìm ra các giá trị ngoại lệ của mẫu số liệu đó.

D. Khoảng biến thiên của mẫu số liệu ghép nhóm có thể được dùng để đo mức độ phân tán của mẫu số liệu.

Câu 11. Độ lệch chuẩn có ý nghĩa gì trong phân tích dữ liệu?

A. Độ lệch chuẩn chỉ ra số lượng quan sát trong mẫu dữ liệu.

B. Độ lệch chuẩn cho biết trung bình của các giá trị dữ liệu.

C. Độ lệch chuẩn đo lường mức độ biến động hoặc phân tán của các giá trị dữ liệu so với giá trị trung bình.

D. Độ lệch chuẩn cho biết tổng các giá trị dữ liệu.

Câu 12. Ở cuộc thi nhảy cao của học sinh 12. Kết quả được thống kê như sau:

Giá trị phương sai về độ cao bằng:

A. 26,14.

B. 26,41.

C. 18,04.

D. 26,9.

PHẦN II. Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1. Cho hàm số $y = f(x) = \frac{x + 3x}{x – 1}$.

a) Hàm số $f(x)$ đồng biến trên khoảng $(-\infty; 1)$.

b) Giá trị cực đại của hàm số $f(x)$ là 1.

c) Hàm số $f(x)$ có ba điểm cực trị.

d) Đồ thị hàm số có tiệm cận xiên tạo với hai trục tọa độ một tam giác có diện tích bằng 8.

Câu 2. Cho tứ diện $ABCD$ có $AB \perp (BCD)$, $AB = 4cm$, tam giác $BCD$ đều cạnh 3 cm, $G$ là trọng tâm tam giác $BCD$, điểm $M$ là trung điểm $CD$. Đặt $\overrightarrow{AB} = \vec{a}$, $\overrightarrow{AC} = \vec{b}$, $\overrightarrow{AD} = \vec{c}$.

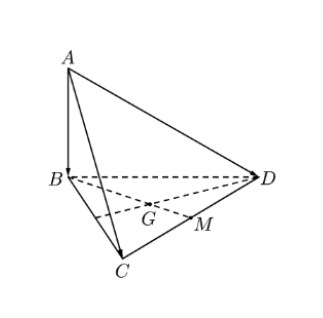
a) $\overrightarrow{AB}.\overrightarrow{MC} = 0$.

b) $|\overrightarrow{AD} + 2\overrightarrow{MC}| = 5$ cm.

c) $\cos \cos(\overrightarrow{AB}, \overrightarrow{AM}) = \frac{4\sqrt{91}}{91}$.

d) $\overrightarrow{AG} = \frac{1}{3}(\vec{a} + \vec{b} + \vec{c})$.

Câu 3. Cho hình hộp $ABCD.A’B’C’D’$, biết điểm $A(0; 0; 0)$, $B(1; 0; 0)$, $C(1; 2; 0)$, $D'(-1; 3; 5)$. Gọi $M, N$ lần lượt là tâm của các hình bình hành $ABBA’$, $ADD’A’$.

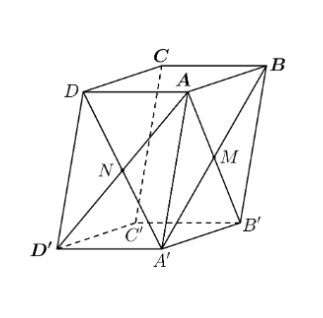
a) Tọa độ $D(0; 2; 0)$.

b) Tọa độ $A'(-1; 1; 5)$.

c) Tọa độ $\overrightarrow{MN} = (-1; 2; 0)$.

d) $|\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{CC’}| = \sqrt{29}$.

Câu 4. Biểu đồ tần suất hình quạt trong hình bên mô tả bảng phân bố tần suất ghép nhóm của dữ liệu điểm thi của 40 học sinh lớp 12A trong kì thi học kì 1 môn Toán (thang điểm 10).

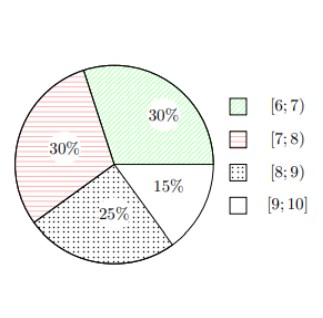
a) Tần số của các giá trị đại diện 6,5; 7,5; 8,5; 9,5 của các nhóm lần lượt là 12; 12; 9; 7.

b) Điểm thi trung bình môn Toán của lớp 12A là 7,75.

c) Khoảng tứ phân vị của bảng số liệu là $\Delta_Q = \frac{5}{3}$.

d) Độ lệch chuẩn của mẫu số liệu là 7,82.

PHẦN III. Câu trắc nghiệm trả lời ngắn.

Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1. Mảng trượt của một cầu trượt cho trẻ em (Hình a) được uốn từ một tấm kim loại có bề rộng 80 cm, mặt cắt được mô tả ở Hình b. Nhà thiết kế khuyến cáo, diện tích mặt cắt càng lớn thì càng đảm bảo an toàn cho trẻ em.

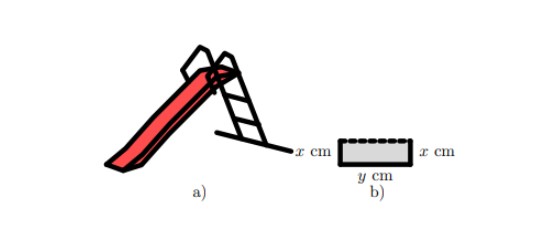
Với $x$ đạt giá trị bằng bao nhiều thì cầu trượt đảm bảo an toàn nhất cho trẻ em?

Câu 2. Trong không gian $Oxyz$, cho hình lăng trụ tam giác $ABC.A’B’C’$ có $A(1; 0; 2)$, $B(3; 2; 5)$, $C(11; -3; 8)$. Điểm $D(a; b; c)$ sao cho $ABCD.A’B’C’D’$ là hình hộp. Tính $a + b + c$.

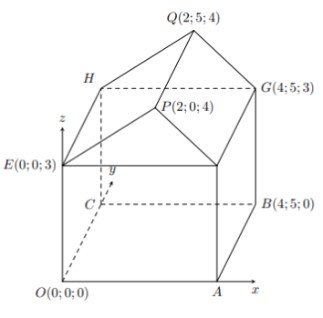
Câu 3. Hình minh họa so đồ một ngôi nhà trong hệ trục tọa độ $Oxyz$, trong đó nền nhà, bốn bức tường và hai mái nhà đều là hình chữ nhật. Tính góc độc của mái nhà, tức là tìm số đo của góc nhị diện có cạnh là đường thẳng $FG$, hai mặt lần lượt là $(FGQP)$ và $(FGHE)$ (làm tròn kết quả đến hàng phần mười của độ).

Câu 4. Thu nhập của các cặp vợ chồng trong một năm ở một khu phố được thể hiện qua biểu đồ cột sau:

Tính khoảng tứ phân vị của mẫu thu nhập trên (làm tròn đến hàng đơn vị).

Câu 5. Bạn Minh Nhân sử dụng điện thoại thông minh để chơi game trong một ngày. Số lần bạn sử dụng điện thoại được thống kê như sau:

Hãy tính tỉ số phần trăm (làm tròn 1 chữ số thập phân) giữa độ lệch chuẩn và giá trị trung bình.

Câu 6. Cho hàm số $y = \frac{2x^2 – x + 7}{x – 1}$ có đồ thị $(C)$. Biết rằng $(C)$ có hai điểm cực trị, tính khoảng cách từ điểm $O$ đến đường thẳng đi qua hai điểm cực trị đó.

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh