PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1. Giá trị lớn nhất của hàm số $y = -x^3 + 3x + 1$ trên khoảng $(0; +\infty)$ bằng:

A. 1.

B. -1.

C. 5.

D. 3.

Câu 2. Trong không gian $Oxyz$, cho $A(1; 0; 1)$. Tìm tọa độ điểm $C$ thỏa mãn $\overrightarrow{AC} = (0; 6; 1)$.

A. $C(-1; -6; -2)$.

B. $C(-1; 6; -1)$.

C. $C(1; 6; 0)$.

D. $C(1; 6; 2)$.

Câu 3. Cho hình hộp $ABCD.A’B’C’D’$. Gọi $I, J$ lần lượt là trung điểm của $AB’$ và $CD’$. Khẳng định nào dưới đây là đúng?

A. $\overrightarrow{AI} = \overrightarrow{CJ}$.

B. $\overrightarrow{D’A} = \overrightarrow{IJ}$.

C. $\overrightarrow{BI} = \overrightarrow{D’J}$.

D. $\overrightarrow{AI} = \overrightarrow{JC}$.

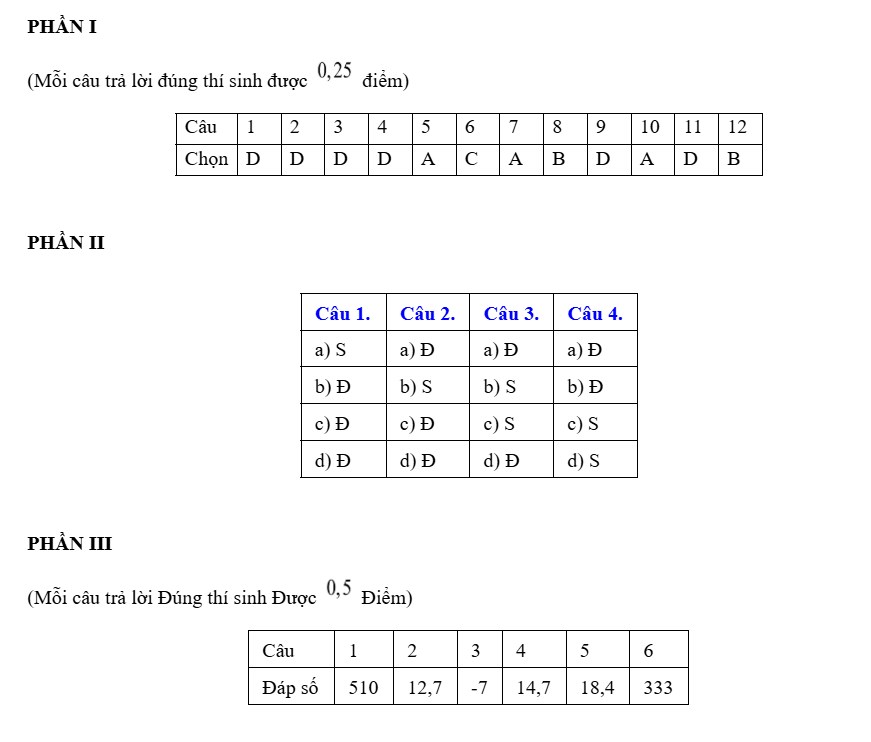
Câu 4. Đường cong trong hình vẽ bên là đồ thị của hàm số có dạng $y = ax^3 + bx^2 + cx + d$ ($a \neq 0$). Hàm số đồng biến trên khoảng nào dưới đây?

A. $(-\infty; 1)$.

B. $(-1; +\infty)$.

C. $(1; +\infty)$.

D. $(-1; 1)$.

Câu 5. Cho lăng trụ tam giác $ABC.A’B’C’$ có $\overrightarrow{AA’} = \vec{a}$, $\overrightarrow{AB} = \vec{b}$, $\overrightarrow{AC} = \vec{c}$. Hãy phân tích (biểu diễn) vectơ $\overrightarrow{BC’}$ qua các vectơ $\vec{a}, \vec{b}, \vec{c}$

A. $\overrightarrow{BC’} = \vec{a} – \vec{b} + \vec{c}$.

B. $\overrightarrow{BC’} = -\vec{a} + \vec{b} – \vec{c}$.

C. $\overrightarrow{BC’} = -\vec{a} – \vec{b} + \vec{c}$.

D. $\overrightarrow{BC’} = \vec{a} + \vec{b} – \vec{c}$.

Câu 6. Cho hàm số $y = f(x)$ có $\lim_{x \to -\infty} f(x) = -\infty$ và $\lim_{x \to +\infty} f(x) = 2$. Mệnh đề nào sau đây đúng?

A. Đường thẳng $x = 3$ không phải là tiệm cận của đồ thị hàm số $y = f(x)$.

B. Đường thẳng $y = 2$ là tiệm cận ngang của đồ thị hàm số $y = f(x)$.

C. Đường thẳng $x = 3$ là tiệm cận đứng của đồ thị hàm số $y = f(x)$.

D. Đồ thị hàm số $y = f(x)$ không có tiệm cận đứng.

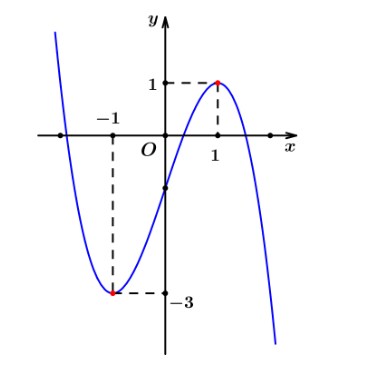
Câu 7. Cho đường cong $(C): y = ax^3 + bx^2 + cx + d$ có đồ thị như hình bên.

Khẳng định nào sau đây là đúng?

A. $a > 0, b > 0, c < 0, d < 0$.

B. $a > 0, b < 0, c < 0, d < 0$.

C. $a > 0, b > 0, c > 0, d > 0$.

D. $a < 0, b > 0, c > 0, d < 0$.

Câu 8. Trong không gian $Oxyz$, cho ba điểm $A(-1; 0; 2)$, $B(2; 1; -3)$ và $C(1; -1; 0)$. Tìm tọa độ điểm $D$ sao cho $ABCD$ là hình bình hành.

A. $D(0; 2; -1)$.

B. $D(-2; -2; 5)$.

C. $D(2; 2; -5)$.

D. $D(-2; 2; 5)$.

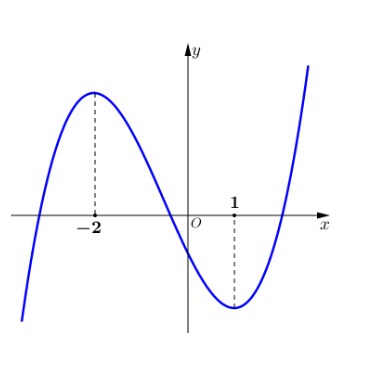
Câu 9. Biểu đồ sau biểu diễn tốc độ tăng trường GDP của Nhật Bản trong giai đoạn 1990 đến 2005. Hãy tìm khoảng biến thiên của mẫu số liệu đó.

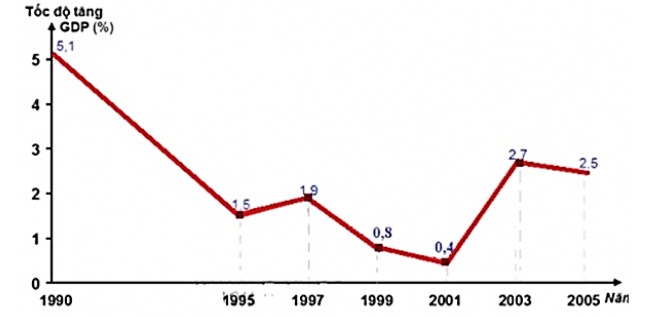
A. 5,1.

B. 5,5.

C. 0,4.

D. 4,7.

Câu 10. Nhiệt độ trung bình hàng tháng trong một năm được ghi lại trong bảng sau:

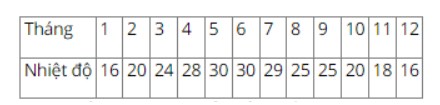
Tìm khoảng tứ phân vị của bảng số liệu trên.

A. 9,5.

B. 28,5.

C. 24,5.

D. 19.

Câu 11. Sản lượng lúa (đơn vị ha) của 40 thửa ruộng có cùng diện tích được trình bày trên bảng số liệu sau:

Tính phương sai của bảng số liệu trên.

A. 1,74.

B. 1,73.

C. 1,75.

D. 1,76.

Câu 12: Theo kết quả thống kê điểm thi giữa kỳ 2 môn toán khối 11 của một trường THPT, người ta tính được phương sai của bảng thống kê đó là $s_x^2 = 0,573$. Độ lệch chuẩn của bảng thống kê đó bằng

A. 0,812.

B. 0,757.

C. 0,936.

D. 0,657.

PHẦN II. Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1. Cho hàm số $y = \frac{2x – m}{x – 1}$. Xét tính đúng sai của các mệnh đề

a) Hàm số đồng biến trên khoảng xác định của nó khi $m > 2$.

b) Khi $m = -1$ thì $y’ = \frac{-3}{(x – 1)^2}$.

c) Khi $m = 0$ thì đồ thị hàm số cắt trục $Ox$ tại điểm $x = 1$.

d) Tập xác định của hàm số là $D = \mathbb{R} \setminus {1}$.

Câu 2. Cho hàm số $y = \frac{-x^2 – 3x + 4}{x – 3}$ có đồ thị là $(C)$.

a) Đồ thị $(C)$ có hai điểm cực trị nằm 2 phía đối với $Oy$.

b) Đồ thị không cắt trục $Ox$.

c) Đồ thị $(C)$ có tiệm cận xiên là $y = -x – 6$.

d) Đồ thị $(C)$ nhận giao điểm $I(3; -9)$ làm tâm đối xứng.

Câu 3. Hình minh họa so đồ một ngôi nhà trong hệ trục tọa độ $Oxyz$, trong đó nền nhà, bốn bức tường và hai mái nhà đều là hình chữ nhật.

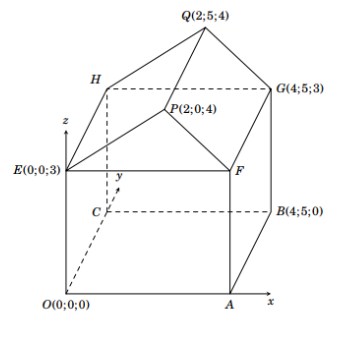
a) Góc nhị diện có cạnh là đường thẳng $FG$, hai mặt lần lượt là $(FGQP)$ và $(FGHE)$ gọi là góc độc của mái nhà. Số đo của góc độc của mái nhà bằng $26,6°$ (làm tròn kết quả đến hàng phần mười của độ).

b) Chiều cao của ngôi nhà là 4.

c) Tọa độ của các điểm $A(5; 0; 0)$.

d) Tọa độ của các điểm $H(0; 5; 3)$.

Câu 4. Cho mẫu số liệu về số giờ xem ti vi trong một ngày của một số người như sau:

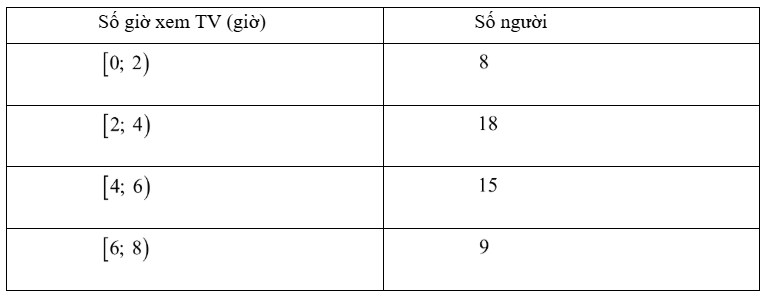
a) Có 9 người xem TV từ 6 đến 8 giờ mỗi ngày.

b) Khoảng biến thiên của mẫu số liệu là 8 giờ.

c) Giá trị trung bình có thể ước tính là khoảng 3 giờ xem TV mỗi ngày.

d) Phương sai của mẫu số liệu này có thể ước tính là 2 giờ.

PHẦN III. Câu trắc nghiệm trả lời ngắn.

Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1. Một thiết bị thăm dò đáy biển như hình vẽ được đẩy bởi một lực $\vec{f} = (5; 4; -2)$ (đơn vị: N) giúp thiết bị thực hiện độ dời $\vec{d} = (70; 20; -40)$ (đơn vị: m). Tính công sinh bởi lực $\vec{f}$.

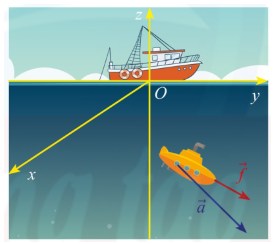
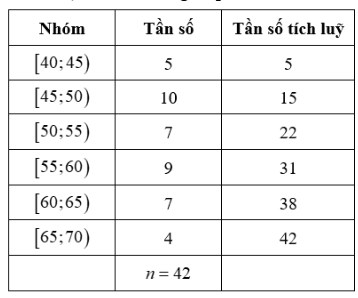
Câu 2. Bảng dưới biểu diễn mẫu số liệu ghép nhóm về chiều cao của 42 mẫu cây ở một vườn thực vật (đơn vị: centimet). Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó (làm tròn kết quả đến hàng phần mười).

Câu 3. Trong không gian $Oxyz$ cho $A(-1; 4; 2)$, $B(3; 2; 1)$, $C(-2; 0; 2)$. Gọi $D(a; b; c)$ là điểm sao cho $ABCD$ là hình thang có đáy $AD$ và diện tích hình thang $ABCD$ gấp ba lần diện tích tam giác $ABC$. Tính $a + b + c$?

Câu 4. Một cửa hàng nhận làm những chiếc xô bằng nhôm hình trụ không có nắp đủ chứa được gì x₁10 lít nước. Hỏi bán kính đáy (đơn vị cm, làm tròn đến hàng phần chục) của chiếc xô bằng bao nhiều để cửa hàng tốn ít nguyên vật liệu nhất. (Làm tròn đến hàng phần mười)

Câu 5. Để giảm nhiệt độ trong phòng từ $28^0C$, một hệ thống làm mát được phép hoạt động trong 10 phút. Gọi $T$ (đơn vị $^0C$) là nhiệt độ phòng ở phút thứ $t$ được cho bởi công thức $T = -0,008t^3 – 0,16t + 28$ với $t \in [1; 10]$. Tìm nhiệt độ thấp nhất trong phòng đạt được trong thời gian 10 phút kể từ khi hệ thống làm mát bắt đầu hoạt động. (Làm tròn đến hàng phần mười)

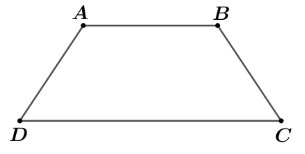
Câu 6. Một người nông dân có 3 tấm lưới thép B40, mỗi tấm dài 16m và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân ABCD như hình vẽ, (trong đó: bờ sông là đường thẳng DC không phải rào và mỗi tấm là một cạnh của hình thang). Hỏi ông ấy có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiều m²? (Làm tròn đến hàng đơn vị)

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh