PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.

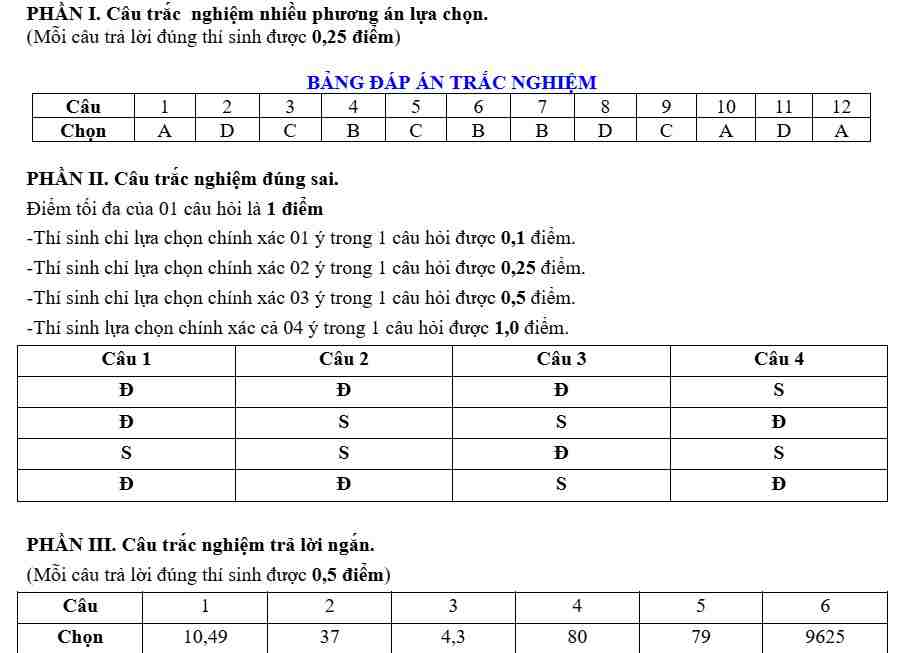
Câu 1: Cho hàm số $y = f(x)$ liên tục trên $\mathbb{R}$ và có đồ thị là đường cong trong hình dưới đây. Cực tiểu của hàm số $y = f(x)$ bằng

A. $-2$.

B. $-1$.

C. $2$.

D. $3$.

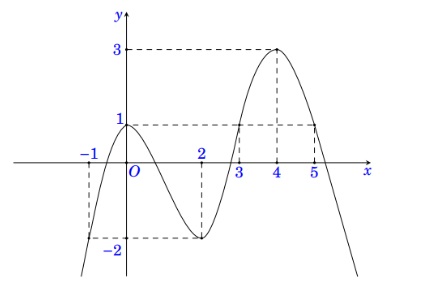
Câu 2: Cho hàm số $y = f(x)$ liên tục trên đoạn $[-1; 3]$ có bảng biến thiên như sau

Gọi $M, m$ theo thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f(x)$ trên đoạn $[-1; 3]$. Giá trị $M.m$ bằng

A. $M.m = 4$.

B. $M.m = 5$.

C. $M.m = -3$.

D. $M.m = 0$.

Câu 3: Cho hàm số $y = f(x)$ thỏa mãn $\lim_{x \to 2^+} f(x) = 1$; $\lim_{x \to 2^-} f(x) = 1$; $\lim_{x \to +\infty} f(x) = 2$ và $\lim_{x \to -\infty} f(x) = 2$. Khẳng định nào sau đây là đúng?

A. Đường thẳng $x = 2$ là tiệm cận đứng của đồ thị hàm số.

B. Đường thẳng $x = 1$ là tiệm cận ngang của đồ thị hàm số.

C. Đường thẳng $y = 2$ là tiệm cận ngang của đồ thị hàm số.

D. Đường thẳng $y = 1$ là tiệm cận ngang của đồ thị hàm số.

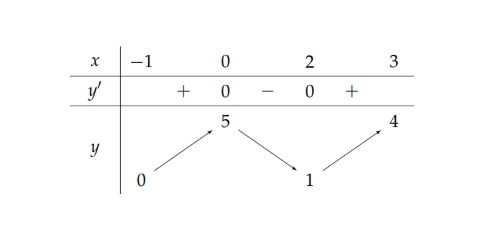
Câu 4: Cho hàm số $y = f(x)$ xác định trên $\mathbb{R} \setminus {1}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau

Bảng biến thiên trên của hàm số nào trong các hàm số sau?

A. $y = \frac{-x + 2}{x – 1}$.

B. $y = \frac{x + 2}{x – 1}$.

C. $y = \frac{x + 2}{x + 1}$.

D. $y = \frac{x – 3}{x – 1}$.

Câu 5: Cho hình lập phương $ABCD.A’B’C’D’$ cạnh $a$. Khẳng định nào sau đây sai?

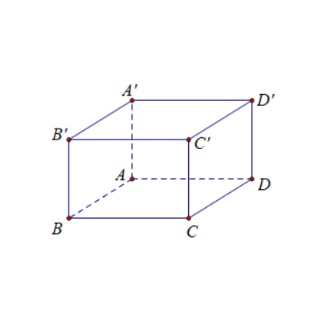
A. $|\overrightarrow{BD}| = a\sqrt{2}$.

B. $|\overrightarrow{BD’}| = a\sqrt{3}$.

C. $\overrightarrow{AC} + \overrightarrow{A’C’} = \vec{0}$.

D. $\overrightarrow{BA} + \overrightarrow{BC} + \overrightarrow{BB’} = \overrightarrow{BD’}$.

Câu 6: Trong không gian $Oxyz$, cho vector $\overrightarrow{MO} = 2\vec{j} – 3\vec{i} + \vec{k}$. Tọa độ điểm $M$ là

A. $M(2; -3; 1)$.

B. $M(3; -2; -1)$

C. $M(-3; 2; 1)$

D. $M(-2; 3; -1)$

Câu 7: Số lượng khách hàng nữ mua hàng thời trang trong một ngày của một cửa hàng được thống kê trong bảng tần số ghép nhóm như sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là

A. 20

B. 50

C. 6

D. 60

Câu 8: Khảo sát về độ ẩm không khí trung bình các tháng năm 2022 tại Đà Nẵng (đơn vị: %), người ta được một mẫu dữ liệu ghép nhóm như sau:

Phương sai của mẫu số liệu ghép nhóm trên là

A. 134,25.

B. 3,34.

C. 80,25.

D. 11,1875.

Câu 9: Cho $y = f(x)$ liên tục và đồng biến trên khoảng $(3; 11)$. Số nghiệm nguyên của bất phương trình $f(11x) > f(x^2)$ trên khoảng $(3; 11)$ là

A. 9.

B. 8.

C. 7.

D. 10.

Câu 10: Một chất điểm chuyển động theo quy luật $s(t) = 4t^2 – \frac{2t^3}{3}$ (m). Thời điểm $t$ (giây) mà tại đó tốc độ $v$ (m/s) của chuyển động đạt giá trị lớn nhất là

A. $t = 2$.

B. $t = 4$.

C. $t = 1$.

D. $t = 3$.

Câu 11: Cho hàm số $y = f(x)$ liên tục trên $\mathbb{R}$ và có đạo hàm $f'(x) = (x + 1)(x – 4)^2(x – 8)^3, \forall x \in \mathbb{R}$. Khẳng định nào sau đây đúng?

A. $f(6) < f(8)$.

B. $f(8) > f(12)$.

C. $f(-1) < f(4)$.

D. $f(-1) > f(8)$.

Câu 12: Trong không gian $Oxyz$, cho tam giác $ABC$ vuông tại C với điểm $A(1; 2; 0)$, $B(2; -1; 1)$ và điểm C có hoành độ dương trên trục $Ox$. Diện tích tam giác $ABC$ bằng

A. $\sqrt{6}$.

B. $2\sqrt{6}$.

C. $\sqrt{30}$.

D. $\frac{\sqrt{30}}{2}$.

PHẦN II. Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S).

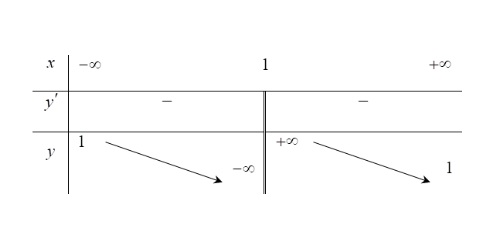
Câu 1. Cho hàm số $y = f(x) = ax^3 + bx^2 + cx + d$ có bảng biến thiên như sau

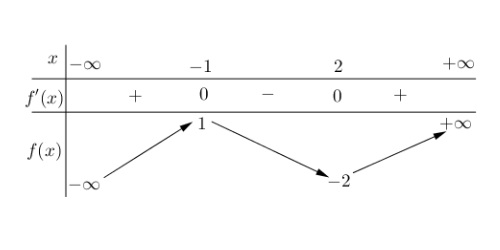
Khi đó:

a) Hàm số đạt cực tiểu tại điểm $x = 2$.

b) Hàm số nghịch biến trên khoảng $(0; 1)$.

c) Trên khoảng $(-\infty; 2)$, hàm số có giá trị lớn nhất là 1 và có giá trị nhỏ nhất là $-2$.

d) Đồ thị hàm số $y = \frac{2024}{f(x) + 1}$ có 4 đường tiệm cận.

Câu 2. Biết hàm số $y = f(x) = \frac{x + a}{x + 1}$ ($a$ là số thực cho trước và $a \neq 1$) có đồ thị như hình vẽ bên dưới.

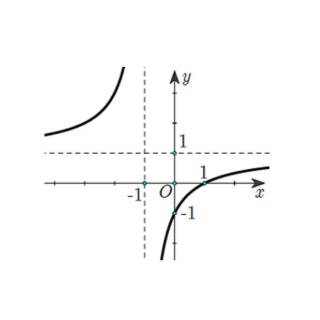
a) $f'(x) > 0, \forall x \neq -1$ và hàm số không có điểm cực trị.

b) Tâm đối xứng của đồ thị hàm số là $I(-1; 1)$.

c) $\max_{[0;3]} f(x) = \frac{1}{3}$ đạt được khi $x = 3$.

d) Số đường thẳng cắt đồ thị $f(x)$ tại những điểm tọa độ nguyên là 6.

Câu 3. Hình minh họa sơ đồ một ngôi nhà trong không gian $Oxyz$ với độ dài đơn vị trên các trục tọa độ bằng $1m$, trong đó nền nhà, bốn bức tường và hai mái nhà đều là hình chữ nhật

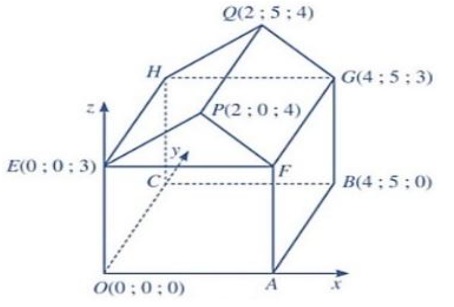
a) [NB] Tọa độ điểm $H(0; 5; 3)$.

b) [TH] Diện tích ngôi nhà là $12(m^2)$.

c) [TH] Hình chiếu vuông góc $K$ của điểm $O$ xuống nền nhà có tọa độ $K(2; 5; 0)$.

d) [VD] Thể tích phần không gian của ngôi nhà bằng $60(m^3)$.

Câu 4. Khảo sát thời gian tập thể dục trong ngày của học sinh lớp 12A và 12B khối 12 thu được mẫu số liệu ghép nhóm sau:

a) [NB] Cỡ mẫu số liệu của hai lớp là $n = 40$

b) [TH] Bảng thống kê thời gian tập thể dục theo giá trị đại diện là

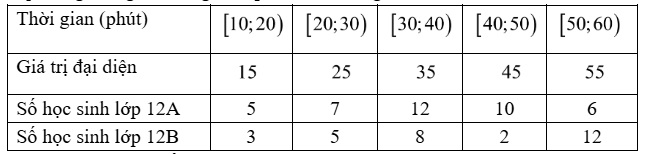
c) [TH] Thời gian tập thể dục trung bình của học sinh lớp 12A lớn hơn thời gian tập thể dục trung bình của học sinh lớp 12B.

d) [VD] Phương sai của mẫu số liệu học sinh lớp 12A là $150,9075$ và độ lệch chuẩn của mẫu số liệu học sinh lớp 12B là $14,083$.

PHẦN III. Câu trắc nghiệm trả lời ngắn.

Thí sinh trả lời từ câu 1 đến câu 6.

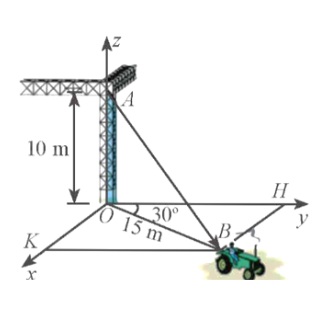
Câu 1. Một chiếc xe đang kéo căng sợi dây cáp AB trong công trường xây dựng, trên đó đã thiết lập hệ tọa độ như hình bên, với độ dài đơn vị trên các trục tọa độ bằng 1m. Tọa độ của vector $\overrightarrow{AB} = (a, b, c)$. Khi đó $a + b + c = ?$ (làm tròn đến hàng phần trăm)

Câu 2. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB = a$, $BC = 2a\sqrt{2}$, $SA = a$ và $SA$ vuông góc với đáy $ABCD$. Gọi $G$ là trọng tâm của tam giác $SBD$. Độ dài $CG$ bằng $\frac{a\sqrt{m}}{3}$. Tìm $m$.

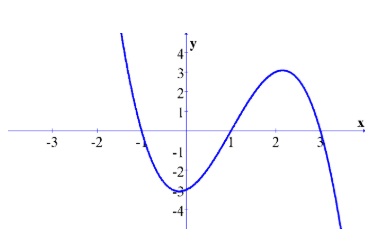
Câu 3. Cho hàm số $y = f(x)$ có đạo hàm trên $\mathbb{R}$, thỏa mãn $f(-1) = f(3) = 0$ và đồ thị của hàm số $y = f'(x)$ có dạng như hình dưới đây. Hàm số $y = (f(x))^2$ nghịch biến trên các khoảng $(-\infty; a)$ và $(b; c)$. Tính giá trị của biểu thức $P = a^2 + b^2 + \frac{c^2}{4}$ (Kết quả làm tròn đến hàng phần chục).

Câu 4. Một tấm bạt hình vuông cạnh $20m$ như hình vẽ dưới đây. Người ta dự tính cắt phần tô đậm của tấm bạt rồi gấp và may lại (các đường may không đáng kể), nhằm mục đích phủ lên tập đến trang trí (thấp đáng hình chóp tứ giác đều) để tránh lưu hai thấp khi trời mưa.

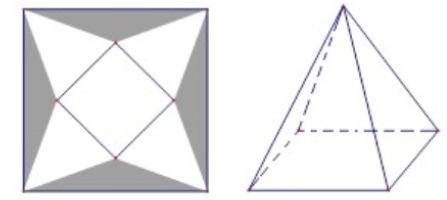
Biết khối chóp hình thành sau khi gấp và may lại cần thể tích lớn nhất thì mỗi phụ kín thấp đến. Hỏi phần diện tích tấm bạt bị cắt là bao nhiều để đảm bảo yêu cầu trên.

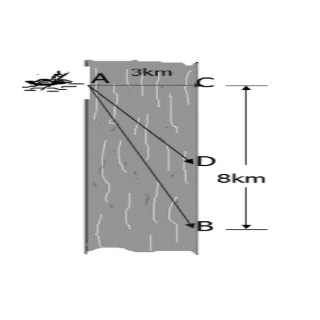
Câu 5: Một người dân ông muốn chèo thuyền ở vị trí $A$ tới điểm $B$ về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng $3km$ (như hình vẽ). Anh có thể chèo thuyền của mình trực tiếp qua sông để đến $C$ và sau đó chạy đến $B$, hay có thể chèo trực tiếp đến $B$, hoặc anh ta có thể chèo thuyền đến một điểm $D$ giữa $C$ và $B$ rồi sau đó chạy đến $B$. Biết anh ấy có thể chèo thuyền với vận tốc $5km/h$, chạy $10km/h$ và quãng đường $BC = 8km$. Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người dân ông. Gọi $t$ là thời gian ngắn nhất (làm tròn đến đơn vị: phút) để người dân ông đến $B$. Tính $t$.

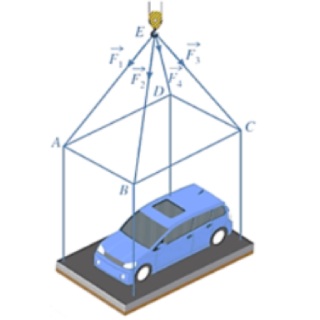
Câu 6: Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình vuông $ABCD$, mặt phẳng $(ABCD)$ song song với mặt phẳng nằm ngang. Khung sắt đó được treo vào móc $E$ của chiếc cần cẩu sao cho các đoạn dây cáp $EA, EB, EC, ED$ có độ dài bằng nhau và cùng tạo với mặt phẳng $(ABCD)$ một góc bằng $60°$ như hình vẽ. Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng và các lực căng $\vec{F_1}, \vec{F_2}, \vec{F_3}, \vec{F_4}$ đều có cường độ bằng nhau. Biết rằng nếu giảm độ dài các đoạn dây cáp $EA, EB, EC, ED$ sao cho góc hợp bởi các dây cáp đó và mặt phẳng $(ABCD)$ đều giảm $15°$ thì lực căng mỗi sợi cáp đều tăng thêm $725N$. Tính trọng lượng của chiếc xe ô tô biết trọng lượng của khung sắt là $1550N$ (kết quả làm tròn đến hàng đơn vị).

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh