Phần I. Câu trắc nghiệm nhiều phương án chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.

Câu 1. Cho hàm số $f(x)$ có bảng biến thiên như sau:

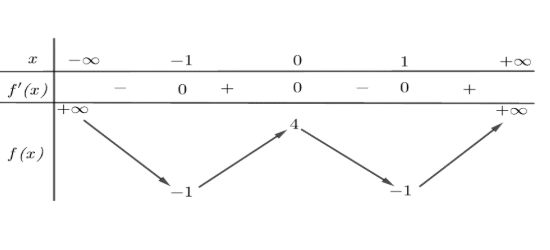
Trong khoảng $(0; +\infty)$, hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. $(-\infty; -1)$.

B. $(-1; 0)$.

C. $(0; 1)$.

D. $(1; +\infty)$.

Câu 2. Cho hàm số $f(x)$, bảng xét dấu của $f'(x)$ như sau:

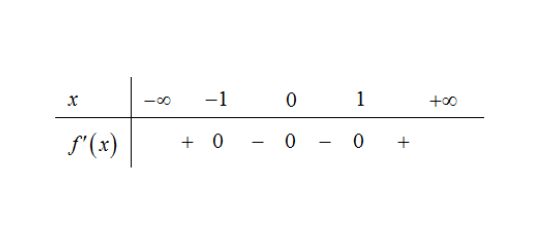
Số điểm cực trị của hàm số đã cho là

A. 0.

B. 2.

C. 1.

D. 3.

Câu 3. Giá trị nhỏ nhất của hàm số $f(x) = x^3 – 21x$ trên đoạn $[2; 19]$ bằng

A. $-36$.

B. $-14\sqrt{7}$.

C. $14\sqrt{7}$.

D. $-34$.

Câu 4. Tiệm cận ngang của đồ thị hàm số $y = \frac{x-2}{x+1}$ là

A. $y = -2$.

B. $y = 1$.

C. $x = -1$.

D. $x = 2$.

Câu 5. Đường tiệm cận xiên của đồ thị hàm số $y = \frac{2x^2 + x – 2}{x + 1}$ là

A. $y = 2$.

B. $y = 2x – 1$.

C. $y = -1$.

D. $y = 2x + 1$.

Câu 6. Bảng biến thiên sau là của hàm số nào dưới đây?

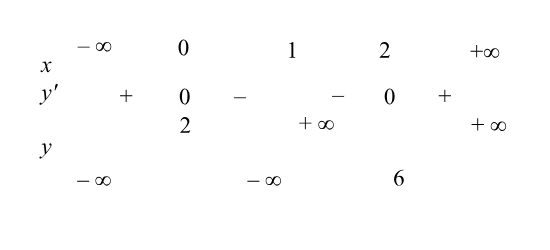
A. $y = \frac{x^2 + 4x – 2}{x – 1}$.

B. $y = \frac{x^2 + 2x – 2}{x – 1}$.

C. $y = \frac{x^2 + 2x – 2}{x + 1}$.

D. $y = \frac{x^2 + 2}{x – 1}$.

Câu 7. Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?

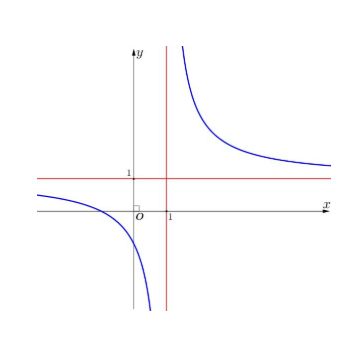
A. $y = \frac{x + 2}{x + 1}$.

B. $y = \frac{x – 1}{x + 1}$.

C. $y = \frac{-2x + 1}{x – 1}$.

D. $y = \frac{x + 1}{x – 1}$.

Câu 8. Cho tứ diện $ABCD$. Hỏi có bao nhiều vectơ khác vectơ $\vec{0}$ mà mỗi vectơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện $ABCD$?

A. 12.

B. 4.

C. 10.

D. 8.

Câu 9. Cho hình lập phương $ABCD.A’B’C’D’$. Mệnh đề nào sau đây sai?

A. $\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA’} = \overrightarrow{AC’}$.

B. $\overrightarrow{AC’} = \overrightarrow{AB} + \overrightarrow{AD}$.

C. $|\overrightarrow{AB}| = |\overrightarrow{CD}|$.

D. $\overrightarrow{AB} = \overrightarrow{CD}$.

Câu 10. Trong không gian $Oxyz$, cho điểm $A(1; 2; -3)$. Hình chiếu vuông góc của $A$ lên mặt phẳng $(Oxy)$ có tọa độ là

A. $(0; 2; -3)$.

B. $(1; 0; -3)$.

C. $(1; 2; 0)$.

D. $(1; 0; 0)$.

Câu 11. Trong không gian với hệ trục tọa độ $Oxyz$, cho $\vec{a} = (2; -3; 3)$, $\vec{b} = (0; 2; -1)$, $\vec{c} = (3; -1; 5)$. Tìm tọa độ của vectơ $\vec{u} = 2\vec{a} + 3\vec{b} – 2\vec{c}$.

A. $(10; -2; 13)$.

B. $(-2; 2; -7)$.

C. $(-2; -2; 7)$.

D. $(-2; 2; 7)$.

Câu 12. Một công ty xây dựng khảo sát khách hàng xem họ có nhu cầu mua nhà ở mức giá nào. Kết quả khảo sát được ghi lại ở bảng sau:

Khoảng biến thiên $R$ của mẫu số liệu ghép nhóm trên là.

A. $R = 4$.

B. $R = 20$.

C. $R = 9$.

D. $R = 108$.

Phần 2. Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai

Câu 1. Cho hàm số $y = \frac{x^3}{3} – 2x^2 + 3x – 1$.

a) $f'(x) = 3x^2 – 4x + 3$.

b) Hàm số nghịch biến trên khoảng $(1; 3)$.

c) Hàm số đạt cực tiểu tại điểm $x = 1$.

d) $f(1) – f(2) > 0$

Câu 2. Sử dụng đồ thị hàm số $y = f(x)$

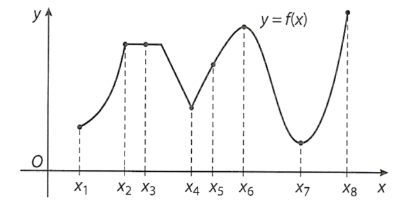
Xét tính đúng sai của các mệnh đề sau

a) Hàm số có tập xác định $D = [x_1; x_8]$.

b) Hàm số đồng biến trên khoảng $(x_1; x_4)$.

c) Hàm số có giá trị lớn nhất là $f(x_6)$.

d) Hàm số đạt cực tiểu tại các điểm $x_4$ và $x_7$.

Câu 3. Cho hàm số $f(x) = ax^3 + bx^2 + cx + d$ có đồ thị như hình vẽ.

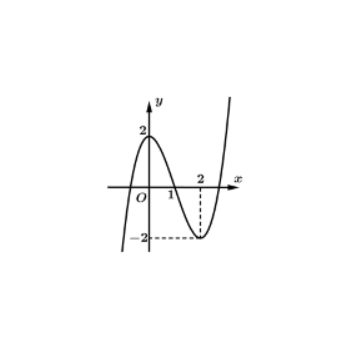
Xét tính đúng sai của các mệnh đề sau

a) $d = 1$

b) Giá trị cực đại của hàm số đã cho bằng 2.

c) Hàm số $y = f(x)$ đồng biến trên khoảng $(0; 2)$.

d) Phương trình $2f(x) + 1 = 0$ có ba nghiệm phân biệt.

Câu 4. Một tháp trung tâm kiểm soát không lưu ở sân bay cao 80 m sử dụng ra đa có phạm vi theo dõi 500km được đặt trên đỉnh tháp. Chọn hệ trục tọa độ $Oxyz$ có gốc $O$ trùng với vị trí chân tháp, mặt phẳng $(Oxy)$ trùng với mặt đất sao cho trục $Ox$ hướng về phía tây, trục $Oy$ hướng về phía nam, trục $Oz$ hướng thẳng đứng lên phía trên (Hình) (đơn vị trên mỗi trục tính theo kilômét).

Một máy bay tại vị trí $A$ cách mặt đất 10km, cách 300km về phía đông và 200km về phía bắc so với tháp trung tâm kiểm soát không lưu. Xét tính đúng, sai của các mệnh đề sau:

a) Ra đa ở vị trí có tọa độ $(0; 0; 0)$.

b) Vị trí $A$ có tọa độ $(300; 200; 10)$.

c) Khoảng cách từ máy bay đến ra đa là khoảng 360,69km (làm tròn kết quả đến hàng phần trăm).

d) Ra đa của trung tâm kiểm soát không lưu không phát hiện được máy bay tại vị trí $A$.

Phần 3. Câu trả lời ngắn.

Thí sinh trả lời đáp án từ câu 1 đến câu 6.

Câu 1. Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm $t = 0(s)$ cho đến khi tên lửa đẩy được phóng đi tại thời điểm $t = 126(s)$, cho bởi hàm số sau: $v(t) = 0,001302t^3 – 0,09029t^2 + 23$ ($v$ được tính bằng $ft/s$, $1ft = 0,3048m$). Biết gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian $m(s)$ đến $126(s)$ tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi. Tìm $m$ (làm tròn kết quả đến hàng đơn vị)

Câu 2. Cho đồ thị hàm số $y = \frac{3x + 2}{x – 4}$ có đường tiệm cận đứng $x = a$ và đường tiệm cận ngang $y = b$ với $a, b \in \mathbb{Z}$. Giá trị của biểu thức $C = 5a + 6b$ là bao nhiều?

Câu 3. Hàm chi phí và hàm doanh thu (đều tính bằng triệu đồng) của một loại sản phẩm lần lượt là $C(x) = 25,5x + 1000$ và $R(x) = 75,5x$, trong đó $x$ là số đơn vị sản phẩm đó được sản xuất và bán ra. Biết hàm lợi nhuận trung bình $\overline{P}(x) = \frac{R(x) – C(x)}{x}$. Hỏi lợi nhuận trung bình sẽ không vượt quá bao nhiều triệu đồng?

Câu 4. Một con lắc lò xo, gồm một vật nặng có khối lượng 1 kg được gắn vào một lò xo được cố định một đầu, dao động điều hòa với biên độ $A = 0,24m$ và chu kì $T = 4$ giây. Vị trí $x$ (mét) của vật tại thời điểm $t$ được cho bởi $x(t) = A\cos(\omega t)$, trong đó $\omega = \frac{2\pi}{T}$ là tần số góc và thời gian $t$ tính bằng giây. Tìm thời gian tối thiểu để vật chuyển động từ vị trí ban đầu đến vị trí $x = -0,12m$ (làm tròn kết quả đến hàng phần mười).

Câu 5. Cho hai hình bình hành $ABCD$ và $ABEF$ không cùng nằm trong một mặt phẳng. Trên các đường chéo $AC$ và $BF$ lấy các điểm $M, N$ sao cho $MC = 2MA, NF = 2NB$. Khi đó biểu diễn vectơ $\overrightarrow{MN}$ theo ba vectơ $\overrightarrow{AB}, \overrightarrow{AD}, \overrightarrow{AF}$ ta được: $\overrightarrow{MN} = a \cdot \overrightarrow{AB} + b \cdot \overrightarrow{AD} + c \cdot \overrightarrow{AF}$. Tính giá trị của $12a – 3b + 6c$

Câu 6. Trong không gian với hệ tọa độ $Oxyz$, cho hình hộp $ABCD.A’B’C’D’$ có $A(4; 6; -5), B(5; 7; -4), C(5; 6; -4)$ và $D(2; 0; 2)$. Biết điểm $B'(a; b; c)$, tính $3a – b + c$?

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh