PHẦN I: Câu trắc nghiệm nhiều phương án lựa chọn.

Mỗi câu thí sinh chỉ chọn một phương án.

Câu 1: Cho hàm số $y = f(x)$ có bảng biến thiên như sau

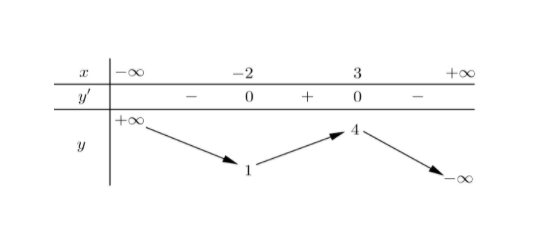
Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. $(-2; +\infty)$.

B. $(-2; 3)$.

C. $(3; +\infty)$.

D. $(-\infty; -2)$.

Câu 2: Cho hàm số $y = f(x)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên.

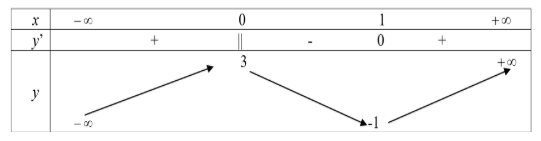
Giá trị cực tiểu của hàm số là

A. $1$.

B. $0$.

C. $3$.

D. $-1$.

Câu 3: Cho hàm số $f(x)$ có đồ thị như hình dưới đây:

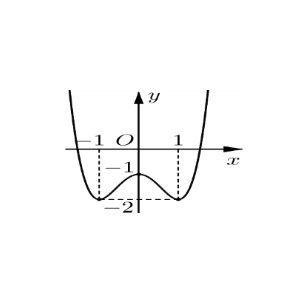
Giá trị nhỏ nhất của hàm số trên đoạn $\left[\frac{1}{2}; 1\right]$ là:

A. $-2$.

B. $-1$.

C. $0$.

D. $1$.

Câu 4: Cho hàm số $y = f(x)$ có $\lim_{x \to +\infty} f(x) = 1; \lim_{x \to -2} f(x) = -\infty$, tiệm cận ngang của đồ thị hàm số là đường nào dưới đây?

A. $y = 1$.

B. $y = -2$.

C. $x = -2$.

D. $x = 1$.

Câu 5: Cho tứ diện $ABCD$. Mệnh đề nào sau đây đúng?

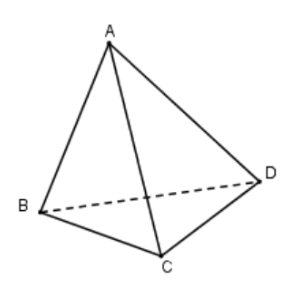
A. $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}$.

B. $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AD}$.

C. $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}$.

D. $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{CA}$.

Câu 6: Cho hình hộp $ABCD.A’B’C’D’$. Mệnh đề nào sau đây đúng?

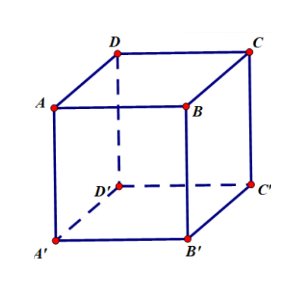
A. $\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA’} = \overrightarrow{AC’}$.

B. $\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA’} = \overrightarrow{AC’}$.

C. $\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA’} = \overrightarrow{AD’}$.

D. $\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA’} = \overrightarrow{0}$.

Câu 7: Trong không gian với hệ trục tọa độ $Oxyz$, cho $\vec{a} = -\vec{i} + 2\vec{j} – 3\vec{k}$. Tọa độ của vectơ $\vec{a}$ là

A. $(2; -1; -3)$.

B. $(2; -3; -1)$.

C. $(-1; 2; -3)$.

D. $(-3; 2; -1)$.

Câu 8: Trong không gian $Oxyz$, cho hai điểm $A(x_A; y_A; z_A)$ và $B(x_B; y_B; z_B)$. Mệnh đề nào sau đây đúng?

A. $\overrightarrow{AB} = (x_B + x_A; y_B + y_A; z_B + z_A)$.

B. $\overrightarrow{AB} = (x_B – x_A; y_B – y_A; z_B – z_A)$.

C. $\overrightarrow{AB} = (x_B.x_A; y_B.y_A; z_B.z_A)$.

D. $\overrightarrow{AB} = x_B.x_A + y_B.y_A + z_B.z_A$.

Câu 9: Trong không gian $Oxyz$, cho $\vec{a} = (x; y; z)$, $\vec{b} = (x’; y’; z’)$. Mệnh đề nào sau đây đúng?

A. $\vec{a}.\vec{b} = (x.x’; y.y’; z.z’)$

B. $\vec{a}.\vec{b} = x.x’ + y.y’ + z.z’$.

C. $\vec{a}.\vec{b} = x.x’ – y.y’ – z.z’$

D. $\vec{a}.\vec{b} = (x+x’; y+y’; z+z’)$

Câu 10: Trong không gian $Oxyz$, cho hai điểm $A(x_A; y_A; z_A)$ và $B(x_B; y_B; z_B)$. Tọa độ trung điểm của đoạn thẳng $AB$ là

A. $(x_B + x_A; y_B + y_A; z_B + z_A)$.

B. $\left(\frac{x_A-x_B}{2}; \frac{y_A-y_B}{2}; \frac{z_A-z_B}{2}\right)$.

C. $\left(\frac{x_A+x_B}{2}; \frac{y_A+y_B}{2}; \frac{z_A+z_B}{2}\right)$.

D. $(x_B – x_A; y_B – y_A; z_B – z_A)$.

Câu 11: Cho mẫu số liệu ghép nhóm thời gian sử dụng internet trong 1 tuần (giờ) của 20 học sinh như sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm trên bằng:

A. $30$.

B. $29$.

C. $25$.

D. $8$.

Câu 12: Khoảng tứ phân vị của mẫu số liệu ghép nhóm là

A. Hiệu số giữa tứ phân vị thứ ba $Q_3$ và tứ phân vị thứ nhất $Q_1$.

B. Hiệu số giữa tứ phân vị thứ ba $Q_3$ và tứ phân vị thứ hai $Q_2$.

C. Hiệu số giữa tứ phân vị thứ nhất $Q_1$ và tứ phân vị thứ ba $Q_3$.

D. Hiệu số giữa tứ phân vị thứ hai $Q_2$ và tứ phân vị thứ nhất $Q_1$

PHẦN II: Câu trắc nghiệm đúng sai.

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Cho hàm số $y = f(x) = \frac{x+1}{x-3}$.

a) Tập xác định của hàm số là $\mathbb{R} \setminus {3}$.

b) $y’ = \frac{-4}{(x-3)^2}$.

c) đường tiệm cận đứng của đồ thị hàm số là $y = 3$.

d) Số đường tiệm cận của đồ thị hàm số là $2$.

Câu 2: Cho hình lập phương $ABCD.A’B’C’D’$ có cạnh bằng 3 như hình bên.

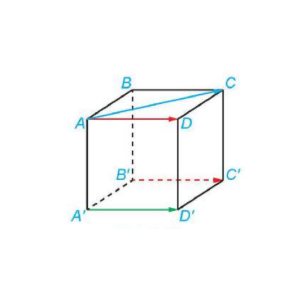
a) $\overrightarrow{AB} = \overrightarrow{D’C’}$.

b) Góc giữa hai vector $\overrightarrow{AC}$ và $\overrightarrow{D’C’}$ bằng $60°$.

c) $|\overrightarrow{AC}| = 3\sqrt{2}$.

d) Tích vô hướng $\overrightarrow{AC}.\overrightarrow{D’C’} = 6$.

Câu 3: Trong không gian $Oxyz$, cho hai vector $\vec{a} = (2; -1; 3)$ và $\vec{b} = \vec{i} – 5\vec{j} + 2\vec{k}$.

a) $\vec{b} = (1; -5; 2)$.

b) $|\vec{a}| = \sqrt{14}$.

c) $\vec{a} – 2\vec{b} = (4; -11; -1)$.

d) Hai vector $\vec{a}$ và $\vec{b}$ vuông góc với nhau.

Câu 4: Thời gian sử dụng internet (tính theo giờ) của bạn An trong 20 ngày nghỉ hè đầu tiên được thống kê như sau:

a) Khoảng biến thiên của mẫu số liệu ghép nhóm là $R = 2,5$

b) Nhóm chứa tứ phân vị thứ ba là nhóm $[2; 2,5)$.

c) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là $Q_1 = \frac{4}{3}$

d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là $\Delta_Q = 1$.

PHẦN III: Câu trắc nghiệm trả lời ngắn.

Câu 1: Một máy bay loại nhỏ bắt đầu hạ cánh, đường bay của nó gần với hệ trục tọa độ $Oxy$ được mô phỏng ở hình bên dưới. Đường bay của nó có dạng là một phần của đồ thị hàm số bậc ba $y = ax^3 + bx^2 + cx + d(a \neq 0)$ với $x \in [-4; 0]$, vị trí bắt đầu hạ cánh có tọa độ $(-4; 1)$ là điểm cực đại của đồ thị hàm số và máy bay tiếp đất tại vị trí có tọa độ là điểm cực tiểu của đồ thị hàm số.

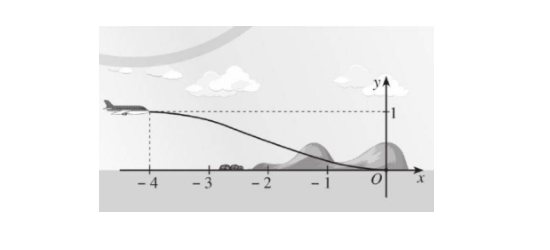
Tính $a \cdot \frac{1}{a} + c + d$.

Câu 2: Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C như hình bên dưới. Khoảng cách từ C đến B là 4km. Bờ biển chạy thẳng từ A đến B với khoảng cách là 10km. Giá sử chi phí lắp đặt 1km dây điện trên bờ biển là 50 triệu đồng, còn trên đáy liền là 30 triệu đồng.

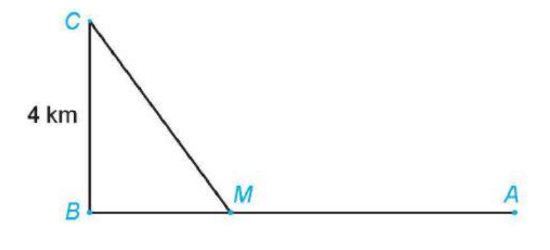
Khi tổng chi phí lắp đặt là nhỏ nhất thì khoảng cách giữa điểm M (điểm nối dây từ đất liền ra đảo) và điểm A là $a(km)$. Tìm $a$.

Câu 3: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $3$, $SA \perp (\mathrm{ABCD})$, $SA = 5$ (Hình vẽ bên dưới).

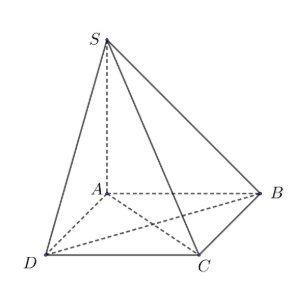
Biết $|\overrightarrow{AB} + \overrightarrow{AD}| = a\sqrt{b}$. Tính $a + b$.

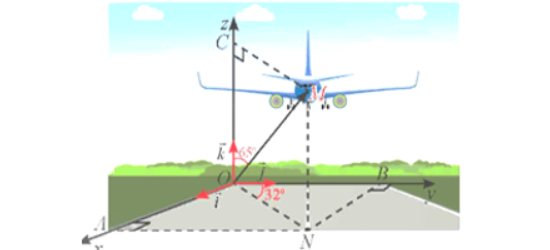
Câu 4: Một máy bay đang cất cánh từ phi trường. Với hệ tọa độ $Oxyz$ được thiết lập như hình vẽ bên dưới, cho biết M là vị trí của máy bay, $OM = 14$, $\widehat{MOB} = 32°$, $\widehat{MOC} = 65°$. Giả sử $M(x; y; z)$ (kết quả $x, y, z$ làm tròn đến chữ số thập phân thứ nhất). Tính $S = x + y + z$.

Câu 5: Trong không gian $Oxyz$, cho hai điểm $A(4; -1; 2)$, $B(7; 3; 2)$. Gọi $M(b; b; c)$ là điểm trên mặt phẳng $(Oxz)$ sao cho tam giác $ABM$ vuông cân tại $A$. Tính $2b + 3c$.

Câu 6: Bảng dưới đây thống kê cự li ném tạ 100 lần của một vận động viên.

Hãy tính phương sai của mẫu số liệu ghép nhóm trên (Làm tròn đến hàng phần trăm).

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh