PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.

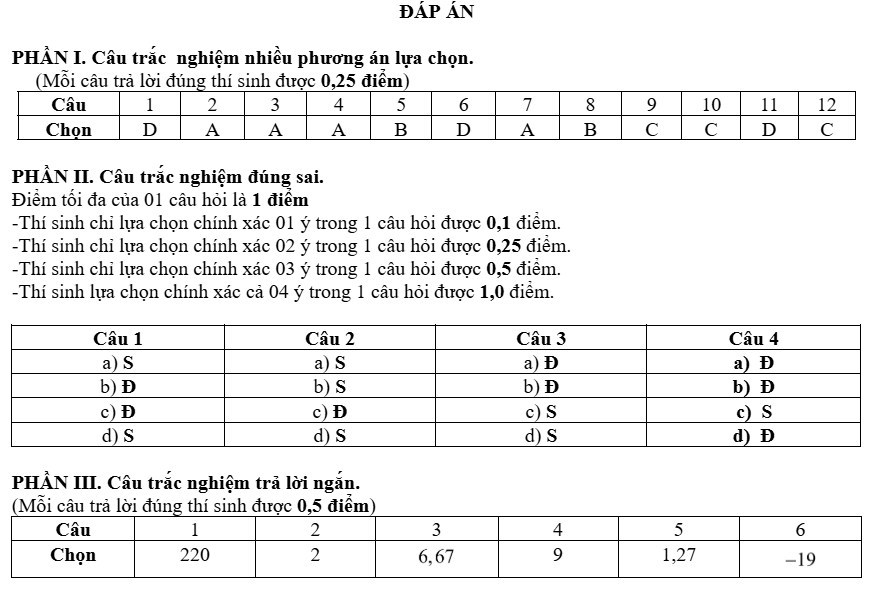
Câu 1: Cho hàm số $y = f(x)$ có đồ thị như hình vẽ. Hàm số $y = f(x)$ đồng biến trên khoảng nào dưới đây

A. $(-\infty; 0)$

B. $(-2; 2)$.

C. $(2; +\infty)$

D. $(0; 2)$

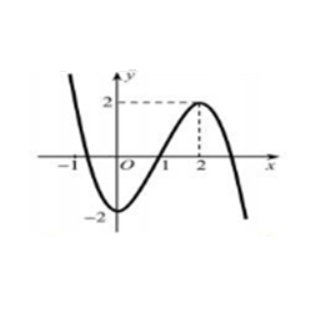
Câu 2: Cho hàm số $y = f(x)$ liên tục trên đoạn $[-2; 4]$ và có đồ thị như hình vẽ bên. Giá trị nhỏ nhất của hàm số $y = f(x)$ là

A. $-3$.

B. $1$.

C. $2$.

D. $6$.

Câu 3: Tiệm cận đứng của đồ thị hàm số $y = \frac{2x-1}{x-1}$ là đường thẳng có phương trình:

A. $x = 1$.

B. $x = -1$.

C. $x = 2$.

D. $x = \frac{1}{2}$.

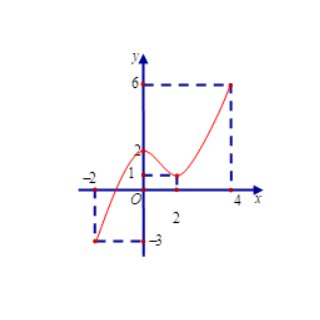
Câu 4: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên dưới?

A. $y = -2x^4 + 4x^2 – 1$.

B. $y = -x^3 + 3x – 1$.

C. $y = 2x^4 – 4x^2 – 1$.

D. $y = x^3 – 3x – 1$.

Câu 5: Cho hình lập phương $ABCD.A’B’C’D’$ có tâm $O$. Gọi $I$ là tâm của hình vuông $A’B’C’D’$ và $M$ là điểm thuộc đoạn thẳng $OI$ sao cho $OM = \frac{1}{2}MI$ (tham khảo hình vẽ).

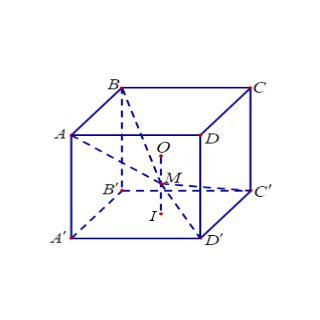
Khẳng định nào sau đây là đúng?

A. $3\overrightarrow{IM} = \overrightarrow{OI}$.

B. $\overrightarrow{MO} = \frac{1}{2}\overrightarrow{MI}$.

C. $\overrightarrow{OM} = \overrightarrow{MI}$.

D. $\overrightarrow{MI} = 2\overrightarrow{MO}$

Câu 6: Trong không gian $Oxyz$, cho hai điểm $A(1; 1; -2)$ và $B(2; 2; 1)$. Vectơ $\overrightarrow{AB}$ có tọa độ là

A. $(3; 3; -1)$.

B. $(-1; -1; -3)$.

C. $(3; 3; 1)$

D. $(1; 1; 3)$.

Câu 7: Khảo sát chiều cao của một nhóm 10 học sinh lớp 12A (theo đơn vị đo là centimet). Ta có được mẫu số liệu ghép nhóm như sau:

Khoảng biến thiên của mẫu số liệu trên là

A. $20$.

B. $25$.

C. $15$.

D. $30$.

Câu 8: Cho mẫu số liệu ghép nhóm về tuổi thọ của 10 người dân trong khu chung cư như sau:

Trung bình của mẫu số liệu ghép nhóm trên là

A. $75$.

B. $76$.

C. $75,5$.

D. $76,5$.

Câu 9: Giá trị cực đại của hàm số $y = -x^3 + 3x$ là

A. $0$.

B. $1$.

C. $2$.

D. $-2$.

Câu 10: Một vật chuyển động theo quy luật $s = -\frac{1}{2}t^3 + 6t^2$ với $t$ (giây) là khoảng thời gian từ khi vật bắt đầu khởi động và $s$ (mét) là quãng đường vật đi chuyển trong thời gian đó. Vận tốc đạt được tại thời gian $6$ giây là

A. $24$ (m/s).

B. $12$ (m/s).

C. $18$ (m/s).

D. $23$ (m/s).

Câu 11: Số tiệm cận đứng của đồ thị hàm số $y = \frac{\sqrt{x+16}-4}{x^2+x}$ là

A. $0$.

B. $3$.

C. $2$.

D. $1$.

Câu 12: Trong không gian $Oxyz$, cho điểm $A(1; 2; -3)$. Điểm đối xứng của $A$ qua mặt phẳng $(Oxy)$ có tọa độ là

A. $(1; 0; -3)$.

B. $(1; 0; 0)$.

C. $(1; 2; 3)$.

D. $(0; 2; -3)$.

PHẦN II. Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S).

Câu 1: Thể tích nước của một bể bơi sau $t$ phút bơm được tính theo công thức $V(t) = \frac{1}{100}\left(30t^2 – \frac{t^3}{4}\right)$ ($m^3$) $(0 \leq t \leq 90)$. Tốc độ bơm nước tại thời điểm $t$ được tính bởi $v(t) = V'(t)$.

a) Thể tích nước sau $10$ phút là $80(m^3)$.

b) Tốc độ bơm nước tại thời điểm $t = 20$ phút là $280(m^3/phút)$.

c) Sau $60$ phút, tốc độ bơm nước giảm.

d) Tốc độ bơm nước cao nhất là $1000(m^3/phút)$.

Câu 2: Cho hàm số $y = \frac{3x-1}{2x-1}$ có đồ thị $(C)$. Các mệnh đề sau đúng hay sai?

a) Đạo hàm: $y’ = \frac{-5}{(2x-1)^2}$.

b) Hàm số đồng biến trên trên $\left(-\infty; \frac{1}{2}\right)$ và $\left(\frac{1}{2}; +\infty\right)$.

c) Đồ thị $(C)$ có tiệm cận ngang là $y = \frac{3}{2}$; tiệm cận đứng $x = \frac{1}{2}$.

d) Đồ thị $(C)$ cắt trục $Oy$ tại điểm có tung độ $y = 0$.

Câu 3: Hai chiếc flycam được điều khiển cùng bay lên tại một địa điểm. Sau một thời gian bay, chiếc flycam thứ nhất cách mặt đất $5m$, cách điểm xuất phát $3m$ về phía Nam và $2m$ về phía Đông. Chiếc flycam thứ hai cách mặt đất $5m$, cách điểm xuất phát $6m$ về phía Bắc và $6m$ về phía Tây. Chọn hệ trục tọa độ $Oxyz$ với gốc $O$ đặt tại điểm xuất phát của hai chiếc flycam, mặt phẳng $(Oxy)$ trùng với mặt đất có trục $Ox$ hướng về phái nam, trục $Oy$ hướng về phía đông và trục $Oz$ hướng thẳng đứng lên trời, đơn vị đo lấy theo mét.

Các mệnh đề sau đúng hay sai?

a) Tọa độ của chiếc flycam thứ nhất là $A(3; 2; 5)$. Tọa độ của chiếc flycam thứ hai là $B(-6; -6; 5)$

b) Điểm đối xứng của $A$ qua mặt phẳng tọa độ $(Oxy)$ là $A(3; 2; -5)$

c) Tọa độ điểm $M$ thuộc mặt phẳng $(Oxy)$ sao cho $M, A, B$ thẳng hàng là $M(-9; -8; 10)$

d) Trên mặt đất, người ta xác định một vị trí sao cho tổng khoảng cách từ đó đến hai chiếc flycam ngắn nhất. Khoảng cách từ điểm xuất phát đến vị trí đó là $7\sqrt{5}$

Câu 4: Giá động của cửa một cổ phiếu là giá của cổ phiếu đó cuối một phiên giao dịch. Bảng sau thống kê giá đóng cửa (đơn vị: nghìn đồng) của hai mã cổ phiếu $A$ và $B$ trong 50 ngày giao dịch liên tiếp.

a) Cỡ mẫu của cổ phiếu $A$ là 50

b) Xét mẫu số liệu của cổ phiếu $A$ ta có phương sai của mẫu số liệu ghép nhóm là $7,5216$

c) Xét mẫu số liệu của cổ phiếu $B$ ta có số trung bình của mẫu số liệu ghép nhóm là $115,28$.

d) Người ta có thể dùng phương sai và độ lệch chuẩn để so sánh mức độ rủi ro của các loại cổ phiếu có giá trị trung bình gần bằng nhau. Cổ phiếu nào có phương sai, độ lệch chuẩn cao hơn thì được coi là có độ rủi ro lớn hơn. Theo quan điểm trên, thì cổ phiếu $A$ có độ rủi ro thấp hơn cổ phiếu $B$.

PHẦN III. Câu trắc nghiệm trả lời ngắn.

Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: Hai chiếc khinh khí cầu cùng bay lên tại một địa điểm. Sau một giờ bay, chiếc khinh khí cầu thứ nhất cách điểm xuất phát về phía Đông $100$ (km) và về phía Nam $80$ (km), đồng thời cách mặt đất $1$ (km). Chiếc khinh khí cầu thứ hai cách điểm xuất phát về phía Bắc $70$ (km) và về phía Tây $60$ (km), đồng thời cách mặt đất $10$ (km). Xác định khoảng cách (km) giữa hai chiếc khinh khí cầu.

Câu 2: Trong không gian $Oxyz$, cho hai điểm $A(1; 2; 1)$, $B(2; -1; 3)$ và điểm $M(a; b; 0)$ sao cho $MA^2 + MB^2$ nhỏ nhất. Giá trị của $a + b$ bằng bao nhiều?

Câu 3: Khi nồi vật là mặc kệt trong khí quyển thì phải hỏ, có hoạnh đây lên trên gây ra tăng áp trong nồi. Theo lí thuyết, áp suất hơi nước có thể làm nền khí quyển khiển không khí đủ qua mạnh hơn. Đối với một lượng không khí bị đậy ra trong một không khí có định, khí quyển càng nho thì lượng không khí càng đẩy ra nhanh hơn. Vận tốc lượng khí thoát ra càng cao, lực tác động lên vật là càng lớn. Qua nghiên cứu một số trường hợp, người ta nhận thấy vận tốc $v$ của lượng khí liên hệ với bán kính $x$ của khí quyển theo công thức: $v(x) = (x_0 – x)x^2$ với $\frac{1}{2} \leq x \leq x_0$.

Trong đó $x_0$ là bán kính khí quyển ở trạng thái bình thường. Xét một người trường thành sức khỏe tốt có bán kính khí quyển ở trạng thái bình thường bằng $10mm$. Tìm $x$ để vận tốc của lượng khí mỗi con hơ trong trường hợp này là lớn nhất (tính bằng đơn vị $mm$, làm tròn đến hàng phần trăm).

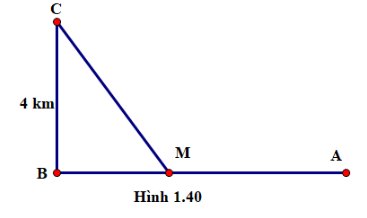
Câu 4: Một đường dây điện được nối từ một nhà máy điện ở $A$ đến một hòn đảo ở $C$ như Hình 1.40. Khoảng cách từ hòn đảo $C$ đến bờ biển là đoạn $CB = 4km$. Bờ biển chạy thẳng từ $A$ đến $B$ với khoảng cách là $12km$. Tổng chi phí lắp đặt cho 1 km dây điện trên biển là 50 triệu đồng, còn trên đất liền là 30 triệu đồng. Hỏi cần đặt vị trí nối dây $M$ trên đoạn AB (điểm nối dây từ đất liền ra đảo) cách nhìu km từ điểm A bao nhiêu km để tổng chi phí lắp đặt là nhỏ nhất.

Câu 5: Một người chèo một chiếc thuyền xuất phát từ điểm $A$ trên bờ một con sông thẳng rộng $2km$, và muốn đến điểm $B$ cách bờ đối diện $10km$. Người này có thể chỉ chèo thuyền hoặc kết hợp chèo thuyền với chạy bộ, càng nhanh càng tốt. Chẳng hạn, anh ta có thể chèo thuyền qua sông đến điểm $C$ rồi chạy bộ đến điểm $A$, hoặc anh ta có thể chèo thuyền thẳng đến $B$, hoặc anh ta có thể chèo thuyền qua sông đến điểm $D$ nào đó ở giữa $C$ và $B$ rồi chạy bộ đến điểm $B$ (hình minh họa). Biết rằng vận tốc chèo thuyền của anh là $6km/h$ (đã tính vận tốc dòng nước), vận tốc chạy bộ của anh là $10km/h$. Trong tất cả các phương án đến $B$ bằng cách chèo thuyền hoặc chèo thuyền rồi chạy bộ, phương án nhanh nhất có tổng thời gian là bao nhiều giờ? Làm tròn kết quả đến hàng phần trăm.

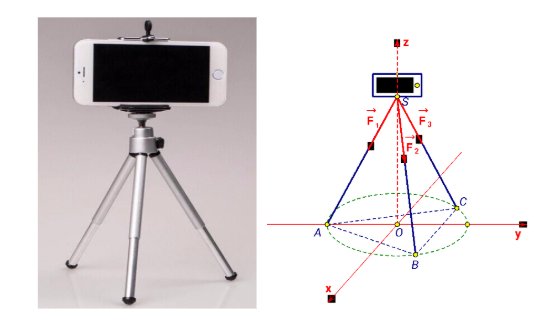
Câu 6: Một chiếc điện thoại Iphone được đặt trên một giá đỡ có ba chân với điểm đặt $S(0; 0; 20)$ và các điểm chạm mặt đất của ba chân lần lượt là $A(0; -6; 0)$, $B(3\sqrt{3}; 3; 0)$, $C(-3\sqrt{3}; 3; 0)$ (đơn vị cm). Cho biết điện thoại có trọng lượng là $2N$ và ba lực tác dụng lên giá đỡ được phân bố như hình vẽ là ba lực $\overrightarrow{F_A}, \overrightarrow{F_B}, \overrightarrow{F_C}$ có độ lớn bằng nhau. Biết tọa độ của lực $\overrightarrow{F_A} = (a; b; c)$, khi đó $T = 2a – 5b + 30c$ bằng?

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh