Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
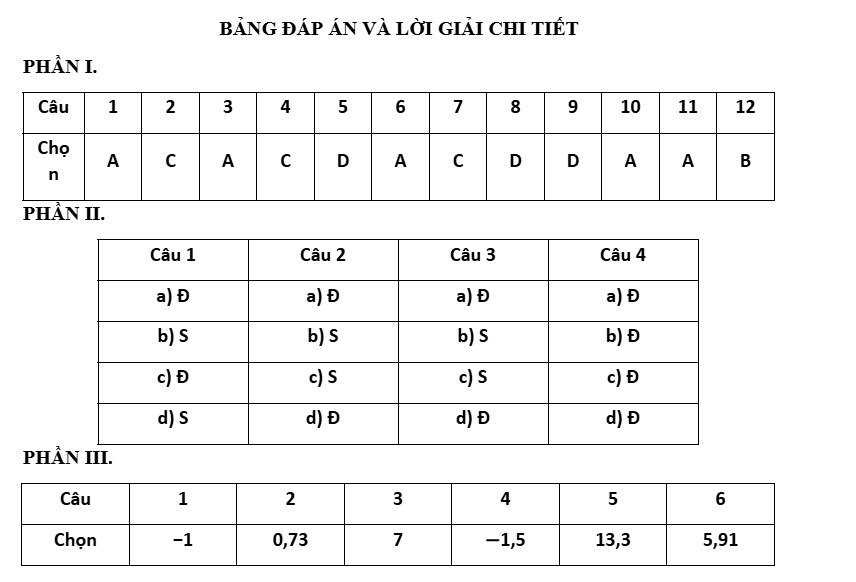
Câu 1: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A. $y = x^3 – 2024x$.
B. $y = -x^3 + 3x$.
C. $y = x^3 – 3x^2 + 2024$
D. $y = -x^3 + 3x^2 – 2$.
Câu 2: Đồ thị hàm số $y = \frac{x+1}{x^2+x-2}$ có bao nhiều đường tiệm cận đứng?
A. $1$.
B. $3$.
C. $2$.
D. $4$.
Câu 3: Giá trị lớn nhất của hàm số $f(x) = x + \frac{4}{x}$ trên $(-4; 0)$ là
A. $-4$.
B. $4$.
C. $-5$.
D. $5$.
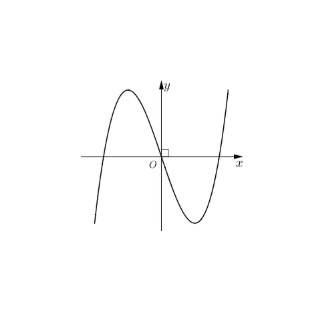
Câu 4: Cho hàm số $y = \frac{x^2 + a}{x + b}$ có đồ thị là đường cong trong hình vẽ bên. Giá trị của $T = a + b$ bằng
A. $T = 0$.
B. $T = -2$.
C. $T = -1$.
D. $T = 2$.
Câu 5: Cho hình lập phương $ABCD.A’B’C’D’$. Hai vectơ nào có giá cùng nằm trong mặt phẳng $(ABCD)$.
A. $\overrightarrow{DD’}, \overrightarrow{AC}$.
B. $\overrightarrow{AD’}, \overrightarrow{AB}$
C. $\overrightarrow{AD’}, \overrightarrow{AC}$.
D. $\overrightarrow{AC}, \overrightarrow{AD}$.
Câu 6: Trong không gian $Oxyz$, cho biểu diễn của vectơ $\vec{a}$ qua các vectơ đơn vị là $\vec{a} = 2\vec{i} + \vec{k} – 3\vec{j}$. Tọa độ của vectơ $\vec{a}$ là
A. $(2; -3; 1)$.
B. $(1; -3; 2)$.
C. $(2; 1; -3)$.
D. $(1; 2; -3)$
Câu 7: Trong không gian với hệ tọa độ $Oxyz$, cho điểm $M(4; 1; -2)$ và vectơ $\vec{u} = (4; -2; 6)$. Tìm tọa độ điểm $N$ biết rằng $\overrightarrow{MN} = -\frac{1}{2}\vec{u}$.
A. $(2; 2; 5)$.
B. $(2; -2; 5)$.
C. $(2; 2; -5)$.
D. $(-2; -2; 5)$.
Câu 8: Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Chọn phát biểu đúng.
A. $\overrightarrow{SD} – \overrightarrow{SA} = \overrightarrow{DA}$.
B. $\overrightarrow{SC} – \overrightarrow{SD} = \overrightarrow{CD}$.
C. $\overrightarrow{SB} – \overrightarrow{SA} = \overrightarrow{BA}$.
D. $\overrightarrow{SD} – \overrightarrow{SA} = \overrightarrow{AD}$.
Câu 9: Trong không gian $Oxyz$, cho $A(4; 0; 0)$, $B(0; 2; 0)$. Tâm đường tròn ngoại tiếp tam giác $OAB$
A. $I(2; -1; 0)$.
B. $I\left(\frac{4}{3}; \frac{2}{3}; 0\right)$.
C. $I(-2; 1; 0)$.
D. $I(2; 1; 0)$.
Câu 10: Trong không gian $Oxyz$, cho ba điểm $A(3; 5; -1)$, $B(7; x; 1)$ và $C(9; 2; y)$. Để $A, B, C$ thẳng hàng thì giá trị $x + y$ bằng
A. $5$.
B. $6$.
C. $4$.
D. $7$.
Câu 11: Cô Hà thống kê lại đường kính thân gỗ của một số cây xoan đào 6 năm tuổi được trồng ở một làm trường ở bảng sau.

Hãy tìm khoảng biến thiên của mẫu số liệu ghép nhóm trên.
A. $25$.
B. $30$.
C. $6$.
D. $69,8$.
Câu 12: Thời gian (phút) truy bài trước mỗi buổi học của một số học sinh trong một tuần được ghi lại ở bảng sau:

Nhóm chứa tứ phân vị thứ nhất là
A. $[9,5; 12,5)$.
B. $[12,5; 15,5)$.
C. $[15,5; 18,5)$.
D. $[18,5; 21,5)$.
PHẦN II. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
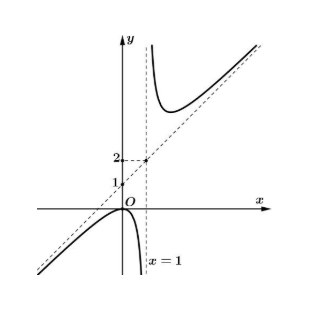
Câu 1: Cho hàm số $y = f(x)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ:
a) Hàm số đồng biến trên khoảng $(0; 2)$.
b) Hàm số đạt cực đại tại $x = 0$.
c) Giá trị nhỏ nhất của hàm số trên $[-1; 1]$ bằng $-4$.
d) Hàm số $g(x) = f(3 – x)$ nghịch biến trên $(2; 5)$.
Câu 2: Dân số của một quốc gia sau t (năm) kể từ năm 2023 được ước tính bởi công thức: $N(t) = 100.e^{0,03t}$, $N(t)$ được tính bằng triệu người, $0 \leq t \leq 50$.
a) Ước tính dân số của quốc gia này vào năm 2030 là 108,763 triệu người. (kết quả làm tròn kết quả đến chữ số thập phân thứ ba).
b) Ước tính dân số của quốc gia này vào năm 2035 là 145,488 triệu người. (kết quả làm tròn kết quả đến chữ số thập phân thứ ba).
c) Xem $N(t)$ là hàm số của biến số $t$ xác định trên đoạn $[0; 50]$. Hàm số $N(t)$ luôn nghịch biến trên đoạn $[0; 50]$.
d) Đạo hàm của hàm số $N(t)$ biểu thị tốc độ tăng dân số của quốc gia đó (tính bằng triệu người/năm). Vào năm 2046 tốc độ tăng dân số của quốc gia đó là 1,6 triệu người/năm.
Câu 3: Hình minh họa sơ đồ một ngôi nhà trong không gian $Oxyz$, trong đó nền nhà, bốn bức tường và hai mái nhà đều là hình chữ nhật. Xét tính đúng sai các mệnh đề sau:
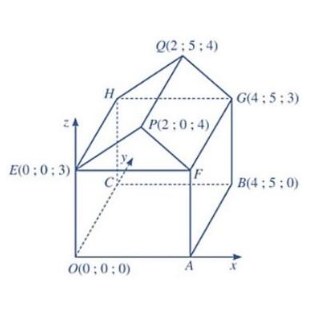
a) Tọa độ điểm $F(4; 0; 3)$
b) Tọa độ vectơ $\overrightarrow{AH} = (4; 5; 3)$.
c) $\overrightarrow{AH}.\overrightarrow{AF} = 3$.
d) Góc độ của mái nhà, tức là số đo của góc thị điều có cạnh là đường thẳng $FG$, hai mặt lân lượt là $(FGOP)$ và $(FGHE)$ bằng $26,6°$ (làm tròn kết quả đến hàng phần mười).
Câu 4: Kết quả môn Toán (cùng độ) của học sinh hai lớp 12A và 12B được cho lần lượt bởi mẫu số liệu ghép nhóm ở bảng sau:
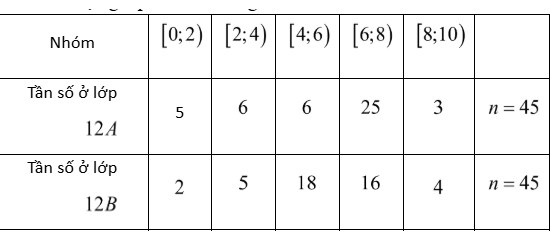
a) Số trung bình cộng của hai mẫu số liệu trên bằng nhau.
b) Độ lệch chuẩn của mẫu số liệu lớp 12A nhỏ hơn $3$.
c) Phương sai của mẫu số liệu lớp 12B lớn hơn $3$.
d) Điểm thí của học sinh lớp 12B đồng đều hơn lớp 12A.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời câu 1 đến câu 6.
Câu 1:
Tiệm cận xiên của đồ thị hàm số $y = f(x) = \frac{3x-1}{2x-1}$ là đường thẳng $y = ax + b$.
Tính giá trị của biểu thức $P = a^2 – b$.
Câu 2:
Chi Hà dự định sử dụng hết $4m^2$ kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp (chiều dài gấp đôi chiều rộng (các mép ghép có thể không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu mét khối (kết quả làm tròn đến hàng phần trăm)?
Câu 3:
Quan sát một dân ong trong 20 tuần, người ta ước lượng được số lượng ong trong đàn bởi công thức $P(t) = \frac{20000}{1+1000e^{-t}}$, trong đó $t$ là thời gian tính theo tuần kể từ khi bắt đầu quan sát, $0 \leq t \leq 20$. Tại thời điểm nào thì số lượng ong của đàn tăng nhanh nhất (kết quả làm tròn đến hàng đơn vị của tuần).
Câu 4:
Trong một căn phòng dạng hình hộp chữ nhật với chiều dài $8m$, rộng $6m$ và cao $4m$ có $2$ cây quạt treo tường. Cây quạt $1$ treo chính giữa bức tường $8m$ và cách trần $1m$, cây quạt $B$ treo chính giữa bức tường $6m$ và cách trần $1.5m$. Chọn hệ trục tọa độ $Oxyz$ như hình vẽ bên dưới (1 đơn vị: mét). Giả sử $\overrightarrow{AB} = (a;b;c)$. Tính $a + b + c$.

Câu 5:
Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật $ABCD$, mặt phẳng $(ABCD)$ song song với mặt phẳng năm ngang. Khung sắt đó được buộc vào móc E của chiếc cần cẩu sao cho các đoạn dây cáp $EA, EB, EC$ và $ED$ có độ dài bằng nhau và cùng tạo với mặt phẳng $(ABCD)$ một góc bằng $60°$ (hình minh họa). Chiếc cần cẩu dạng kéo khung sắt lên theo phương thẳng đứng.
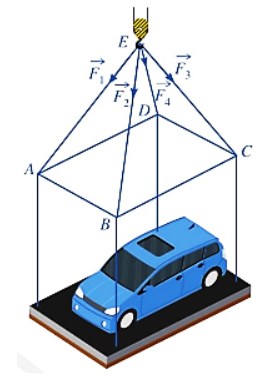
Biết rằng các lực căng $\vec{F_1}, \vec{F_2}, \vec{F_3}, \vec{F_4}$ đều có cường độ là $4.7 kN$ và trọng lượng của khung sắt là $3 kN$. Trọng lượng lớn nhất của chiếc xe ô tô (làm tròn đến hàng phần mười) là bao nhiêu kN?
Câu 6:
Chiều dài của 40 bé sơ sinh 12 ngày tuổi được chọn ngẫu nhiên ở viện nhi trung ương được cho trong bảng thống kê dưới đây:

Tìm phương sai (làm tròn đến hàng phần trăm) của 40 bé sơ sinh ở bảng thống kê trên.

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh