PHẦN I. Câu trắc nghiệm với nhiều phương án lựa chọn

Câu 1: Thời gian tập luyện trong một ngày (tính theo giờ) của một số vận động viên được ghi lại ở bảng sau:

Nhóm chứa tứ phân vị thứ hai là

A. $[2;4)$.
B. $[4;6)$.
C. $[6;8)$.
D. $[8;10)$.

Câu 2: Cho hàm số $y = f(x)$ có đồ thị $f'(x)$ là đường cong hình bên dưới. Hàm số $y = f(x)$ đồng biến trên khoảng nào dưới đây?

A. $(0;2)$.
B. $(-4;2)$.
C. $(2;+\infty)$.
D. $(-\infty;-1)$.

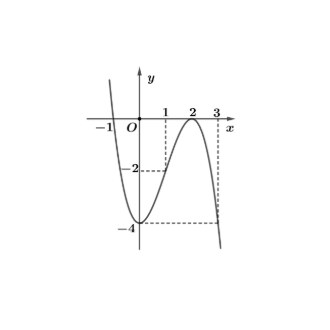
Câu 3: Cho hàm số $f(x)$ liên tục trên đoạn $[-2;2]$ có đồ thị như hình vẽ. Gọi $M$ và $m$ lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn $[-2;2]$. Khi đó, tổng $M + m$ bằng

A. $-6$.
B. $-2$.
C. $-5$.
D. $2$.

Câu 4: Giá trị lớn nhất của hàm số $f(x) = \frac{x^2 + 3}{x + 1}$ trên đoạn $[0; 2]$ là

A. $2$.
B. $3$.
C. $\frac{7}{3}$.
D. $\frac{10}{3}$.

Câu 5: Đồ thị hàm số $y = \frac{2x – 1}{x – 1}$ có tiệm cận đứng là đường thẳng

A. $x = 2$.
B. $y = 2$.
C. $y = 1$.
D. $x = 1$.

Câu 6: Hàm số nào sau đây có đồ thị như hình vẽ?

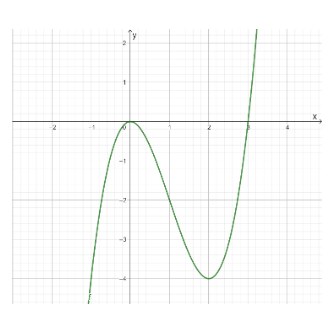
A. $y = -x^3 – 3x^2$.
B. $y = x^3 – 3x^2$.
C. $y = x^3 + 3x^2$.
D. $y = -x^3 + 3x^2$.

Câu 7: Trong không gian $Oxyz$, vectơ $\vec{u} = (2; 1; -1)$ không định nào sau đây đúng?

A. $\vec{u} = 2\vec{i} – \vec{j} + \vec{k}$.
B. $\vec{u} = 2\vec{i} + \vec{j} + \vec{k}$.
C. $\vec{u} = -2\vec{i} – \vec{j} + \vec{k}$.
D. $\vec{u} = 2\vec{i} + \vec{j} – \vec{k}$.

Câu 8: Kết quả khảo sát cân nặng của $25$ quả cam ở một lô hàng được cho dưới bảng sau:

Phương sai của mẫu số liệu ghép nhóm trên gần bằng

A. $s^2 = 17,1246$.
B. $s^2 = 17,2264$.
C. $s^2 = 21,36$.
D. $s^2 = 17,1264$.

Câu 9: Trong không gian $Oxyz$, cho $\vec{a} = 4\vec{k} – 3\vec{j} + \vec{i}$. Khi đó, tọa độ vectơ $\vec{a}$ bằng

A. $\vec{a} = (4; -3; 1)$.
B. $\vec{a} = (-3; 4; 1)$.
C. $\vec{a} = (1; -3; 4)$.
D. $\vec{a} = (4; 1; -3)$.

Câu 10: Trong không gian với hệ trục tọa độ $Oxyz$, cho hai vectơ $\vec{a} = (5; 3; -2)$ và $\vec{b} = 2\vec{i} – \vec{j} + 3\vec{k}$. Tìm tọa độ của $\vec{u} = 2\vec{a} + 3\vec{b}$

A. $\vec{u} = (10; 6; -4)$.
B. $\vec{u} = (16; 3; 5)$.
C. $\vec{u} = (16; 9; 5)$.
D. $\vec{u} = (10; -3; -6)$.

Câu 11: Trong không gian $Oxyz$, cho ba điểm $A(2; -2; 4)$, $B(-3; 3; -1)$, $C(-1; -1; -1)$. Tọa độ điểm $I(a; b; c)$ thỏa mãn $2\vec{IA} + \vec{IB} – \vec{IC} = \vec{0}$. Tính $a + b + c$.

A. $4$.
B. $5$.
C. $6$.
D. $3$.

Câu 12: Trong không gian với hệ trục $Oxyz$ cho ba điểm $A(-1; 2; -3)$, $B(1; 0; 2)$, $C(x; y; -2)$ thẳng hàng. Khi đó $x + y$ bằng

A. $x + y = 1$.
B. $x + y = 17$.
C. $x + y = -\frac{11}{5}$.
D. $x + y = \frac{11}{5}$.

PHẦN II. Câu trắc nghiệm đúng sai

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ có đạo hàm $f'(x) = x(x+1)^{2025}(x-3)^{2024}, \forall x \in \mathbb{R}$. Biết $f(0) = 0$. Xét tính đúng sai của các khẳng định sau:

a) Hàm số $y = f(x)$ đồng biến trên khoảng $(0;3)$.

b) Hàm số $y = f(x)$ đạt cực đại tại $x = 0$.

c) Hàm số có hai cực trị trái dấu.

d) Đồ thị hàm số $y = \frac{1}{f(x)}$ có 3 đường tiệm cận đứng.

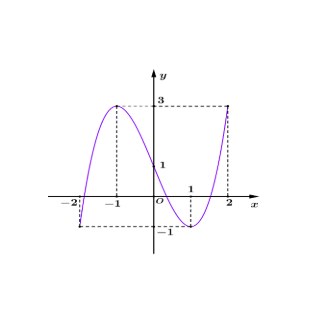
Câu 2: Cho hàm số $y = f(x)$ có đồ thị $(C)$ như hình vẽ bên dưới:

a) Đồ thị $(C)$ cắt trục $Oy$ tại điểm có tung độ bằng $2$.

b) Đồ thị hàm số $(C)$ nhận $I(4;1)$ là tâm đối xứng.

c) Hàm số $y = f(x)$ có hai cực trị trong đó $y_{C_T} > y_{C_\Gamma}$.

d) Hai đường tiệm cận của đồ thị cùng với trục hoành tạo thành tam giác có diện tích bằng $2$.

Câu 3: Trong không gian, cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $O$. Gọi $G$ là điểm thỏa mãn $\overrightarrow{GS} + \overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} + \overrightarrow{GD} = \vec{0}$ (tâm khối lăng thể)

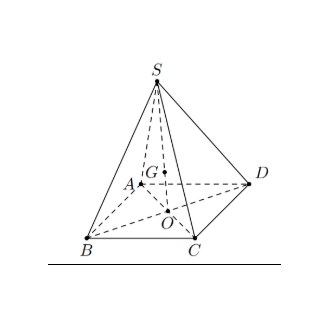
a. Hai vectơ $\overrightarrow{AO}, \overrightarrow{CO}$ bằng nhau.

b. $\overrightarrow{SB} + \overrightarrow{SD} = \overrightarrow{SA} + \overrightarrow{SC}$

c. $\overrightarrow{GS} = 4\overrightarrow{OG}$

d. Nếu tam giác $\triangle ABC$ có $AB = 2a, BC = a\sqrt{7}, AC = 3a$ thì $\overrightarrow{AB}.\overrightarrow{AC} = 3a^2$

Câu 4: Điểm kiểm tra cuối kỳ I môn Toán của 36 học sinh lớp 12D1 tại một trường THPT được ghi lại ở bảng sau:

a) Khoang biến thiên của mẫu số liệu bằng 10.

b) Nếu so sánh theo số trung bình thì học sinh lớp 12D1 có điểm trung bình lớn hơn 5 điểm.

c) Khoảng tứ phân vị của mẫu số liệu không vượt quá 2.

d) Số học sinh có điểm số lớn hơn 1.

PHẦN III. Câu trắc nghiệm trả lời ngắn

Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: Cho hình hộp $ABCD.A_1B_1C_1D_1$. Tìm giá trị của $k$ thích hợp điền vào đẳng thức vectơ: $\overrightarrow{AB} + \overrightarrow{B_1C_1} + \overrightarrow{DD_1} = k\overrightarrow{AC_1}$.

Câu 2: Người quản lí của một khu chung cư có 100 căn hộ cho thuê nhận thấy rằng tất cả các căn hộ sẽ có người thuê nếu giá thuê một căn hộ là 8 triệu đồng một tháng. Một cuộc khảo sát thị trường cho thấy rằng, trung bình cứ mỗi lần tăng giá thuê căn hộ thêm 100 nghìn đồng thì sẽ có thêm một căn hộ bị bỏ trống. Người quản lí nên đặt giá thuê (triệu) mỗi căn hộ là bao nhiêu để doanh thu là lớn nhất?

Câu 3: Ông A dự định sử dụng hết $5,5m^2$ kính để làm một bể cá có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?

Câu 4: Trong không gian Oxyz (đơn vị trên mỗi trục là km), một máy bay đang bay đến vị trí $A(500; 200; 10)$. Theo hành trình dự định sẽ bay đến vị trí $B(700; 200; 10)$, nhưng do thời tiết xấu nên máy bay phải chuyển hướng bay từ A đến vị trí $C(600; 300; 8)$. Hỏi máy bay đã bay chênh hướng so với dự định một góc bao nhiêu độ?

Câu 5: Chiều cao của 40 bé sơ sinh 12 ngày tuổi được chọn ngẫu nhiên ở viện nhi trung ương được nghiên cứu thống kê ở bảng dưới đây:

Tìm phương sai (làm tròn đến hàng phần chục) của 40 bé sơ sinh ở bảng thống kê trên

Câu 6: Trong không gian với hệ tọa độ $Oxyz$, cho ba điểm $A(1; 2; -1), B(2; -1; 3), C(-4; 7; 5)$. Tọa độ chân đường phân giác trong góc $B$ của tam giác $ABC$ là $(a; b; c)$. Tổng $T = a + b + c$.

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh