PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1: Cho hàm số $y = f(x)$ có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?

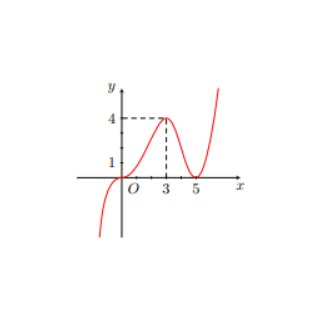
A. Hàm số đồng biến trên khoảng $(-\infty; -1)$ và $(1; +\infty)$.

B. Hàm số đồng biến trên khoảng $(0; 5)$.

C. Hàm số nghịch biến trên khoảng $(-1; 1)$.

D. Hàm số đồng biến trên khoảng $(-1; 1)$.

Câu 2: Xét hàm số $y = f(x)$ có tập xác định là $(-1; 5)$ và có bảng biến thiên như sau:

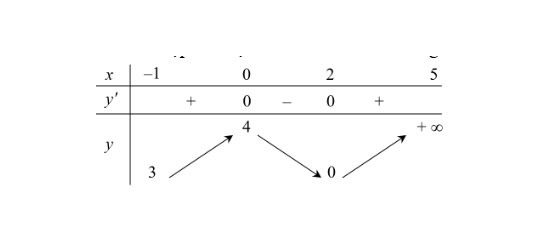
Khẳng định nào sau đây là đúng?

A. Hàm số đã cho đạt GTNN tại $x = -1$.

B. Hàm số đã cho không tồn tại GTLN.

C. Hàm số đã cho đạt GTLN tại $x = 0$.

D. Hàm số đã cho đạt GTLN tại $x = 2$.

Câu 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sqrt{5-4x}$ trên đoạn $[-1; 1]$ là:

A. $\max y = \sqrt{5}$ và $\min y = 0$.

B. $\max y = 3$ và $\min y = 1$.

C. $\max y = 0$ và $\min y = -\sqrt{5}$.

D. $\max y = 1$ và $\min y = -3$.

Câu 4: Cho hàm số $y = f(x)$ có bảng biến thiên của hàm số $f'(x)$ như hình vẽ:

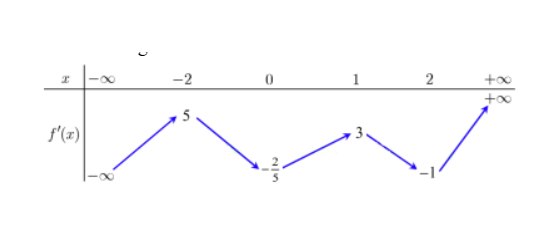
Hàm số $f(x)$ có bao nhiêu điểm cực tiểu?

A. $3$.

B. $4$.

C. $2$.

D. $5$.

Câu 5: Cho đồ thị hàm số $y = f(x)$ như hình vẽ có đường tiệm cận xiên $y = ax + b$. Khi đó, $a + b$ bằng bao nhiêu?

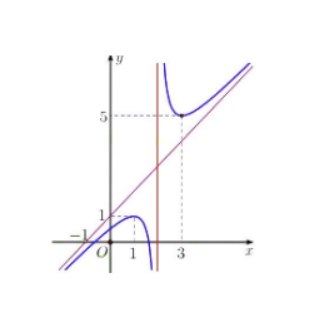
A. $1$.

B. $2$.

C. $0$.

D. $3$.

Câu 6: Cho tứ diện $ABCD$. Đặt $\overrightarrow{AB} = \vec{a}$, $\overrightarrow{AC} = \vec{b}$, $\overrightarrow{AD} = \vec{c}$. Gọi $M$ là trung điểm của đoạn $BC$. Đẳng thức nào dưới đây đúng?

A. $\overrightarrow{DM} = \frac{1}{2}(\vec{a} + \vec{b} – 2\vec{c})$.

B. $\overrightarrow{DM} = \frac{1}{2}(\vec{a} + 2\vec{b} – \vec{c})$.

C. $\overrightarrow{DM} = \frac{1}{2}(2\vec{a} + \vec{b} – \vec{c})$.

D. $\overrightarrow{DM} = \frac{1}{2}(\vec{a} – 2\vec{b} + \vec{c})$.

Câu 7: Trong không gian Oxyz, cho tam giác $ABC$ có $A(1; 0; 1), B(0; 2; 3), C(2; 1; 0)$. Độ dài đường trung tuyến $AM$ là

A. $\frac{1}{2}$.

B. $\frac{\sqrt{10}}{2}$.

C. $\frac{\sqrt{12}}{2}$.

D. $\frac{\sqrt{11}}{2}$.

Câu 8: Trong không gian Oxyz, cho $\vec{u} = \vec{i} + 3\vec{j} – 2\vec{k}$ và $\vec{v} = (2; -1; 1)$. Tính tích vô hướng $\vec{u}.\vec{v}$

A. $\vec{u}.\vec{v} = 2\sqrt{21}$.

B. $\vec{u}.\vec{v} = 2$.

C. $\vec{u}.\vec{v} = 5\sqrt{2}$.

D. $\vec{u}.\vec{v} = -3$.

Câu 9: Khi máu đi chuyển từ tim qua các động mạch chính rồi đến các mao mạch và quay trở lại qua các tĩnh mạch, huyết áp tâm thu (tức là áp lực của máu lên động mạch khi tim co bóp) liên tục giảm xuống. Giả sử một người có huyết áp tâm thu $P$ (tính bằng mmHg) được cho bởi hàm số $P(t) = \frac{25t^2 + 125}{t^2 + 1}, (0 \leq t \leq 10)$ với $t$ là thời gian được tính bằng giây. Tính tốc độ thay đổi của huyết áp sau $5$ giây kể từ khi máu rời tim.

A. Tăng $\frac{250}{169}$.

B. Tăng $\frac{375}{13}$.

C. Giảm $\frac{250}{169}$.

D. Giảm $\frac{500}{13}$.

Câu 10: Trong không gian $Oxyz$, điểm đối xứng của điểm $M(1; -2; 3)$ qua trục $Oy$ có tọa độ là

A. $(1; 0; 3)$.

B. $(-1; 0; -3)$.

C. $(-1; 2; -3)$.

D. $(-1; -2; -3)$.

Câu 11: Cho hàm số $y = f(x)$ có đồ thị như hình vẽ sau. Phát biểu nào sau đây sai?

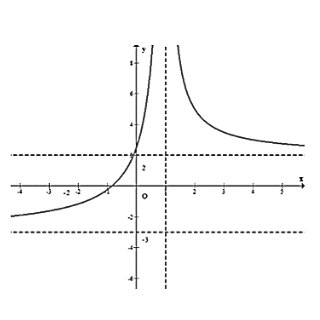
A. Đồ thị hàm số không có tiệm cận xiên.

B. $\lim_{x \to +\infty} f(x) = 2; \lim_{x \to -\infty} f(x) = -3$.

C. $\lim_{x \to 1^-} f(x) = +\infty; \lim_{x \to 1^+} f(x) = -\infty$.

D. Đồ thị hàm số có 3 đường tiệm cận.

Câu 12: Cho hàm số $y = f(x)$ có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?

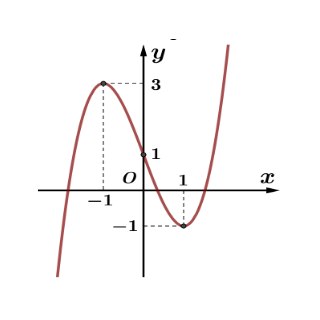
A. $y = -x^3 + 3x + 1$.

B. $y = x^3 – 3x^2 – 1$.

C. $y = x^3 – 3x + 1$.

D. $y = -x^3 + 3x + 1$.

PHẦN II. Câu trắc nghiệm đúng sai

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Hàm số $y = f(x)$ xác định, có đạo hàm trên $\mathbb{R}$ và $f'(x) = (x+1)^2(x-1)(5-x)$. Các mệnh đề sau đúng hay sai?

a) Phương trình $f'(x) = 0$ có 3 nghiệm phân biệt.

b) Hàm số $y = f(x)$ có 3 điểm cực trị.

c) $x = 5$ là điểm cực đại của hàm số $y = f(x)$.

d) $f(1) < f(-4) < f(5)$.

Câu 2: Cho hàm số $f(x) = \sin x$. Các mệnh đề sau đúng hay sai?

a) $f'(x) = \cos x$.

b) Hàm số $f(x)$ đồng biến trên khoảng $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$.

c) Hàm số $f(x)$ là hàm số chẵn.

d) Đồ thị hàm số $y = |f(x)|$ nhận $Oy$ làm trục đối xứng.

Câu 3: Một tòa nhà 6 tầng có dạng hình hộp chữ nhật với kích thước chiều dài 35m, chiều rộng 15m, chiều cao 30m. Tất cả các tầng đều cao 5m (đã tính độ dày sàn nhà của các tầng). Người ta định vị các vị trí trong tòa nhà đưa vào hệ trục tọa độ Oxyz như hình vẽ. Tòa nhà có hai cột phát wifi: vị trí $A(0; 7; 15)$, vị trí $B(35; 7; 15)$. Mỗi wifi có thể phát sóng bán kính phạm vi 25 mét. Cho biết các nhân viên: chị Hương ở tầng 1 tọa độ $(17; 0; 1)$, chị Lan ở tầng 6 tọa độ $(0; 15; 26)$, anh Ninh ở tầng 6 tọa độ $(17; 15; 26)$. Mỗi nhân viên đều sử dụng thiết bị kết nối với wifi. Mỗi kết luận sau đúng hay sai?

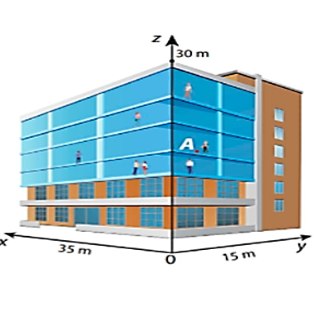
a) Tất cả ba nhân viên trên đều kết nối được với wifi ở vị trí $A$.

b) Chị Hương kết nối được với wifi của cả hai vị trí $A$ và $B$.

c) Anh Ninh không kết nối được với wifi của vị trí $B$.

d) Chị Lan không kết nối được với wifi của vị trí $B$.

Câu 4: Nhà máy đường kiểm tra khối lượng các gói đường do một máy đóng gói tự động thực hiện để kết luận máy này làm tốt hay không. Kết quả kiểm tra được biểu diễn trong bảng dưới đây:

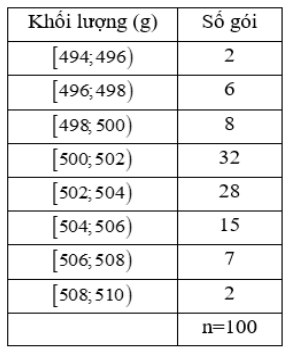
Biết rằng tiêu chuẩn mong muốn của nhà máy là khối lượng trung bình các gói đường nằm trong khoảng 500 – 504 gam và độ lệch chuẩn nhỏ hơn 3 gam thì xem như máy vận hành tốt. Mỗi kết luận sau đúng hay sai?

a) Khối lượng trung bình các gói đường của máy sản xuất có số liệu ghép nhóm trên là 502,22 gam.

b) Độ lệch chuẩn của khối lượng các gói đường làm tròn đến hàng phần mười là 3,1.

c) Sau khi kiểm tra nhà máy kết luận máy vận hành không tốt.

d) Khoảng tứ phân vị của mẫu số liệu trên đến hàng phần mười là 3,4.

PHẦN III. Câu trắc nghiệm trả lời ngắn

Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: Biết đồ thị hàm số $y = x^3 + 3x^2 – 9x – 1$ có hai cực trị $A$ và $B$. Phương trình đường thẳng $AB$ là $y = ax + b, (a, b \in \mathbb{R})$. Tính tổng $a + b$.

Câu 2: Trong không gian Oxyz cho ba điểm $A(2; 3; -1), B(3; 5; 0), C(3; 2; -3)$. Số đo góc $A$ của tam giác $ABC$ bằng bao nhiêu độ?

Câu 3: Giả sử số dân của một thị trấn sau $t$ năm kể từ năm 2000 được mô tả bởi hàm số $N(t) = \frac{20t + 15}{t + 4}, t \geq 0$, trong đó $N(t)$ được tính bằng nghìn người. Để quy hoạch đô thị, nhà quy hoạch biết rằng số dân của thị trấn không vượt quá k nghìn người. Tìm k?

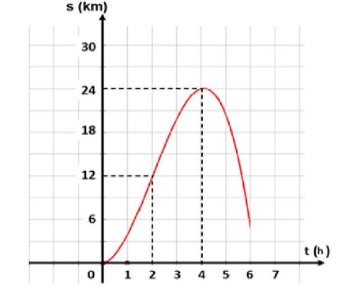
Câu 4: Bạn Tuấn tham gia giải đấu bộ năm 2024, quãng đường Tuấn đi được biểu diễn bằng hàm số $s(t) = at^3 + bt^2$ (với $a \neq 0$) có đồ thị như hình bên (trong đó $t$ là thời gian tính bằng giờ, $s$ là quãng đường tính bằng km). Khi đó, vận tốc tối đa của Tuấn đạt được là bao nhiêu km/h?

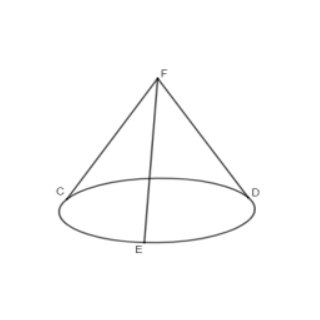
Câu 5: Một chiếc cần hình tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây (có khối lượng không đáng kể) không dãn xuất phát từ điểm $F$ và lần lượt buộc vào ba điểm $C, D, E$ cách đều nhau trên vành cần. Biết mỗi sợi dây có lực căng $2N$ và hợp với mặt cần một góc $60°$, trong lực $\vec{p}$ được xác định bởi công thức $\vec{P} = m.\vec{g}(g = 9,8m/s^2)$. Khối lượng của đĩa cần bằng bao nhiêu kilogram (làm tròn hai chữ số thập phân)?

Câu 6: Trong không gian $Oxyz$, lực không đổi $\vec{F} = 3\vec{i} + 5\vec{j} + 10\vec{k}$ làm di chuyển một vật dọc theo đoạn thẳng từ $M(1; 0; 2)$ đến $N(5; 3; 8)$. Tìm công sinh ra nếu khoảng cách được tính bằng mét và lực được tính bằng newton.

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh