Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.

Câu 1: Cho hàm số $y = f(x)$ có bảng biến thiên như sau:

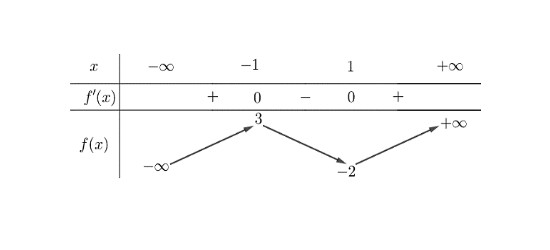
Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. $(-1; +\infty)$.

B. $(2; +\infty)$.

C. $(-1; 1)$.

D. $(-\infty; 1)$.

Câu 2: Cho hàm số $f(x)$, bảng xét dấu của $f'(x)$ như sau:

Số điểm cực trị của hàm số đã cho là

A. $0$.

B. $2$.

C. $1$.

D. $3$.

Câu 3: Cho hàm số $y = f(x)$ liên tục trên đoạn $[-1; 3]$ và có đồ thị như hình vẽ bên. Gọi $M$ và $m$ lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn $[-1; 3]$. Giá trị của $M – m$ bằng

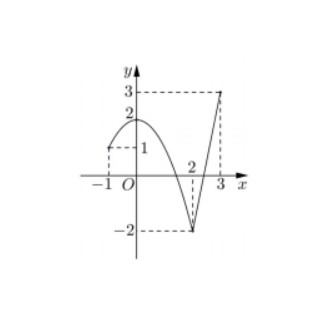
A. $1$.

B. $4$.

C. $5$.

D. $0$.

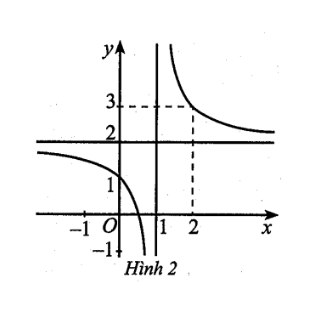
Câu 4: Đường tiệm cận xiên của đồ thị hàm số $y = \frac{x^2 + 2024}{x}$ là

A. $y = x$.

B. $y = x + 2024$.

C. $y = -x$.

D. $y = -x – 1$.

Câu 5: Cho hàm số $y = f(x)$ có $f'(x) = (e^x – 1)(x^2 – x), \forall x \in \mathbb{R}$. Số điểm cực trị của hàm số $y = f(x)$ là

A. $0$.

B. $1$.

C. $2$.

D. $3$.

Câu 6: Trong không gian, khẳng định nào là sai?

A. Hai vecto được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.

B. Nếu hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng.

C. Hai vecto $\vec{a}$ và $\vec{b}$ được gọi là bằng nhau, kí hiệu $\vec{a} = \vec{b}$, nếu chúng có cùng độ dài và cùng hướng.

D. Với mọi điểm $I$ và vecto $\vec{a}$ cho trước, có vô số điểm $M$ sao cho $\overrightarrow{IM} = \vec{a}$.

Câu 7: Cho hình lăng trụ $ABC.A’B’C’$. Đặt $\overrightarrow{AA’} = \vec{a}$, $\overrightarrow{AB} = \vec{b}$, $\overrightarrow{AC} = \vec{c}$. Hãy biểu diễn vecto $\overrightarrow{B’C}$ theo $\vec{a}, \vec{b}, \vec{c}$?

A. $\overrightarrow{B’C} = \vec{a} + \vec{b} – \vec{c}$.

B. $\overrightarrow{B’C} = -\vec{a} + \vec{b} – \vec{c}$.

C. $\overrightarrow{B’C} = \vec{a} + \vec{b} + \vec{c}$.

D. $\overrightarrow{B’C} = -\vec{a} – \vec{b} + \vec{c}$.

Câu 8: Trong không gian $Oxyz$ cho 3 điểm $A(1, 2, -1)$, $B(2, -1, 3)$, $C(-3, 5, 1)$. Tọa độ điểm $D$ sao cho tứ giác $ABCD$ là hình bình hành là

A. $(-2, 2, 5)$.

B. $(-4, 8, -5)$.

C. $(-4, 8, -3)$.

D. $(-2, 8, -3)$.

Câu 9: Trong không gian $Oxyz$, cho $\vec{a} = (1; 2; 1)$ và $\vec{b} = (-1; 3; 0)$. Vecto $\vec{c} = 2\vec{a} + \vec{b}$ có tọa độ là

A. $(1; 7; 2)$.

B. $(1; 5; 2)$.

C. $(3; 7; 2)$.

D. $(1; 7; 3)$.

Câu 10: Trong không gian $Oxyz$, hình chiếu vuông góc của điểm $A(1; 2; 5)$ trên mặt $Oxz$ có tọa độ là

A. $(0; 2; 5)$.

B. $(0; 2; 0)$.

C. $(1; 0; 5)$.

D. $(0; 0; 5)$.

Câu 11: Trong không gian $Oxyz$, cho $\vec{u} = (1; 2; 3)$, $\vec{v} = (0; -1; 1)$. Tìm tích có hướng của hai vecto $\vec{u}$ và $\vec{v}$.

A. $(5; 1; -1)$.

B. $(5; -1; -1)$.

C. $(-1; -1; -1)$.

D. $(-1; -1; 5)$.

Câu 12: Mỗi ngày bác Hương đều đi bộ để rèn luyện sức khỏe. Quãng đường đi bộ mỗi ngày (đơn vị: km) của bác Hương trong 20 ngày được thống kê lại ở bảng sau:

Phương sai của mẫu số liệu ghép nhóm là:

A. $3,39$.

B. $11,62$.

C. $0,1314$.

D. $0,36$.

Phần 2. Trắc nghiệm lựa chọn đúng sai

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Cho hàm số $y = f(x)$ liên tục và có bảng biến thiên trong đoạn $[-1; 3]$ như hình.

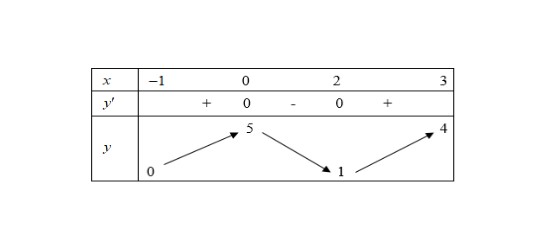
Các mệnh đề sau đúng hay sai?

a) [NB] Giá trị lớn nhất của hàm số $y = f(x)$ trên đoạn $[-1; 3]$ là $5$.

b) [TH] Tổng của giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = f(x)$ trên đoạn $[-1; 3]$ bằng $6$.

c) [TH] Hàm số $y = f(x)$ đạt giá trị nhỏ nhất trên đoạn $[0; 1]$ khi $x = 0$.

d) [VD,VDC] Hàm số $g(x) = f(4-x)$ có $g(3) < 4$ đạt giá trị nhỏ nhất và giá trị lớn nhất trên đoạn $[1; 3]$ bằng $a, b$. Khi đó giá trị của $a^2 + b^2 = 13$.

Câu 2: Ở một sân bay, vị trí của máy bay được xác định bởi điểm $M$ trong không gian $Oxyz$ như hình vẽ.

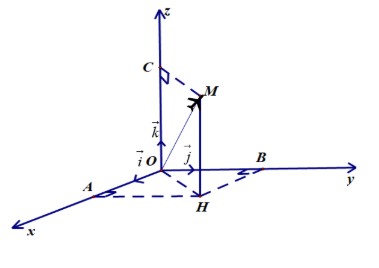
Gọi $H$ là hình chiếu vuông góc của $M$ xuống mặt phẳng $(Oxy)$. Cho biết $OM = 50$, $\widehat{(I,\overrightarrow{OH})} = 64°$, $\widehat{(\overrightarrow{OH},\overrightarrow{OM})} = 48°$. Các mệnh đề sau đúng hay sai?

a) [NB] $OH = OM.\cos HOM = 50.\cos 48°$.

b) [TH] $OC = OM.\sin HOM$.

c) [TH] $AH = OH.\cos AOH$.

d) [VD, VDC] Tọa độ của điểm $M$ là $(14,7; 30,1; 37,2)$.

Câu 3: Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A(-2; 3; 1)$ và $B(5; 6; 2)$.

a) [NB] $\overrightarrow{AB} = (7; 3; 1)$.

b) [TH] Hình chiếu của $B(5; 6; 2)$ trên mặt phẳng $(Oxz)$ là $B'(0; 6; 0)$.

c) [TH] Có đúng một điểm $I$ thuộc trục $Ox$ sao cho $\triangle IAB$ là tam giác vuông tại $I$.

d) [VD] Đường thẳng $AB$ cắt mặt phẳng $(Oxz)$ tại điểm $M$ khi đó $\frac{AM}{BM} = \frac{3}{7}$.

Câu 4: Một nông trường nghiên cứu sự phát triển của cây keo 3 năm tuổi tại hai khu vườn $A$ và $B$. Ở khu vườn $A$ kết quả đo chiều cao của các cây keo được cho ở bảng sau:

Ở khu vườn $B$ từ mẫu số liệu về chiều cao của cây keo 3 năm tuổi người ta tính được khoảng tứ phân vị là 0,5. Các mệnh đề sau đúng hay sai?

a)[NB] Cỡ của mẫu số liệu trong bảng trên là $100$.

b)[TH] Tứ phân vị thứ nhất (làm tròn đến hàng phần trăm) của mẫu số liệu ghép nhóm trong bảng trên là: $Q_1 = 8,87$.

c)[TH] Khoảng tứ phân vị (làm tròn đến hàng phần trăm) của mẫu số liệu ghép nhóm trong bảng trên là: $\Delta Q = 0,30$.

d) [VD] Chiều cao của các cây vườn $A$ đồng đều hơn vườn $B$.

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn

Thí sinh trả lời từ câu 1 đến câu 6

Câu 1: Một sợi dây có chiều dài là $6(m)$, được chia thành hai phần. Phần thứ nhất được uốn thành hình tam giác đều, phần thứ hai uốn thành hình vuông. Hỏi độ dài của cạnh hình tam giác đều bằng bao nhiêu để diện tích hai hình thu được là nhỏ nhất? (Làm tròn kết quả đến hai chữ số thập phân).

Câu 2: Tìm số đường tiệm cận của đồ thị hàm số sau: $y = \frac{-2x-1}{\sqrt{x^2+x+2}}$.

Câu 3: Cho hàm số $y = f(x)$ liên tục trên $\mathbb{R}$ và có đạo hàm $f'(x) = (x+1)^2(x-1)^3(2-x)$. Hàm số $y = f(x)$ đồng biến trên khoảng $(a;b)$. Tính $\frac{a}{b}$.

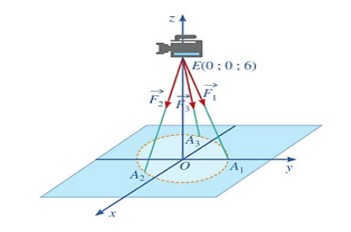
Câu 4: Một chiếc máy được đặt trên một giá đỡ ba chân với điểm đặt $F(0;0;6)$ và các điểm tiếp xúc với mặt đất của ba chân lần lượt là $A_1(0;1;0), A_2\left(\frac{\sqrt{3}}{2},-\frac{1}{2};0\right), A_3\left(-\frac{\sqrt{3}}{2},-\frac{1}{2};0\right)$. Biết rằng trọng lực tổng hợp của chiếc máy là $300N$. Tìm được tọa độ của các lực tác dụng lên giá đỡ $\overrightarrow{F_1}, \overrightarrow{F_2}, \overrightarrow{F_3}$ khi đó tích vô hướng của $\overrightarrow{F_1}.\overrightarrow{F_2}$ bằng? (làm tròn kết quả đến hàng đơn vị)

Câu 5: Cho hình chóp $S.ABC$ có $SA = SB = SC = AB = AC = a$ và $BC = a\sqrt{2}$. Tính cos góc của hai vecto $\overrightarrow{SC}$ và $\overrightarrow{AB}$.

Câu 6: Kết quả điều tra về số giờ làm thêm trong một tuần của 100 sinh viên được cho ở biểu đồ bên

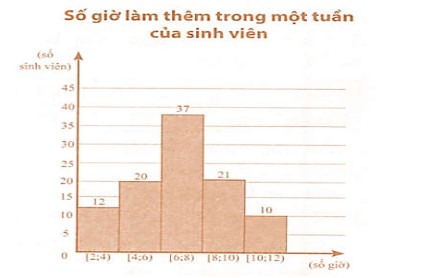
Tìm khoảng tứ phân vị của mẫu số liệu trên (làm tròn kết quả đến hàng phần trăm).

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh