PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1: Tìm giá trị nhỏ nhất m của hàm số $y = \frac{4-6x}{x-4}$ trên đoạn $[-4; 3]$.

A. $m = -\frac{13}{2}$.

B. $m = 18$.

C. $m = 14$.

D. $m = -\frac{7}{2}$.

Câu 2: Tìm giá trị lớn nhất M của hàm số $y = -x^3 + 6x^2 + 1$ trên đoạn $[-1; 5]$.

A. $M = 33$.

B. $M = 33$.

C. $M = 1$.

D. $M = 1$.

Câu 3: Đồ thị như hình vẽ dưới đây là của hàm số nào?

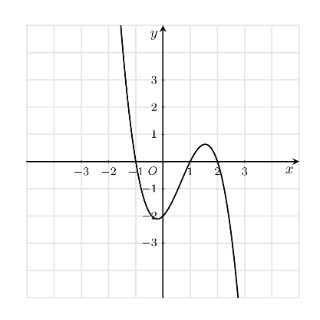
A. $y = -x^3 + 2x^2 + x + 2$.

B. $y = -x^3 – 2x^2 – 2$.

C. $y = -x^3 + 2x^2 + x – 2$.

D. $y = x^3 + 2x^2 + x – 2$.

Câu 4: Bảng biến thiên như hình vẽ dưới đây là của hàm số nào?

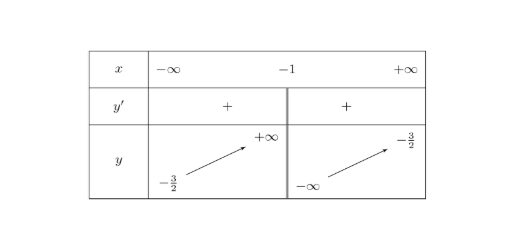
A. $y = \frac{-3x-4}{-2x-2}$.

B. $y = \frac{3x-4}{2x-2}$.

C. $y = \frac{-3x+4}{-2x-2}$.

D. $y = \frac{3x-2}{5-2x}$.

Câu 5: Tiệm cận đứng của đồ thị trong hình vẽ sau là:

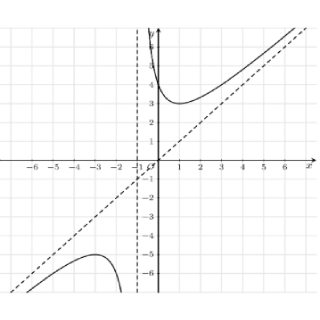
A. $x = 1$.

B. $x = -1$.

C. $y = 1$.

D. $y = -1$.

Câu 6: Cho hàm số $y = f(x)$ xác định với mọi $x \in \mathbb{R}$ có bảng biến thiên như hình vẽ dưới đây. Hàm số nghịch biến trên khoảng nào trong các khoảng sau?

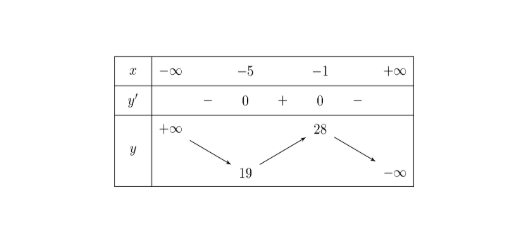
A. $(-\infty; -1)$

B. $(9; +\infty)$

C. $(-3; 12)$

D. $(-\infty; 9)$

Câu 7: Cho hàm số $y = f(x)$ có đạo hàm trên $\mathbb{R}$ thỏa mãn $f'(x) > 0, \forall x \in (-1; 1)$ và $f'(x) < 0, \forall x \in (1; 3)$. Phát biểu nào sau đây là đúng?

A. Hàm số $y = f(x)$ đồng biến trên cả hai khoảng $(-1; 1)$ và $(1; 3)$.

B. Hàm số $y = f(x)$ nghịch biến trên cả hai khoảng $(-1; 1)$ và $(1; 3)$.

C. Hàm số $y = f(x)$ đồng biến trên khoảng $(-1; 1)$ và nghịch biến trên khoảng $(1; 3)$.

D. Hàm số $y = f(x)$ nghịch biến trên khoảng $(-1; 1)$ và đồng biến trên khoảng $(1; 3)$.

Câu 8: Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $O$. Phát biểu nào sau đây là sai?

A. $\overrightarrow{OA} – \overrightarrow{OB} = \overrightarrow{AB}$.

B. $\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} = \vec{0}$.

C. $\overrightarrow{AB} + \overrightarrow{CD} = \vec{0}$.

D. $\overrightarrow{SA} + \overrightarrow{SB} + \overrightarrow{SC} + \overrightarrow{SD} = 4\overrightarrow{SO}$.

Câu 9: Trong không gian $Oxyz$, cho hai điểm $M(2; -3; 5)$ và $N(-2; 7; 11)$. Tọa độ trung điểm $H$ của đoạn $MN$ là:

A. $H(0; 2; 8)$.

B. $H(0; 4; 16)$.

C. $H(-4; 10; 6)$.

D. $H(4; -10; -6)$.

Câu 10: Trong không gian $Oxyz$ cho hai vecto $\vec{u} = (4; 3; 6), \vec{v} = (1; -2; 5)$.

Tích vô hướng của hai vecto $\vec{u}.\vec{v}$ bằng:

A. $\vec{u}.\vec{v} = 28$.

B. $\vec{u}.\vec{v} = 30$.

C. $\vec{u}.\vec{v} = 39$.

D. $\vec{u}.\vec{v} = 40$.

Câu 11: Bảng sau (bảng 1) thống kê cân nặng của 50 quả cam được lựa chọn ngẫu nhiên sau khi thu hoạch ở một nông trường. Khoảng tứ phân vị của mẫu số liệu ghép nhóm đó là (làm tròn đến hàng phần chục):

A. $68,7$.

B. $68,8$.

C. $69$.

D. $68,9$.

Câu 12: Xét mẫu số liệu ghép nhóm được cho ở Bảng 1 trang câu 11. Độ lệch chuẩn của mẫu số liệu ghép nhóm đó là (làm tròn đến hàng phần trăm):

A. $39$.

B. $39,1$.

C. $39,2$.

D. $39,3$.

PHẦN II. Câu trắc nghiệm đúng sai

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Cho hàm số $y = f(x)$ xác định trên $\mathbb{R}$ và có bảng biến thiên như hình vẽ. Xét tính đúng sai của các khẳng định sau?

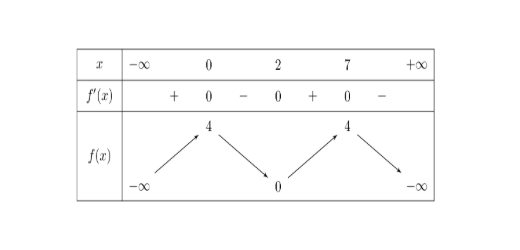
a) Hàm số đồng biến trên khoảng $(0; 7)$

b) Hàm số nghịch biến trên khoảng $(7; +\infty)$.

c) $f(9) > f(7)$.

d) Phương trình $f'(4x + 5) = 0$ nhận $x = -\frac{5}{4}$ làm nghiệm.

Câu 2: Cho hàm số $y = \frac{-x^2 – 3x – 1}{x + 3}$. Xét tính đúng-sai của các khẳng định sau.

a) Tập xác định của hàm số là $\mathbb{R} \setminus {-3}$.

b) Hàm số có đạo hàm là $y’ = \frac{-x^2 – 6x – 8}{(x + 3)^2}$.

c) Tiệm cận xiên của đồ thị hàm số là đường thẳng: $y = -x$

d) Điểm cực tiểu của hàm số là $x = -2$.

Câu 3: Bảng sau biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của một công ty (đơn vị triệu đồng).

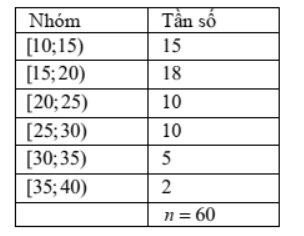
Các mệnh đề sau đúng hay sai?

a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là 30

b) Tứ phân vị thứ ba là: $Q_3 = 26$.

c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là: $\Delta_Q = 11$.

d) Mức lương 39tr là giá trị ngoại lệ của mẫu số liệu trên.

Câu 4: Trong một hội phòng khách chính với chiều dài 8m, rộng 6m và cao 4m có 3 cây quạt. Cây quạt A treo cách bức tường bên trái (có cửa sổ) 2 m và cách trần 1 m, cây quạt B treo chính giữa bức tường dài 6 m và cách trần 1.5 m, cây quạt C gần ngay tâm của trần căn phòng. Chọn hệ trục tọa độ như hình vẽ sau (đơn vị: mét)

a) Tọa độ cây quạt A là $A(0; 2; 3)$.

b) Tọa độ cây quạt B là $B\left(0; 3; \frac{5}{2}\right)$.

c) Tọa độ cây quạt C là $C(3; 4; 4)$

d) Trong 3 cây quạt trên khoảng cách giữa hai cây quạt A và B là lớn nhất.

PHẦN III. Câu trắc nghiệm trả lời ngắn

Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: Giá sử hàm số $f(x) = 2x^3 – 9x^2 + 12x + 5$ đạt cực đại tại $x = m$ và đạt cực tiểu tại $x = n$. Giá trị của biểu thức $A = 3m + 2n$ là bao nhiêu?

Câu 2: Sự phân hủy của rác thải hữu cơ có trong nước sẽ làm tiêu hao oxygen hòa tan trong nước. Nồng độ oxygen (mg/l) trong một hồ nước sau t giờ $(t \geq 0)$ khi một lượng rác thải hữu cơ bị xả vào hồ được xấp xỉ bởi hàm số (với đồ thị của hàm số $y(t)$ có dạng như một đường cong).

$y = y(t) = 10 – \frac{20t}{4t^2 + 1}$.

Vào thời điểm nào nồng độ oxygen trong nước thấp nhất?

Câu 3: Một công ty vận tải có chi phí trung bình (tính bằng nghìn đồng) cho việc vận chuyển $t$ tấn hàng hóa trong một ngày được cho bởi công thức: $f(t) = \frac{80t + 1600}{t}$. Xem $y = f(t)$ là một hàm số xác định trên nửa khoảng $[0; +\infty)$. Đồ thị hàm số $y = f(t)$ có đường tiệm cận ngang là $y = a$. Giá trị của $a$ là bao nhiêu?

Câu 4: Một camera wifi mini trong hình bên trái được biểu diễn trong không gian Oxyz như hình bên phải. Vectơ $\overrightarrow{AB}$ có tọa độ là $(a; b; c)$. Giá trị của $T = a + b + c$ bằng bao nhiêu?

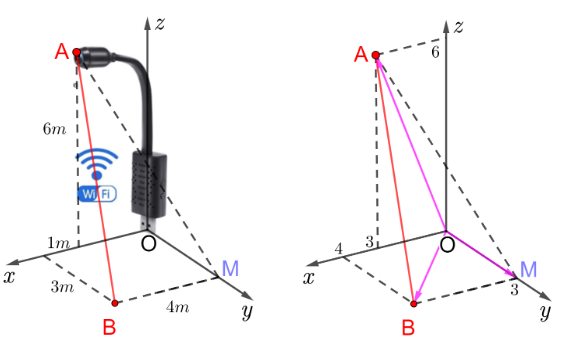
Câu 5: Trong 15 giây đầu tiên, một chất điểm chuyển động theo phương trình $s(t) = 2t^3 – 15t^2 + 24t + 5$, trong đó $t$ tính bằng giây và $s$ tính bằng mét. Chất điểm có gia tốc tức thời lớn nhất bằng bao nhiêu mét trên giây bình phương trong 15 giây đầu tiên đó?

Câu 6: Một trung tâm dự báo thời tiết khám hai drone trong một buổi phun thuốc phòng trừ sâu bệnh trên cánh đồng lúa (hình bên dưới). Drone I ở vị trí $A$ cách vị trí điều khiển $80m$ về phía nam và cách mặt đất $10m$.

Drone II ở vị trí $B$ cách vị trí điều khiển $50m$ về phía đông và cách mặt đất $5m$. Chọn hệ trục tọa độ $Oxyz$ với gốc $O$ là vị trí người điều khiển, mặt phẳng $(Oxy)$ trùng với mặt đất, trục $Ox$ có hướng trung với hướng nam, trục $Oy$ trùng với hướng đông, trục $Oz$ vuông góc với mặt đất hướng lên phía trời, đơn vị trên mỗi trục tính theo mét. Khoảng cách giữa hai drone đó bằng bao nhiêu mét (làm tròn đến hàng đơn vị)?

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh