Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Cho hàm số $y = f(x)$ có bảng biến thiên như sau:
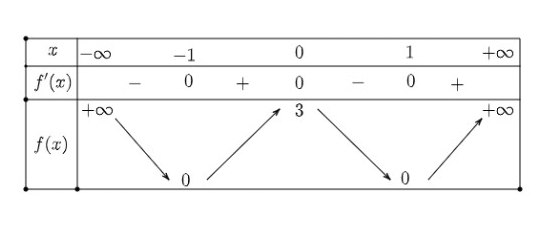
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. $(1; +\infty)$.
B. $(0; 1)$.
C. $(-1; 0)$.
D. $(0; +\infty)$.
Câu 2: Cho hàm số $y = f(x)$ có đồ thị như hình bên.
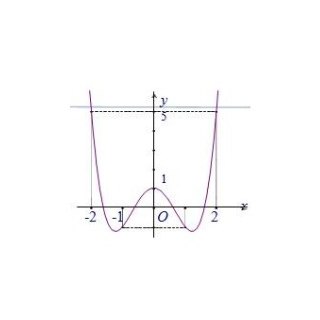
Tìm giá trị lớn nhất của hàm số $y = f(x)$ trên đoạn $[-1; 2]$.
A. $1$.
B. $2$.
C. $5$.
D. $0$.
Câu 3: Cho hàm số $y = f(x)$ có đồ thị như hình vẽ.
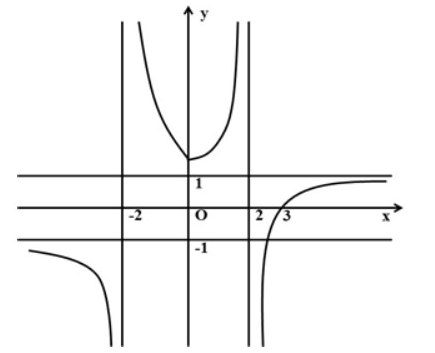
Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
A. $4$.
B. $2$.
C. $1$.
D. $3$.
Câu 4: Đường cong trong hình là đồ thị của hàm số nào dưới đây?
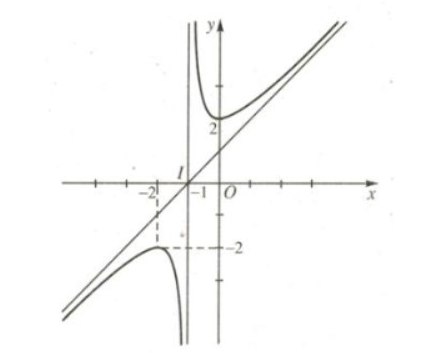
A. $y = \frac{x^2 – 2x – 3}{x – 2}$.
B. $y = \frac{x^2 – 2x}{x + 1}$.
C. $y = \frac{x^2 + 3x}{x – 2}$.
D. $y = \frac{x^2 + 2x + 2}{x + 1}$.
Câu 5: Bảng biến thiên trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
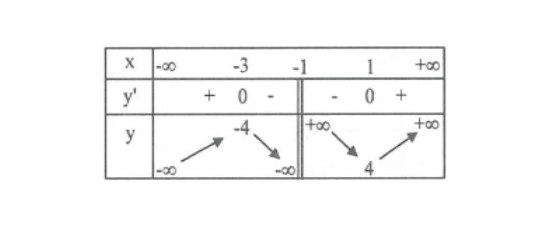
A. $y = \frac{x^2 – 2x}{x + 1}$.
B. $y = \frac{x^2 + 3x}{x + 1}$.
C. $y = \frac{1 – x^2}{x}$.
D. $y = \frac{x^2 + 2x + 5}{x + 1}$.
Câu 6: Trong không gian với hệ trục tọa độ $Oxyz$, cho hai điểm $A(1; 2; -1), B = (1; 3; 1)$ thì tọa độ của điểm $B$ là:
A. $B(2; 5; 0)$.
B. $B(0; -1; -2)$.
C. $B(0; 1; 2)$.
D. $B(-2; -5; 0)$.
Câu 7: Trong không gian với hệ trục tọa độ $Oxyz$, cho $\vec{a} = (2; -3; 3)$, $\vec{b} = (0; 2; -1)$, $\vec{c} = (3; -1; 5)$. Tìm tọa độ của vectơ $\vec{u} = 2\vec{a} + 3\vec{b} – 2\vec{c}$.
A. $(10; -2; 13)$.
B. $(-2; 2; -7)$.
C. $(-2; -2; 7)$.
D. $(-2; 2; 7)$.
Câu 8: Trong không gian với hệ tọa độ $Oxyz$, cho các vectơ $\vec{a} = (2; m – 1; 3)$, $\vec{b} = (1; 3; -2n)$. Tìm $m$, $n$ để các vectơ $\vec{a}$, $\vec{b}$ cùng phương.
A. $m = 7; n = -\frac{3}{4}$.
B. $m = 7; n = -\frac{4}{3}$.
C. $m = 4; n = -3$.
D. $m = 1; n = 0$.
Câu 9: Các ô tô đi trên một con đường có biển báo giới hạn tốc độ là 55 dặm một giờ được kiểm tra tốc độ bởi một hệ thống ra đa cảnh sát. Bảng phân phối tần số về tốc độ được cho bởi bảng sau:

Tìm khoảng tứ phân vị của mẫu số liệu trên.
A. $\Delta_Q \approx 7,172$.
B. $\Delta_Q = 16$.
C. $\Delta_Q = 13,5$.
D. $\Delta_Q = 35$.
Câu 10: Thu nhập gia định/năm của hai nhóm dân cư ở hai xã của một huyện được cho trong bảng sau: (đv: triệu đồng)
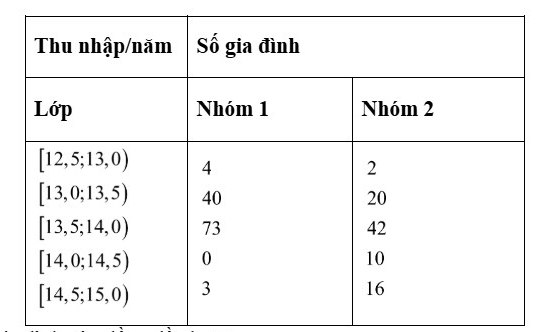
Thu nhập của nhóm gia định nào đồng đều hơn?
A. Nhóm 1.
B. Nhóm 2.
C. Cả hai nhóm.
D. Không thể xác định được nhóm nào đồng đều hơn.
Câu 11: Để chuẩn bị may đồng phục cho học sinh, người ta đo chiều cao của 36 học sinh trong một lớp học và thu được các số liệu thống kê ghép nhóm được trình bày trong bảng dưới đây.
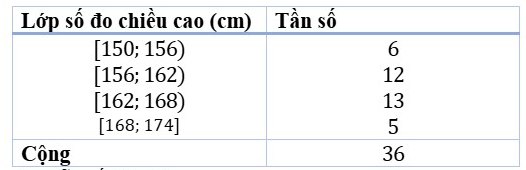
Tìm khoảng biến thiên của mẫu số liệu trên.
A. $R = 25$.
B. $R = 24$.
C. $R = 10$.
D. $R = 36$.
Câu 12: Để chuẩn bị may đồng phục cho học sinh, người ta đo chiều cao của 36 học sinh trong một lớp học và thu được các số liệu thống kê ghép nhóm được trình bày trong bảng dưới đây.
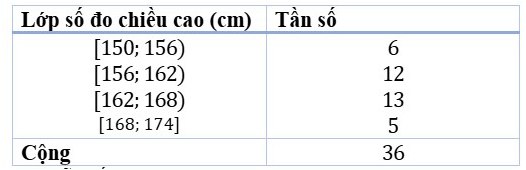
Tìm khoảng tứ phân vị của mẫu số liệu trên
A. $\Delta_Q = 36$.
B. $\Delta_Q = 9$.
C. $\Delta_Q \approx 8,65$.
D. $\Delta_Q = 5$.
PHẦN II. Câu trắc nghiệm đúng sai
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho hàm số $y = f(x)$ có đồ thị như hình vẽ bên.
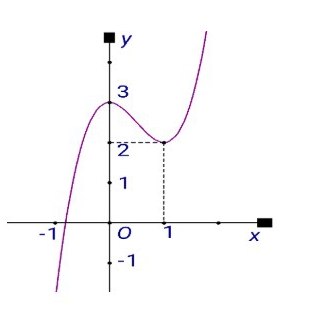
a) Hàm số nghịch biến trên khoảng $(0; 1)$
b) Hàm số đạt cực trị tại các điểm $x = 0$ và $x = 1$
c) Hàm số đồng biến trên khoảng $(-\infty; 0)$ và $(1; +\infty)$
d) Hàm số đồng biến trên khoảng $(-\infty; 3)$ và $(1; +\infty)$
Câu 2: Cho hàm số $y = f(x)$ liên tục trên các khoảng xác định và có bảng biến thiên như hình vẽ sau:
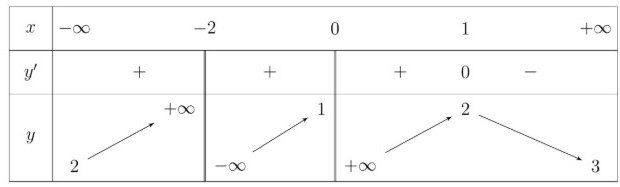
a) Số đường tiệm cận đứng của đồ thị hàm số đã cho là 2
b) Đồ thị hàm số $y = f(x)$ có ba đường tiệm cận ngang $y = 1; y = 2; y = 3$
c) Hàm số $y = f(x)$ nghịch biến trong khoảng $(1; +\infty)$
d) Hàm số $y = f(x)$ có hai điểm cực trị.
Câu 3: Trong không gian $Oxyz$, cho hình bình hành $ABCD$. Biết $A(-1; 1; 2), B(1; 0; 3), C(0; 2; -2)$.
a) Tọa độ vectơ $\overrightarrow{BC} = (-1; 2; -5)$.
b) Tọa độ vectơ $\overrightarrow{AB} = 2\vec{i} – \vec{j} + \vec{k}$.
c) Tọa độ điểm $D$ là $D(-2; 3; -3)$.
d) Tọa độ vectơ $\overrightarrow{AD} = -\vec{i} + 2\vec{j} + 5\vec{k}$.
Câu 4: Điều tra cân nặng của các học sinh lớp 11D cho trong bảng sau:

a) Mẫu số liệu trên có khoảng biến thiên là 30.
b) Mẫu số liệu trên có $Q_1 \approx 40,1; Q_3 \approx 50,39$.
c) Khoảng tứ phân vị là $\Delta_Q = 7$.
d) Mẫu số liệu trên có trung vị là 51,75.
PHẦN III. Câu trắc nghiệm trả lời ngắn
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Cho hàm số $y = f(x)$ có đạo hàm liên tục trên $\mathbb{R}$. Hàm số $y = f'(x)$ có đồ thị như hình vẽ bên dưới:
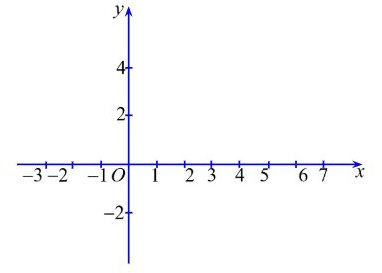
Hàm số $y = f(x)$ có mấy cực tiểu?
Câu 2: Bạn Hiền là một học sinh lớp 12, bố bạn là một thợ hàn. Bố bạn định làm một chiếc thùng hình trụ từ một mảnh tôn có chu vi 120 cm theo cách dưới đây:
Bằng kiến thức đã học em giúp bố bạn Hiền chọn mảnh tôn để làm được chiếc thùng có thể tích lớn nhất, khi đó chiều dài, rộng của mảnh tôn lần lượt là bao nhiêu?
Câu 3: Số dân của một thị trấn sau $t$ năm kể từ năm 1970 được ước tính bởi công thức $f(t) = \frac{26t + 10}{t + 5}$ ($f(t)$ được tính bằng nghìn người) (Nguồn: Giải tích 12 nâng cao, NXBGD Việt Nam, 2020). Xem $y = f(t)$ là một hàm số xác định trên nửa khoảng $[0; +\infty)$. Đồ thị hàm số $y = f(t)$ có đường tiệm cận ngang là $y = a$. Giá trị của $a$ là bao nhiêu?
Câu 4: Cho tứ diện $ABCD$ có $AB, AC, AD$ đôi một vuông góc với nhau và $AD = 2, AB = AC = 1$. Gọi $I$ là trung điểm của đoạn thẳng $BC$ và $G$ là trọng tâm của tam giác $ABD$. Tính độ dài $BI$.
Câu 5: Trong không gian với hệ tọa độ $Oxyz$ cho hai điểm $A(4; 2; 1)$, $B(-2; -1; 4)$. Tìm tọa độ điểm $M$ thỏa mãn đẳng thức $\overrightarrow{AM} = 2\overrightarrow{MB}$.
Câu 6: Chiều dài của 60 lá đường xi trường thành được mô tả trong bảng sau:
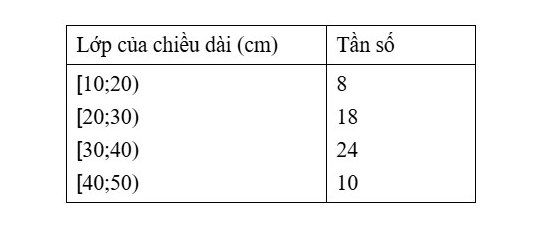
Khoảng tứ phân vị của mẫu số liệu trên là:

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh

