PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.

Câu 1: Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là đúng?

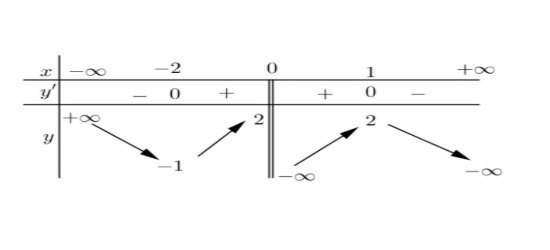
A. Hàm số không có giá trị cực tiểu.

B. Hàm số đạt cực đại tại $x = 2$.

C. Giá trị cực đại của hàm số bằng $1$.

D. Hàm số đạt cực tiểu tại $x = -2$.

Câu 2: Cho hàm số $y = f(x)$ liên tục trên $[-3; 2]$ và có bảng biến thiên như sau

Gọi $M, m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f(x)$ trên $[-3; 2]$. Giá trị $M + m$ bằng:

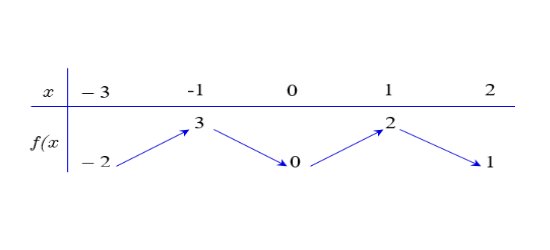
A. $4$.

B. $3$.

C. $1$.

D. $2$.

Câu 3: Hình vẽ bên là đồ thị của hàm số nào sau đây?

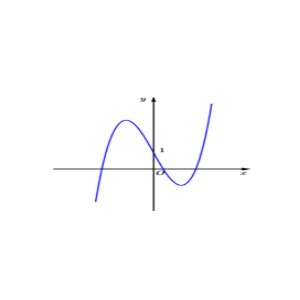
A. $y = -x^3 + x – 1$.

B. $y = -x^3 – 3x + 1$.

C. $y = x^4 – x^2 + 1$.

D. $y = x^3 – 3x + 1$.

Câu 4: Cho hình hộp $ABCD.A’B’C’D’$ (xem hình dưới), tổng của $\overrightarrow{DA} + \overrightarrow{DC} + \overrightarrow{DD’}$ là vectơ nào dưới đây?

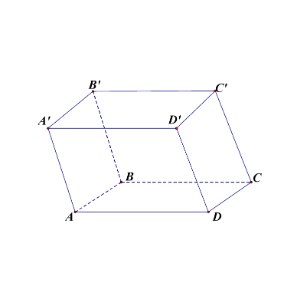
A. $\overrightarrow{DB’}$.

B. $\overrightarrow{DB}$.

C. $\overrightarrow{BD}$.

D. $\overrightarrow{BD’}$.

Câu 5: Trong không gian $Oxyz$, cho hai điểm $A(1; 1; -2)$ và $B(2; 2; 1)$. Vectơ $\overrightarrow{AB}$ có tọa độ là:

A. $(3; 3; -1)$.

B. $(-1; -1; -3)$.

C. $(3; 1; 1)$.

D. $(1; 1; 3)$.

Câu 6: Trong không gian với hệ trục tọa độ $Oxyz$ cho ba điểm $A(1; 3; 4)$; $B(1; 0; -2)$ và $C(4; 0; 1)$.

Tọa độ trọng tâm $G$ của tam giác $ABC$ là:

A. $G(3; 0; 2)$.

B. $G(2; 1; 1)$.

C. $G(1; 1; 3)$.

D. $G(3; 0; -1)$.

Câu 7: Tính $\int(e^x + e^{-2x})dx$ có kết quả bằng:

A. $e^x – 2e^{-2x} + C$.

B. $e^x + e^{-2x} + C$.

C. $e^x – \frac{1}{2}e^{-2x} + C$.

D. $\frac{e^{x+1} + e^{-2x+1}}{x+1} + \frac{1}{-2x+1} + C$.

Câu 8: Diện tích hình phẳng giới hạn bởi hai đường thẳng $x = 0, x = \pi$, đồ thị hàm số $y = \cos x$ và trục $Ox$ là:

A. $S = \int_0^\pi \cos x dx$.

B. $S = \int_0^\pi \cos^2 x dx$.

C. $S = \int_0^\pi |\cos x| dx$.

D. $S = \pi \int_0^\pi |\cos x| dx$.

Câu 9: Trong không gian $Oxyz$, cho điểm $A(4; 2; -3)$. Hình chiếu vuông góc của điểm $A$ trên mặt phẳng $(Oxy)$ có tọa độ là:

A. $(0; 2; -3)$.

B. $(4; 2; -3)$.

C. $(0; 0; -3)$.

D. $(4; 2; 0)$.

Câu 10: Hàm số $F(x) = 2x^3 – 2x + 1$ là một nguyên hàm của hàm số nào sau đây?

A. $f(x) = 6x^2 – 2$.

B. $f(x) = \frac{1}{2}x^4 – x^2 + x$.

C. $f(x) = \frac{1}{2}x^4 – x^2 + x + C$.

D. $f(x) = 6x^2 – 2 + C$.

Câu 11: Cho hàm số $y = f(x)$ có bảng biến thiên như sau:

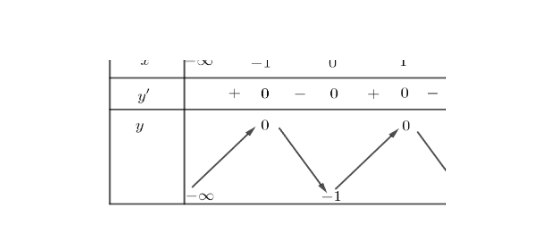
Hàm số đã cho đồng biến trên khoảng nào sau đây?

A. $(0; 1)$.

B. $(-\infty; 1)$.

C. $(1; +\infty)$.

D. $(-1; 0)$.

Câu 12: Tìm đường tiệm cận đứng của đồ thị hàm số $y = \frac{3-2x}{x-2}$?

A. $x = -2$.

B. $x = 2$.

C. $y = -2$.

D. $y = 3$.

PHẦN II. Câu trắc nghiệm đúng sai

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S).

Câu 1: Cho hàm số $y = f(x) = \frac{-x^2 + 2x – 1}{x + 2}$ (C).

a) Hàm số đồng biến trên khoảng $(-5; 1)$.

b) Đồ thị hàm số có điểm cực tiểu là $(-5; 12)$.

c) Đồ thị hàm số có 1 đường tiệm cận xiên có dạng $y = ax + b$ trong đó $a > b$.

d) Gọi $M$ là điểm bất kì thuộc đồ thị (C). Tích khoảng cách từ điểm $M$ đến hai tiệm cận của đồ thị (C) bằng $\frac{9\sqrt{2}}{2}$.

Câu 2: Xét một chất điểm chuyển động dọc theo trục $Ox$. Tọa độ của chất điểm tại thời điểm $t$ được xác định bởi hàm số $x(t) = t^3 – 6t^2 + 9t$ với $t > 0$. Khi đó $x'(t)$ là vận tốc của chất điểm tại thời điểm $t$, kí hiệu $v(t) \cdot v'(t)$ là gia tốc chuyển động của chất điểm tại thời điểm $t$, kí hiệu $a(t)$.

Các mệnh đề sau đúng hay sai?

a) Hàm $v(t) = 3t^2 – 12t + 9$

b) Hàm $a(t) = 6t – 12$

c) Trong khoảng từ $t = 0$ đến $t = 2$ thì vận tốc của chất điểm tăng

d) Từ $t = 2$ trở đi thì vận tốc của chất điểm giảm

Câu 3: Trong không gian $Oxyz$, cho hình bình hành $ABCD$, biết $A(-1; 0; 3), B(2; 1; -1), C(3; 2; 2)$.

a) Tọa độ của điểm $D$ là $D(0; 1; 6)$.

b) Điểm $M \in (Oxy)$ sao cho $A, M, B$ thẳng hàng có tọa độ $M\left(\frac{5}{4}; -\frac{3}{4}; 0\right)$.

c) Tọa độ điểm $N$ thỏa mãn $\overrightarrow{NA} + \overrightarrow{NB} – 3\overrightarrow{NC} = \vec{0}$ là $N(10; 5; 4)$.

d) Cosin góc $C$ của tam giác $ABC$ bằng $\frac{\sqrt{231}}{77}$.

Câu 4: Cho hàm số $F(x) = 4x^3 + 3x$ là một nguyên hàm của hàm số $f(x)$.

a) $\int f(x)dx = F(x) + C$.

b) $f(x) = x^4 + \frac{3x^2}{2} + C$.

c) Nếu $G(x)$ cũng là một nguyên hàm của $f(x)$ và $G(1) = 2$ thì $G(x) = F(x) + 5$

d) $\int_1^2 f(x)dx = 7$.

PHẦN III. Câu trắc nghiệm trả lời ngắn

Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: Biết hàm số $y = \frac{x^2 + 2x + 2}{x + 1}$ nghịch biến trên khoảng $(a; -1)$ và $(b; 0)$. Tính $\frac{a + 1}{2} + b$.

Câu 2: Cho tứ diện $ABCD$ có $AC$ và $BD$ cùng vuông góc với $AB$. Gọi $M, N$ lần lượt là trung điểm của hai cạnh $AB, CD$. Giá trị $k$ bằng bao nhiêu để $\overrightarrow{MN} = k(\overrightarrow{AC} + \overrightarrow{BD})$

Câu 3: Cho $\int_{-1}^3 f(x) = 12$, $F(x)$ là một nguyên hàm của $f(x)$ trên $[-1; 3]$ và $F(-1) = \frac{7}{2}$. Tính $F(3)$

Câu 4: Một hộp sữa dung tích $1$ lít có dạng hình hộp chữ nhật với đáy là hình vuông cạnh $x(cm)$ và chiều cao $h(cm)$. Tìm giá trị của $x(cm)$ để diện tích toàn phần của hình hộp là nhỏ nhất.

Câu 5: Hai chiếc khinh khí cầu bay lên từ cùng một địa điểm. Chiếc thứ nhất nằm cách điểm xuất phát $2 km$ về phía nam và $1 km$ về phía đông, đồng thời cách mặt đất $0,5 km$. Chiếc thứ hai nằm cách điểm xuất phát $1 km$ về phía bắc và $1,5 km$ về phía tây, đồng thời cách mặt đất $0,8 km$.

Chọn hệ trục tọa độ $Oxyz$ với gốc $O$ đặt tại điểm xuất phát của hai khinh khí cầu, mặt phẳng $(Oxy)$ trùng với mặt đất với trục $Ox$ hướng về phía nam, trục $Oy$ hướng về phía đông và trục $Oz$ hướng thẳng đứng lên trời như hình vẽ), đơn vị đo lấy theo kilômét.

Xác định khoảng cách giữa hai khinh khí cầu (làm tròn kết quả đến chữ số thập phân thứ hai).

Câu 6: Ở một bể chứa nước có chứa $1000$ lít nước ngọt. Người ta bơm nước biển có nồng độ muối là $30$ gam/lít vào bể nước với tốc độ là $25$ lít/phút. Để biết nồng độ muối của nước trong bể

sau $t$ phút kể từ khi bắt đầu bơm, người ta sẽ lấy khối lượng muối bơm vào sau $t$ phút chia cho tổng dung tích bể sau thời điểm $t$ phút. Như vậy hàm số biểu thị nồng độ muối của nước trong bể sau $t$ phút kể từ khi bắt đầu bơm có dạng $C(t) = \frac{at}{b + t}$ (gam/lít). Khi thời gian $t$ càng lớn, nồng độ muối trong bể tiến dần về giá trị $c$ (gam/lít). Tính giá trị $a + b + c$.