Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Bảng biến thiên sau đây là của hàm số nào?
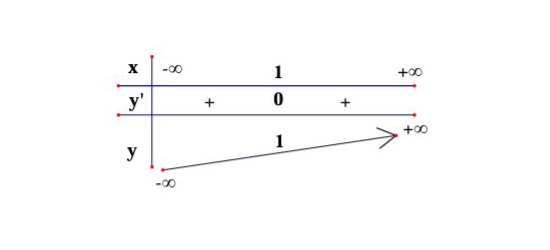
A. $y = -3x^2 + 1$.
B. $y = x^3 – 1$.
C. $y = x^4 + 3x^2 – 1$.
D. $y = \frac{x^3}{3} – x^2 + x + \frac{2}{3}$.
Câu 2: Cho hàm số $y = \frac{x^2 – 2x + 5}{x – 1}$. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng $(-1; 1) \cup (1; 3)$.
B. Hàm số nghịch biến trên khoảng $(-1; 3) \setminus {1}$.
C. Hàm số nghịch biến trên khoảng $(-1; 1)$ và $(1; 3)$.
D. Hàm số nghịch biến trên khoảng $(-\infty; -1)$.
Câu 3: Hàm số nào sau đây có bảng biến thiên như hình dưới đây?
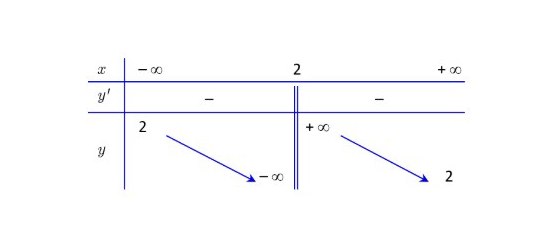
A. $y = \frac{2x – 7}{x – 2}$.
B. $y = \frac{2x + 1}{x + 2}$.
C. $y = \frac{2x + 1}{x – 2}$.
D. $y = \frac{1 – 2x}{x – 2}$.
Câu 4: Giá sử rằng chi phí sản xuất mỗi tuần của một công ty cho việc sản xuất $x$ sản phẩm được cho bởi $C(x) = 500 + 350x – 0,09x^2$ (triệu đồng). Chi phí để sản xuất sản phẩm thứ 301 gần với giá trị nào?
A. $296$ triệu.
B. $298$ triệu.
C. $975$ triệu.
D. $976$ triệu.
Câu 5: Một tia sáng chiếu tới gương phẳng và bị phản xa. Gọi $\vec{u}, \vec{v}, \vec{n}$ lần lượt là các vecto có độ dài bằng 1 dọc theo tia tới, tia phản xa và pháp tuyến như hình vẽ. Khẳng định nào sau đây đúng?
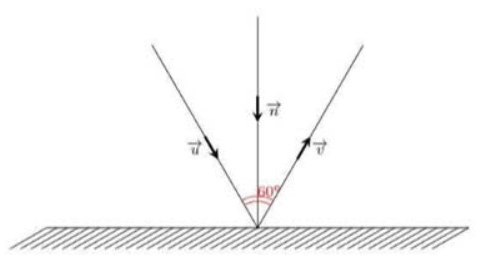
A. $\vec{v} – \vec{u} + \vec{n} = \vec{0}$.
B. $\vec{v} + \vec{u} – \sqrt{3}\vec{n} = \vec{0}$.
C. $\vec{v} – \vec{u} + \sqrt{3}\vec{n} = \vec{0}$.
D. $\vec{v} + \vec{u} – 3\vec{n} = \vec{0}$.
Câu 6: Cho hàm số $y = f(x)$ có bảng biến thiên như sau:
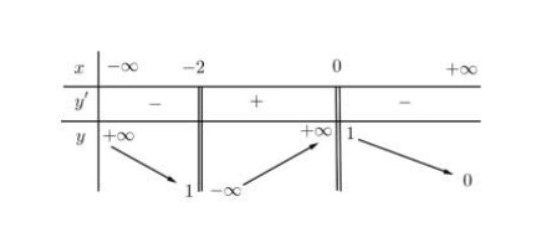
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng
A. $2$.
B. $1$.
C. $0$.
D. $3$.
Câu 7: Tìm giá trị nhỏ nhất của hàm số $f(x) = 3000(4-x) + 5000\sqrt{x^2 + 1}$ trên đoạn $[0; 4]$
A. $16000$.
B. $15000$.
C. $12000$.
D. $13000$.
Câu 8: Một căn phòng có dạng hình hộp chữ nhật $ABCD.A’B’C’D’$ với chiều rộng $AB = 4$, chiều dài $AD = 8$, chiều cao $AA’ = 10$ được gắn vào hệ trục $Oxyz$ như hình vẽ
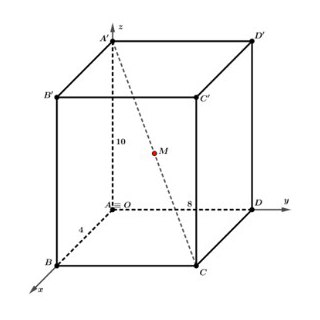
Người ta muốn treo một bóng đèn ở tâm hình hộp. Tìm tọa độ vị trí điểm $M$ để treo bóng đèn
A. $M(4; 5; 8)$.
B. $M(2; 4; 10)$.
C. $M(4; 4; 5)$.
D. $M(2; 4; 5)$.
Câu 9: Cho hàm số $y = f(x)$ có bảng biến thiên như sau
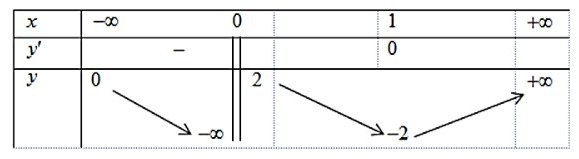
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A. $1$.
B. $2$.
C. $4$.
D. $3$.
Câu 10: Đường cong trong hình là đồ thị của hàm số nào dưới đây?
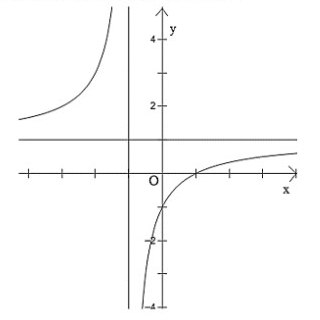
A. $y = \frac{x-1}{x+1}$.
B. $y = \frac{-2x+1}{2x+2}$.
C. $y = \frac{x^2+3x+1}{x+3}$.
D. $y = x^3 – 3x^2$.
Câu 11: Bác Minh thống kê lại thời gian sử dụng điện thoại của mình từ khi điện thoại được sạc đầy pin cho đến khi pin được sử dụng hết trong 30 ngày ở biểu đồ sau:
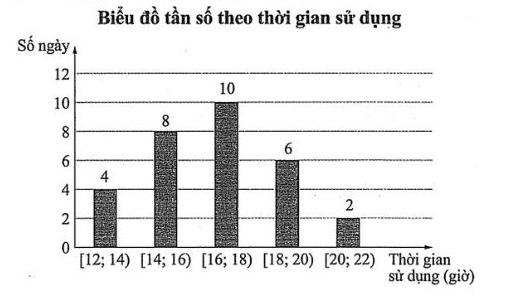
Trung vị của mẫu số liệu ghép nhóm trên thuộc nhóm nào sau đây:
A. $[20; 22)$.
B. $[16; 18)$.
C. $[14; 16)$.
D. $[18; 20)$.
Câu 12: Cho đồ thị của ba hàm số $y = f(x), y = f'(x), y = f”(x)$ được vẽ mô tả ở hình dưới đây. Hỏi đồ thị các hàm số $y = f(x), y = f'(x)$ và $y = f”(x)$ theo thứ tự, lần lượt trùng với đường cong nào?
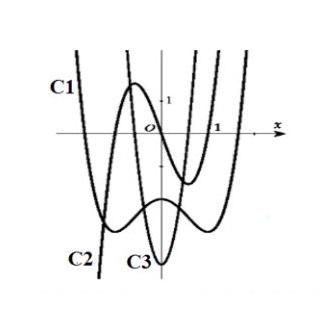
A. $(C_3); (C_2); (C_1)$.
B. $(C_2); (C_1); (C_3)$.
C. $(C_2); (C_3); (C_1)$.
D. $(C_1); (C_3); (C_2)$.
PHẦN II. Câu trắc nghiệm đúng sai
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1: Một hồ nước nhân tạo được xây dựng trong một công viên giải trí. Được mô hình hóa như hình bên dưới. Trong mô hình mô hình hóa, nó được giới hạn bởi các trục tọa độ và đồ thị của hàm số $y = f(x) = \frac{1}{10}(-x^3 + 9x^2 – 15x + 56)$.
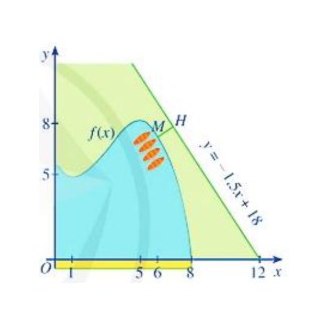
a) Đường dao ven hồ chạy dọc theo trục $Ox$ dài 800 mét.
b) Độ dài bờ hồ dọc theo trục $Oy$ dài 500 mét.
c) Trên đường dao ven hồ dọc theo trục $Ox$, có điểm mà khoảng cách theo phương vuông góc với trục $Ox$ đến bờ hồ đó diện tích là lớn nhất. Khoảng cách lớn nhất đó bằng 810 mét.
d) Trong công viên có một con đường chạy dọc theo đồ thị hàm số $y = -1,5x + 18$. Người ta dự định xây dựng bến thuyền để cho khoảng cách từ bến thuyền đến con đường này là ngắn nhất. Tung độ của điểm để xây bến thuyền này là 7,4.
Câu 2: Trong hệ trục tọa độ, $Oxyz$ cho bốn điểm $A(0; -2; 1), B(1; 0; -2), C(3; 1; -2), D(-2; -2; -1)$. Xét tính đúng sai của các mệnh đề sau
a) Bốn điểm $A, B, C, D$ không đồng phẳng
b) Tam giác $ACD$ là tam giác vuông tại A.
c) Góc giữa hai vecto $\overrightarrow{AB}$ và $\overrightarrow{CD}$ là góc tù.
d) Tam giác $ABD$ là tam giác cân tại $B$.
Câu 3: Trong hệ trục $Oxyz$, cho 3 điểm $A(1; 0; 0), B(0; 0; 1), C(2; 1; 1)$. Xét tính đúng sai của các mệnh đề:
a) Diện tích của tam giác $ABC$ bằng $\frac{\sqrt{6}}{2}$ (dvdt).
b) Gọi $D(x; y; z)$ sao cho tứ giác $ABCD$ là một hình bình hành khi đó $x + y + z = 3$.
c) Độ dài đường cao của tam giác $ABC$ hạ từ $A$ bằng $\frac{\sqrt{30}}{5}$ (đơn vị dài).
d) Thể tích của khối chóp $S.ABCD$ với đỉnh $S(0; 3; 4)$ bằng 2 (dvtt).
Câu 4: Cho hàm số $y = \frac{x^2 + 2x + 2}{x + 1}$ có đồ thị (C). Xét tính đúng sai của các mệnh đề sau.
a) Hàm số nghịch biến trên khoảng $(-2; -1)$.
b) Gọi $y_1, y_2$ lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số. Khi đó $y_1 – y_2 = 4$.
c) Phương trình đường thẳng đi qua hai điểm cực trị là $y = 2x + 2$.
d) Tiệm cận xiên của đồ thị (C) của hàm số trên có phương trình là $d: y = x$.
PHẦN III. Câu trắc nghiệm trả lời ngắn
Thí sinh trả lời từ câu 1 đến câu 6
Câu 1: Cho hình lập phương $ABCD.A’B’C’D’$. Gọi $M, N$ lần lượt là trung điểm $A’D’$ và $C’D’$. Gọi $\varphi$ là góc giữa hai vecto $\overrightarrow{MN}$ và $\overrightarrow{AB}$. Số đo của góc $\varphi$ bằng bao nhiêu độ?
Câu 2: Một người ở mặt đất điều khiển hai flycam để phục vụ một chương trình của đài truyền hình. Flycam I ở vị trí $A$ cách vị trí điều khiển 150 m về phía nam và 200 m về phía đông, đồng thời cách mặt đất 50 m. Flycam II ở vị trí $B$ cách vị trí điều khiển 180 m về phía bắc và 240 m về phía tây, đồng thời cách mặt đất 60 m. Chọn hệ trục tọa độ $Oxyz$ với gốc $O$ là vị trí điều khiển, mặt phẳng $(Oxy)$ trùng với mặt đất, trục $Ox$ có hướng trung với hướng nam, trục $Oy$ trung với hướng đông, trục $Oz$ vuông góc với mặt đất hướng lên bầu trời, đơn vị trên mỗi trục tính bằng mét. Khoảng cách giữa hai flycam đó bằng bao nhiêu mét (làm tròn đến hàng đơn vị)?
Câu 3: Một con cá hồi bơi ngược dòng nước để vượt một khoảng cách là 300 km. Vận tốc dòng nước là 6 km/h. Nếu vận tốc bơi của cá khi nước đứng yên là $v$ (km/h) thì năng lượng tiêu hao của cá trong $t$ giờ được cho bởi công thức $E(v) = cv^3t$ (trong đó $c$ là hằng số dương, $E$ được tính bằng đơn vị Jun). Cá bơi ngược dòng quãng đường 300 km trong khoảng thời gian $t$ với vận tốc bằng bao nhiêu để năng lượng tiêu hao là thấp nhất?
Câu 4: Cho hàm số bậc ba $y = ax^3 + bx^2 + cx + d$ có đồ thị như hình vẽ dưới đây.
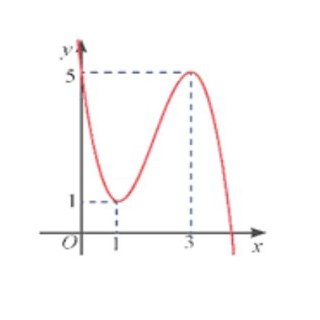
Giá trị của $a + b + c$ là
Câu 5: Một chiếc máy đo đạc trắc địa được đặt trên một giá đỡ ba chân với điểm đặt $S(0; 0; 4)$ và các điểm tiếp xúc với mặt đất của ba chân lần lượt là $A(-2; 0; 0), B(1; \sqrt{3}; 0), C(1; -\sqrt{3}; 0)$ (đơn vị $cm$). Biết rằng trọng lực tác dụng lên chiếc máy có độ lớn là 30N và được phân bố thành ba lực $\overrightarrow{F_1}, \overrightarrow{F_2}, \overrightarrow{F_3}$ có độ lớn bằng nhau như hình dưới
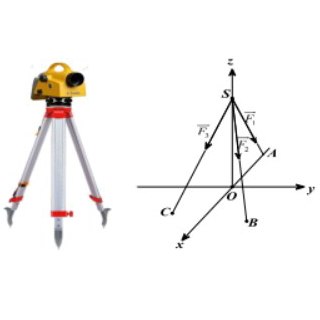
Biết rằng tích vô hướng của $\overrightarrow{F_1}.\overrightarrow{F_2}$ (mỗi $cm$ biểu diễn $1N$) bằng $\frac{a}{b}$ (với a,b là các số nguyên dương và $\frac{a}{b}$ là phân số tối giản). Khi đó $a.b$ bằng?
Câu 6: Một quả cầu sắt có bán kính 10cm được phủ bởi một lớp bằng đồng đều có độ dày 5cm. Biết rằng lớp bằng này tan chảy với tốc độ 50 cm³/phút. Cho biết công thức tính thể tích của khối cầu là $V = \frac{4}{3}\pi R^3$, trong đó $R$ là bán kính của khối cầu. Tốc độ giảm độ dày của bằng là $x cm$/phút. Khi độ giá trị của $x$ bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm)

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh

