PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn

Câu 1: Cho hàm số $y = f(x)$ là một nguyên hàm của hàm số $y = x^3$. Phát biểu nào sau đây đúng?
A. $f(x) = \frac{x^4}{4} + C$
B. $f(x) = 3x^2$
C. $f(x) = 4x^3$
D. $f(x) = \frac{x^4}{4}$

Câu 2: Trong không gian với hệ tọa độ $Oxyz$, phương trình nào sau đây là phương trình tổng quát của mặt phẳng
A. $2x + y^2 + z + 1 = 0$
B. $x^2 + y + z + 2 = 0$
C. $2x + y + z + 3 = 0$
D. $2x + y + z + 4 = 0$

Câu 3: Trong không gian với hệ tọa độ $Oxyz$, phương trình nào sau đây là phương trình chính tắc của đường thẳng?
A. $\frac{x – 2}{3} = \frac{y – 1}{z} = \frac{z – 5}{4}$
B. $\frac{x – 9}{7} = \frac{y – 8}{-1} = \frac{z – 6}{-2}$
C. $\frac{x – 6}{3} = \frac{y – 3}{4} = \frac{z – 5}{z}$
D. $\frac{x – 1}{y} = \frac{y – 2}{5} = \frac{z – 3}{4}$

Câu 4: Trong không gian với hệ tọa độ $Oxyz$, phương trình nào sau đây là phương trình mặt cầu
A. $(x^2 – 8)^2 + (y – 12)^2 + (z – 24)^2 = 9^2$
B. $(x – 9)^2 + (y^2 – 10)^2 + (z – 11)^2 = 12^2$
C. $(x – 13)^2 + (y – 24)^2 – (z – 36)^2 = 7^2$
D. $(x – 1)^2 + (y – 2)^2 + (z – 3)^2 = 5^2$

Câu 5: Cho hai biến cố A và B. Xác suất của biến cố A với điều kiện biến cố B đã xảy ra được gọi là xác suất của A với điều kiện B, ký hiệu là $P(A|B)$. Phát biểu nào sau đây đúng?
A. Nếu $P(A) > 0$ thì $P(A|B) = \frac{P(A \cap B)}{P(A)}$
B. Nếu $P(B) > 0$ thì $P(A|B) = \frac{P(A \cap B)}{P(B)}$
C. Nếu $P(A \cap B) > 0$ thì $P(A|B) = \frac{P(A)}{P(A \cap B)}$
D. Nếu $P(A \cap B) > 0$ thì $P(A|B) = \frac{P(B)}{P(A \cap B)}$

Câu 6: Cho hàm số $y = f(x)$ liên tục, không âm trên đoạn $[a; b]$ như hình 3. Hình phẳng $H$ giới hạn bởi đồ thị hàm số $y = f(x)$, trục hoành và hai đường thẳng $x = a$; $x = b$ quay quanh trục $Ox$ tạo thành một khối tròn xoay có thể tích bằng

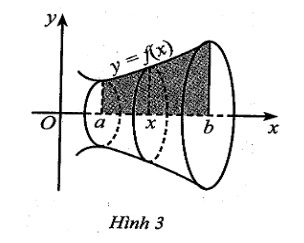
A. $V = \pi \int_a^b f(x) dx$
B. $V = \int_a^b [f(x)] dx$
C. $V = \int_a^b [f(x)]^2 dx$
D. $V = \pi \int_a^b [f(x)]^2 dx$

Câu 7: Họ nguyên hàm của hàm số $y = e^x \left( 2 + \frac{e^{-x}}{\cos^2 x} \right)$ là
A. $2e^x – \tan x + C$
B. $2e^x – \tan x + C$
C. $2e^x + \tan x + C$
D. $2e^x + \frac{1}{\cos x} + C$

Câu 8: Trong không gian $Oxyz$, cho hai điểm $A(2;4;1), B(-2;2;-3)$. Phương trình mặt cầu đường kính $AB$ là
A. $x^2 + (y-3)^2 + (z+1)^2 = 9$
B. $x^2 + (y-3)^2 + (z-1)^2 = 36$
C. $x^2 + (y+3)^2 + (z-1)^2 = 9$
D. $x^2 + (y-3)^2 + (z+1)^2 = 36$

Câu 9: Trong không gian $Oxyz$, cho hai điểm $M(1;0;1)$ và $N(3;2;-1)$. Đường thẳng $MN$ có phương trình tham số là
A. $\begin{cases} x = 1 + t \\ y = 2t \\ z = 1 + t \end{cases}$
B. $\begin{cases} x = 1 + t \\ y = t \\ z = 1 + t \end{cases}$
C. $\begin{cases} x = 1 + t \\ y = t \\ z = 1 – t \end{cases}$
D. $\begin{cases} x = 1 – t \\ y = t \\ z = 1 + t \end{cases}$

Câu 10: Cho $\int_{0}^{\pi/2} f(x) dx = 5$. Tính $I = \int_{0}^{\pi/2} [f(x) + 2 \sin x] dx$
A. 7
B. $5 + \frac{\pi}{2}$
C. $5 + \pi$
D. 3

Câu 11: Biết $\int_{1}^{3} \frac{x + 2}{x} dx = a + b \ln c$, với $a, b, c \in \mathbb{R}, c < 9$. Tính tổng $S = a + b + c$
A. 5
B. 6
C. 7
D. 8

Câu 12: Cho hai biến cố $A, B$ sao cho $P(A) = 0,5; P(B) = 0,7; P(A | B) = 0,3$. Tính $P(B | A)$
A. $\frac{5}{7}$
B. $\frac{3}{7}$
C. $\frac{6}{7}$
D. $\frac{21}{50}$

PHẦN II. Câu trắc nghiệm đúng sai

Câu 1: Trong không gian tọa độ $Oxyz$, cho hai mặt phẳng $(P_1):2x + y + 2z – 1 = 0$ và $(P_2):x – 2y – 2z – 7 = 0$

a) Vectơ có tọa độ $(2;2;1)$ là một vectơ pháp tuyến của mặt phẳng $(P_1)$

b) Vectơ có tọa độ $(1;-2;-2)$ là một vectơ pháp tuyến của mặt phẳng $(P_2)$

c) Góc giữa hai mặt phẳng $(P_1)$ và $(P_2)$ bằng $116^\circ$

Câu 2: Năm 2001, Cộng đồng Châu Âu có làm một đợt kiểm tra rất rộng rãi các con bò để phát hiện những con bị bệnh bò điên. Người ta tiến hành một loại xét nghiệm và cho kết quả như sau: Khi con bò bị bệnh bò điên thì xác suất để ra phản ứng dương tính trong xét nghiệm là $70\%$; còn khi con bò không bị bệnh thì xác suất để xảy ra phản ứng dương tính trong xét nghiệm đó là $10\%$. Biết rằng tỉ lệ bò bị mắc bệnh bò điên ở Hà Lan là 1,3 con trên 100000 con. Gọi $X$ là biến cố một con bò bị bệnh bò điên, $Y$ là biến cố một con bò phản ứng dương tính với xét nghiệm.

a) $P(X) = 13.10^{-6}$

b) $P(Y|X) = 0.07$

c) $P(Y|\overline{X}) = 0.1$

d) $P(Y \cap X) = 91.10^{-9}$

Câu 3: Một xe ô tô đang chạy với vận tốc $65 km/h$ thì người lái xe bất ngờ phát hiện chướng ngại vật trên đường cách đó $50 m$. Người lái xe phản ứng một giây, sau đó đạp phanh khẩn cấp. Kể từ thời điểm này, ô tô chuyển động chậm dần đều với tốc độ $v(t) = -10t + 20(m/s)$, trong đó $t$ là thời gian tính bằng giây kể từ lúc đạp phanh. Gọi $s(t)$ là quãng đường xe ô tô đi được trong $t$ (giây) kể từ lúc đạp phanh.

a) Quãng đường $s(t)$ mà xe ô tô đi được trong thời gian $t$ (giây) là một nguyên hàm của hàm số $v(t)$

b) $s(t) = -5t^2 + 20t$

c) Thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là $20$ giây

d) Xe ô tô đó không va vào chướng ngại vật ở trên đường

Câu 4: Trong không gian tọa độ $Oxyz$, cho mặt phẳng $(P):x + 2y – 2z + 3 = 0$ và đường thẳng $d: \frac{x – 1}{2} = \frac{y + 1}{-1} = \frac{z}{1}$

a) Một pháp vectơ của mặt phẳng $(P)$ là $\vec{n} = (2;4;-4)$

b) Đường thẳng $d$ vuông góc với đường thẳng $d’: \frac{x}{3} = \frac{y + 1}{2} = \frac{z}{-4}$

c) Góc giữa $d$ và $(P)$ gần bằng $15^\circ 47′ 35,41”$

d) Phương trình mặt phẳng $(Q)$ chứa đường thẳng $d$ và vuông góc với $(P)$ là $x + y + z + 1 = 0$

PHẦN III. Câu trắc nghiệm trả lời ngắn

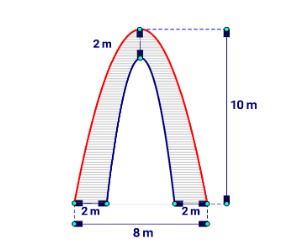
Câu 1: Một cổng có hình dạng như hình vẽ với viền ngoài và trong là hai đường cong dạng parabol cùng trục đối xứng (tham khảo hình vẽ dưới đây). Nhà trường dự định sơn mặt ngoài cổng (phần tô đậm) với chi phí nhân công là 30.000 đồng/m². Tính số tiền nhà trường trả cho nhân công (đơn vị: nghìn đồng)

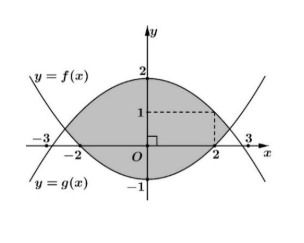
Câu 2: Bạn Hải nhận thiết kế logo hình con mắt (phần được tô đậm) cho một cơ sở y tế: Logo là hình phẳng giới hạn bởi hai parabol $y = f(x)$ và $y = g(x)$ như Hình 2 (đơn vị trên mỗi trục toạ độ là đề-xi-mét). Bạn Hải cần tính diện tích của logo để báo giá cho cơ sở y tế đó trước khi kí hợp đồng. Diện tích của logo là bao nhiêu đề-xi-mét vuông (làm tròn kết quả đến hàng phần mười).

Câu 3: Trong không gian $Oxyz$, đài kiểm soát không lưu sân bay có tọa độ $O(0;0;0)$, đơn vị trên mỗi trục tính theo kilômét. Một máy bay chuyển động hướng về đài kiểm soát không lưu, bay qua hai vị trí $A(500;-250;150)$, $B(200;-200;100)$. Khi máy bay ở gần đài kiểm soát nhất, tọa độ của vị trí máy bay là $(a;b;c)$. Giá trị của biểu thức $-3a – b – c$ là bao nhiêu? (làm tròn kết quả đến hàng đơn vị)

Câu 4: Một công ty dược phẩm giới thiệu một dụng cụ để kiểm tra sớm bệnh sốt xuất huyết. Về báo cáo kiểm định chất lượng của sản phẩm, họ cho biết như sau: Số người được thử là 8.000, trong số đó có 1.200 người đã bị nhiễm bệnh sốt xuất huyết và có 6.800 người không bị nhiễm bệnh sốt xuất huyết. Nhưng khi kiểm tra lại bằng dụng cụ của công ty, trong 1.200 người đã bị nhiễm bệnh sốt xuất huyết, có 70% số người đó cho kết quả dương tính, còn lại cho kết quả âm tính. Trong 6.800 người không bị nhiễm bệnh sốt xuất huyết, có 5% số người đó cho kết quả dương tính, còn lại cho kết quả âm tính. Xác suất mà một bệnh nhân với kết quả kiểm tra dương tính là bị nhiễm bệnh sốt xuất huyết bằng bao nhiêu? (viết kết quả dưới dạng số thập phân và làm tròn đến hàng phần trăm)

Câu 5: Có hai đội thi đấu môn Bắn súng. Đội I có 6 vận động viên, đội II có 8 vận động viên. Xác suất đạt huy chương vàng của mỗi vận động viên đội I và đội II tương ứng là 0,65 và 0,55. Chọn ngẫu nhiên một vận động viên trong hai đội. Giả sử vận động viên được chọn đạt huy chương vàng. Tính xác suất để vận động viên này thuộc đội I.

Câu 6: Trong không gian $Oxyz$, cho các đường thẳng:
$(d_1): \frac{x-3}{1} = \frac{y+1}{-2} = \frac{z+1}{1}$,
$(d_2): \frac{x-1}{1} = \frac{y+1}{-2} = \frac{z-1}{1}$,
$(d_3): \frac{x-1}{2} = \frac{y+1}{1} = \frac{z-1}{1}$,
$(d_4): \frac{x-1}{1} = \frac{y+1}{-1} = \frac{z-1}{1}$.
Tính số đường thẳng trong bốn đường thẳng trên có vectơ chỉ phương vuông góc với vectơ $\vec{u} = (1; -2; 1)$.

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh