PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn

Câu 1: Nguyên hàm của hàm số $f(x) = \frac{1}{5x – 2}$ là
A. $\int \frac{dx}{5x – 2} = \ln|5x – 2| + C$
B. $\int \frac{dx}{5x – 2} = 5\ln|5x – 2| + C$
C. $\int \frac{dx}{5x – 2} = \frac{1}{5}\ln|5x – 2| + C$
D. $\int \frac{dx}{5x – 2} = -\frac{1}{2}\ln|5x – 2| + C$

Câu 2: Nguyên hàm của hàm số $f(x) = x^2 + \frac{2}{x^2}$ là
A. $\int f(x) dx = \frac{x^3}{3} – \frac{1}{x} + C$
B. $\int f(x) dx = \frac{x^3}{3} + \frac{1}{x} + C$
C. $\int f(x) dx = \frac{x^3}{3} – \frac{2}{x} + C$
D. $\int f(x) dx = \frac{x^3}{3} + \frac{2}{x} + C$

Câu 3: Gọi $F(x)$ là nguyên hàm của hàm số $f(x) = \sin x + \cos x$ và thoả mãn $F(\frac{\pi}{2}) = 2$. Khi đó, $F(x)$ là
A. $F(x) = \cos x – \sin x + 3$
B. $F(x) = -\cos x + \sin x + 3$
C. $F(x) = -\cos x + \sin x – 1$
D. $F(x) = -\cos x + \sin x + 1$

Câu 4: Hàm số $F(x) = \frac{x^3}{3} + e^x$ là một nguyên hàm của hàm số nào trong các hàm số sau đây?
A. $f(x) = x^2 + e^x$
B. $f(x) = 3x^2 + e^x$
C. $f(x) = \frac{x^4}{3} + e^x$
D. $f(x) = \frac{x^4}{12} + e^x$

Câu 5: Cho hàm số $f(x)$ có đạo hàm liên tục trên đoạn $[1; \ln 3]$ và thỏa mãn $f(1) = e^2$, $\int_{1}^{\ln 3} f'(x) dx = 9 – e^2$. Tính giá trị của $f(\ln 3)$
A. $f(\ln 3) = -9$
B. $f(\ln 3) = 9$
C. $f(\ln 3) = 2e^2 – 9$
D. $f(\ln 3) = 9 – 2e^2$

Câu 6: Cho hình phẳng trong hình bên dưới (phần tô đậm) quay quanh trục hoành. Thể tích khối tròn xoay tạo thành được tính theo công thức nào trong các công thức sau đây?

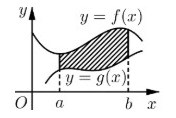
A. $V = \pi \int_{a}^{b} [g^2(x) – f^2(x)] dx$
B. $V = \pi \int_{a}^{b} [f^2(x) – g^2(x)] dx$
C. $V = \pi \int_{a}^{b} [f(x) – g(x)] dx$
D. $V = \pi \int_{a}^{b} [f(x) – g(x)]^2 dx$

Câu 7: Trong không gian $Oxyz$, cho mặt phẳng $(P): x – 2y + 3z – 5 = 0$. Một vector pháp tuyến của mặt phẳng $(P)$ là?
A. $\vec{n_2} = (1; -2; -3)$
B. $\vec{n_3} = (-1; 2; -3)$
C. $\vec{n_4} = (1; -2; -3)$
D. $\vec{n_1} = (1; 2; 3)$

Câu 8: Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A(2; 0; -1)$, $B(1; -1; 3)$ và mặt phẳng $(P): 3x + 2y – z + 5 = 0$. Mặt phẳng $(\alpha)$ đi qua $A, B$ và vuông góc với $(P)$ có phương trình
A. $(\alpha): -7x + 11y + z – 3 = 0$
B. $(\alpha): 7x – 11y + z – 1 = 0$
C. $(\alpha): -7x + 11y + z + 15 = 0$
D. $(\alpha): 7x – 11y – z + 1 = 0$

Câu 9: Trong không gian tọa độ $Oxyz$, cho đường thẳng $d: \frac{x – 2}{-1} = \frac{y – 1}{2} = \frac{z + 3}{1}$. Vector nào dưới đây là một vector chỉ phương của $d$?
A. $\vec{U_1} = (2; 1; -3)$
B. $\vec{U_2} = (-2; -1; 3)$
C. $\vec{U_3} = (-1; 2; 1)$
D. $\vec{U_4} = (-1; 2; -1)$

Câu 10: Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $(S): (x + 1)^2 + (y – 2)^2 + (z – 1)^2 = 9$. Tọa độ tâm $I$ và bán kính $R$ của $(S)$ là
A. $I(-1; 2; 1)$ và $R = 3$
B. $I(1; -2; -1)$ và $R = 3$
C. $I(-1; 2; 1)$ và $R = 9$
D. $I(1; -2; -1)$ và $R = 9$

Câu 11: Cho hai biến cố $A$ và $B$ có xác suất $P(A) = 0,4; P(B) = 0,7; P(A \cap B) = 0,3$. Xác suất $P(A | B)$ bằng

Câu 12: Trong hộp có 3 viên bi màu trắng và 7 viên bi màu đỏ. Lấy lần lượt mỗi lần một viên theo cách lấy không trả lại. Xác suất để viên bi lấy lần thứ hai là màu đỏ nếu biết rằng viên bi lấy lần thứ nhất cũng là màu đỏ là
A. $\frac{4}{7}$
B. $\frac{3}{7}$
C. $\frac{3}{4}$
D. $\frac{7}{10}$

PHẦN II. Câu trắc nghiệm đúng sai

Câu 1: Cho hình phẳng $(H)$ giới hạn bởi các đồ thị hàm số $y = x^3 – 3x – 4$ và $y = x – 4$ quay $(H)$ quanh trục hoành. Các mệnh đề sau đây đúng hay sai?

a) Diện tích hình phẳng $(H)$ là $S = \int_{-2}^{2} [(x^3 – 3x – 4) – (x – 4)] dx$

b) Thể tích khối tròn xoay được sinh ra là $V = \int_{-2}^{2} [(x^3 – 3x – 4)^2 – (x – 4)^2] dx$

c) Diện tích hình phẳng $(H)$ là $S = 8$

d) Thể tích khối tròn xoay được sinh ra là $V = 64\pi$

Câu 2: Cho $f(x)$, $g(x)$ là hai hàm số liên tục trên $\mathbb{R}$ và các số thực $a, b, c$. Các mệnh đề sau đây đúng hay sai?

a) $\int_{a}^{b} f(x) dx = \int_{a}^{b} f(y) dy$

b) $\int_{a}^{b} f(x) g(x) dx = \int_{a}^{b} f(x) dx \cdot \int_{a}^{b} g(x) dx$

c) $\int_{a}^{c} f(x) dx = \int_{a}^{b} f(x) dx + \int_{b}^{c} f(x) dx$ với $b \in [a; c)$

d) $\int_{a}^{b} [f(x) + g(x)] dx = \int_{a}^{b} f(x) dx + \int_{c}^{b} g(x) dx$

Câu 3: Trong không gian tọa độ $Oxyz$, cho mặt cầu $(S): x^2 + y^2 + z^2 – 6x + 4y – 12 = 0$. Các mệnh đề sau đây đúng hay sai?

a) Mặt cầu $(S)$ có tâm $I(3; -2; 0)$ và bán kính $R = 8$

b) Điểm $K(1; -2; 0)$ thuộc mặt cầu $(S)$

c) Đường kính của mặt cầu bằng 10

d) Mặt phẳng $(P): 3x – 4y + 5z – 17 + 20\sqrt{2} = 0$ cắt $(S)$ theo một đường tròn có bán kính $r = 3$

Câu 4: Một công ty truyền thông đấu thầu 2 dự án. Khả năng trúng thầu của dự án 1 là 0,5 và dự án 2 là 0,6. Khả năng trúng thầu của 2 dự án là 0,4. Gọi $A, B$ lần lượt là biến cố trúng thầu dự án 1 và dự án 2. Các mệnh đề sau đây đúng hay sai?

a) $A$ và $B$ là hai biến cố độc lập

b) Xác suất công ty trúng thầu đúng 1 dự án là $0,3$

c) Biết công ty trúng thầu dự án 1, xác suất công ty trúng thầu dự án 2 là $0,4$

d) Biết công ty không trúng thầu dự án 1, xác suất công ty trúng thầu dự án 2 là $0,8$

PHẦN III. Câu trắc nghiệm trả lời ngắn

Câu 1: Một ô tô đang chạy với vận tốc 10 (m/s) thì người lái xe đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc $v(t) = 10 – 2t$ (m/s), trong đó $t$ là khoảng thời gian được tính bằng giây, kể từ lúc bắt đầu đạp phanh. Tính quãng đường ô tô di chuyển được trong 8 giây cuối cùng.

Câu 2: Mực nước trong hồ chứa của nhà máy điện thuỷ triều thay đổi trong suốt một ngày do nước chảy ra (khi thuỷ triều xuống) và nước chảy vào (khi thuỷ triều lên). Gọi $h(t)$ là mực nước trong hồ tại thời điểm $t$ giờ. Tốc độ thay đổi của mực nước trong hồ chứa được cho bởi hàm số $h'(t) = 216(5t^2 – 120t + 480)$, trong đó $t$ tính bằng giờ $(0 \leq t \leq 24)$, $h'(t)$ tính bằng mét/giờ. Biết rằng tại thời điểm $t = 0$ (giờ), mực nước trong hồ chứa là 6 m. Tính mực nước trong hồ tại thời điểm $t = 5$ (giờ). (Làm tròn kết quả đến hàng phần nghìn).

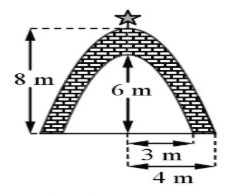
Câu 3: Nhà ông An cần sơn mặt trước của cổng có dạng như hình bên, các đường cong có dạng là Parabol với các kích thước được cho như hình. Biết giá thuê nhân công là 300.000 đồng/m². Hỏi ông An phải trả cho bên thi công bao nhiêu tiền (triệu đồng) để sơn cổng?

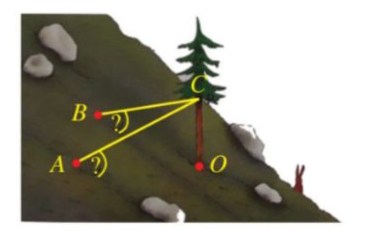
Câu 4: Trên một sườn núi (có độ nghiêng đều), người ta trồng một cây thông và muốn giữ nó không bị nghiêng bằng hai sợi dây neo như hình bên. Giả thiết cây thông mọc thẳng đứng và trong một hệ tọa độ phù hợp, các điểm $O$ (gốc cây thông) và $A, B$ (nơi buộc dây neo) có tọa độ tương ứng là $O(0; 0; 0)$, $A(3; -4; 2)$, $B(-5; -2; 1)$, đơn vị trên mỗi trục tọa độ là mét. Biết rằng hai dây neo đều được buộc vào cây thông tại điểm $(0; 0; 5)$ và được kéo căng tạo thành các đoạn thẳng. Tính tổng các góc tạo bởi mỗi dây neo và mặt phẳng sườn núi (làm tròn kết quả đến hàng đơn vị của độ).

Câu 5: Áo sơ mi An Phước trước khi xuất khẩu sang Mỹ phải qua 2 lần kiểm tra, nếu cả hai lần đều đạt thì chiếc áo đó mới đủ tiêu chuẩn xuất khẩu. Biết rằng bình quân 98% sản phẩm làm ra qua được lần kiểm tra thứ nhất, và 95% sản phẩm qua được lần kiểm tra đầu sẽ tiếp tục qua được lần kiểm tra thứ hai. Tìm xác suất để 1 chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu?

Câu 6: Một gia đình có 2 đứa trẻ. Biết rằng có ít nhất 1 đứa trẻ là con gái. Hỏi xác suất 2 đứa trẻ đều là con gái là bao nhiêu? Cho biết xác suất để một đứa trẻ là trai hoặc gái là bằng nhau.

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh