Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Họ tất cả các nguyên hàm của hàm số $f(x) = \frac{1}{\cos^2 x}$ là
A. $6\cot x + C$.
B. $\tan x + C$.
C. $-\cot x + C$.
D. $-\tan x + C$.
Câu 2: Tích phân $\int_0^1 x^{2024}dx$ có kết quả là
A. $\frac{1}{2024}$.
B. $2024$.
C. $2025$.
D. $\frac{1}{2025}$.
Câu 3: Hình (H) giới hạn bởi các đường $y = f(x)$, $x = a$, $x = b$ $(a < b)$ và trục Ox. Khi quay (H) quanh trục Ox ta được một khối tròn xoay có thể tích tính bằng công thức sau
A. $V = \pi \int_a^b |f(x)|dx$.
B. $V = \pi \int_a^b f(x)dx$.
C. $V = \pi \int_a^b f^2(x)dx$.
D. $V = \int_a^b f(x)dx$.
Câu 4: Diện tích hình phẳng (phần gạch sọc) trong hình sau bằng
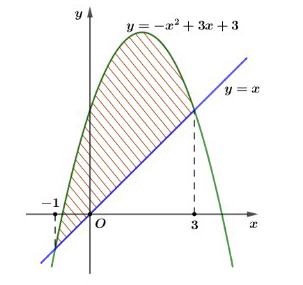
A. $S = \int_{-1}^3 (-x^2 + 2x + 3)dx$.
B. $S = \int_{-1}^1 (x^2 – 2x – 3)dx$.
C. $S = \int_{-1}^3 (-x^2 + 2x – 3)dx$.
D. $S = \int_{-1}^3 (-x^2 + 4x + 3)dx$.
Câu 5: Trong không gian Oxyz, một vec tơ pháp tuyến của mặt phẳng $3x + 2y – z + 1 = 0$ là
A. $\vec{n_1} = (3; 2; -1)$.
B. $\vec{n_4} = (3; -2; -1)$.
C. $\vec{n_2} = (-2; 3; 1)$.
D. $\vec{n_1} = (3; 2; 1)$.
Câu 6: Trong không gian Oxyz, cho đường thẳng $\Delta: \begin{cases} x = 1 + 2t \ y = -1 + 3t \ z = 2 – t \end{cases}$. Điểm nào dưới đây thuộc $\Delta$?
A. $(2; 3; -1)$.
B. $(-1; -4; 3)$.
C. $(-1; 1; -2)$.
D. $(2; -2; 4)$.
Câu 7: Trong không gian Oxyz, cho hai điểm $I(2; 4; -1)$ và $A(0; 2; 3)$. Phương trình mặt cầu có tâm $I$ và đi qua điểm $A$ là
A. $(x-2)^2 + (y-4)^2 + (z+1)^2 = 2\sqrt{6}$.
B. $(x+2)^2 + (y+4)^2 + (z-1)^2 = 2\sqrt{6}$.
C. $(x+2)^2 + (y+4)^2 + (z-1)^2 = 24$.
D. $(x-2)^2 + (y-4)^2 + (z+1)^2 = 24$.
Câu 8: Cho hai biến cố $A$ và $B$ là hai biến cố độc lập, với $P(A) = 0,2024$, $P(B) = 0,2025$. Xác suất của biến cố $A \cup B$ là
A. $0,7976$.
B. $0,7975$.
C. $0,2025$.
D. $0,2024$.
Câu 9: Một bình đựng 5 viên bi kích thước và chất liệu giống nhau, chỉ khác nhau về màu sắc. Trong đó có 3 viên bi xanh và 2 viên bi đỏ. Lấy ngẫu nhiên từ bình ra một viên bi ta được viên bi màu xanh, rồi lại lấy ngẫu nhiên ra một viên bi nữa. Tính xác suất để lấy được viên bi đỏ ở lần thứ hai.
A. $\frac{1}{5}$.
B. $\frac{2}{3}$.
C. $\frac{1}{2}$.
D. $\frac{2}{5}$.
Câu 10: Cho hai biến cố $A$ và $B$, với $P(B) = 0,8$, $P(A|B) = 0,7$, $P(A|\overline{B}) = 0,45$. Xác suất của biến cố A là
A. $0,25$.
B. $0,65$.
C. $0,55$.
D. $0,5$.
Câu 11: Họ nguyên hàm của hàm số $f(x) = 2^x(2^x + 5)$ là
A. $\frac{2^x}{\ln 2}\left(-\frac{2^x}{\ln 2} + 5^x\right) + C$.
B. $1 + 5\left(\frac{2^x}{\ln 2}\right) + C$.
C. $x + 5\left(\frac{2^x}{\ln 2}\right) + C$.
D. $x + 5.2^x.\ln 2 + C$.
Câu 12: Trong không gian Oxyz, mặt phẳng đi qua điểm $A(1; -2; 2)$ và có véc-tơ pháp tuyến $\vec{n} = (3; -1; -2)$ có phương trình là
A. $3x – y – 2z – 1 = 0$.
B. $x – 2y + 2z + 1 = 0$.
C. $3x – y – 2z + 1 = 0$.
D. $x – 2y + 2z – 1 = 0$.
PHẦN II. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho $f(x)$, $g(x)$ là hai hàm số xác định và liên tục trên $\mathbb{R}$.
a) $\int_a^b f(x)dx = \int_a^b f(y)dy$.
b) $\int_a^b (f(x) + g(x))dx = \int_a^b f(x)dx + \int_a^b g(x)dx$.
c) $\int_a^b f(x)dx = \int_a^a f(x)dx$.
d) $\int_a^b (f(x)g(x))dx = \int_a^b f(x)dx \int_a^b g(x)dx$.
Câu 2: Cho hình phẳng được gạch chéo trong hình bên dưới.

a) Hình phẳng được gạch chéo trong hình trên được giới hạn các đồ thị $y = x^2 – 2x – 2$, $y = -x^2 + 2$, $x = -1, x = 2$.
b) Diện tích hình phẳng gạch chéo trong hình vẽ là $S = \int_{-1}^2 (-2x^2 + 2x + 4)dx$.
c) Diện tích hình phẳng gạch chéo trong hình vẽ là $S = \int_{-1}^2 |2x^2 – 2x – 4|dx$.
d) Hình phẳng được gạch chéo trong hình trên được giới hạn các đồ thị $y = x^2 – 2x – 2$, $y = -x^2 + 2$, $x = 0, x = 2$.
Câu 3: Trong không gian $Oxyz$, cho đường thẳng d có phương trình $\frac{x + 4}{4} = \frac{y + 3}{3} = \frac{z – 3}{1}$.
a) Đường thẳng d có một vecto chỉ phương là $\vec{u} = (4; 1; 3)$.
b) Đường thẳng d đi qua điểm M(-4; -3; 3).
c) Đường thẳng $d’: \begin{cases} x = 2 – 4t \ y = 3 – 3t \ z = -t \end{cases}$, $(t \in \mathbb{R})$ song song với đường thẳng d.
d) Điều kiện cần và đủ để mặt phẳng $(P): mx + y + z + 5m + 1 = 0$ $(m \in \mathbb{R})$ song song với đường thẳng d là $m = -1$.
Câu 4: Một chiếc hộp có 80 viên bi, trong đó có 50 viên bi màu đỏ và 30 viên bi màu vàng; các viên bi có kích thước và khối lượng như nhau. Sau khi kiểm tra, người ta thấy có 60% số viên bi màu đỏ có đánh số và 50% số viên bi màu vàng có đánh số, những viên bi còn lại không đánh số.
a) Số viên bi màu đỏ có đánh số là 30.
b) Số viên bi không đánh số là 35.
c) Lấy ra ngẫu nhiên một viên bi trong hộp. Xác suất để viên bi được lấy ra có đánh số là $\frac{3}{5}$.
d) Lấy ra ngẫu nhiên một viên bi trong hộp. Xác suất để viên bi được lấy ra không đánh số là $\frac{7}{16}$.
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Một ô tô đang chạy với vận tốc $10m/s$ thì gặp chướng ngại vật, người lái xe đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc $v(t) = -2t + 10(m/s)$, trong đó $t$ là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Tính quãng đường ô tô đi chuyển được trong 8 giây cuối cùng.

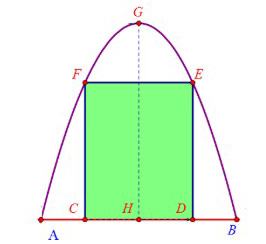
Câu 2: Chị Minh Hiền muốn làm một cái cổng hình Parabol như hình vẽ bên dưới. Chiều cao $GH = 4m$, chiều rộng $AB = 4m$, $AC = BD = 0,9m$. Chị Minh Hiền làm hai cánh cổng khi đóng lại là hình chữ nhật $CDEF$ tô đậm có giá là $1.200.000$ đồng$/m^2$, còn các phần để trống làm xiên hoa có giá là $900.000$ đồng$/m^2$. Hỏi tổng số tiền để làm hai phần nói trên bao nhiêu (Làm tròn đến hàng trăm ngàn)?
Câu 3: Trong không gian $Oxyz$, cho mặt phẳng $(P): 3x + 4y – 12z + 5 = 0$ và điểm $A(2; 4; -1)$. Trên mặt phẳng $(P)$ lấy điểm M. Điểm B thỏa mãn $\overrightarrow{AB} = 3\overrightarrow{AM}$. Tính khoảng cách d từ điểm B đến mặt phẳng $(P)$.
Câu 4: Một công ty sản xuất đèn LED trang trí cho các lễ hội. Một trong những sản phẩm mới là một đèn LED hình cầu với các dây đèn nằm đều bên trong. Để đảm bảo ánh sáng tỏa ra đều từ mọi hướng, tâm của đèn LED cần được đặt đúng tại vị trí của tâm hình cầu. Giá sở một quả cầu đèn LED có phương trình mặt cầu là: $(x-1)^2 + (y-3)^2 + (z+2)^2 = 49$. Một bóng đèn nhỏ nằm tại điểm $(4; 7; -2)$. Tính khoảng cách từ bóng đèn nhỏ đến tâm quả cầu đèn LED.
Câu 5: Bạn An làm 2 bài tập kế tiếp. Xác suất An làm đúng bài thứ nhất là $0,7$. Nếu An làm đúng bài thứ nhất thì khả năng làm đúng bài thứ hai là $0,8$ còn nếu An làm sai bài thứ nhất thì khả năng làm đúng bài thứ hai là $0,2$. Tính xác suất An làm đúng cả hai bài biết An làm đúng ít nhất một bài (kết quả cuối cùng làm tròn đến 2 chữ số thập phân).
Câu 6: Dựa trên dữ liệu lịch sử, ba trung tâm chẩn thương của ba bệnh viện lần lượt xử lý 50%, 30%, và 20% số ca. Xác suất một ca dẫn đến vụ kiện về sơ suất y tế tại mỗi trung tâm chẩn thương của ba bệnh viện trên lượng tăng là $0,001$, $0,005$, và $0,008$. Nếu một vụ kiện về sơ suất y tế được nộp, xác suất nó bắt nguồn từ trung tâm chẩn thương của bệnh viện thứ nhất là bao nhiêu? (kết quả cuối cùng làm tròn đến hai chữ số thập phân).

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh

