PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1: Hàm số $F(x)$ là một nguyên hàm của hàm số $f(x)$ trên khoảng $K$ nếu

A. $F'(x) = -f(x), \forall x \in K$.
B. $f'(x) = F(x), \forall x \in K$.
C. $F'(x) = f(x), \forall x \in K$.
D. $f'(x) = -F(x), \forall x \in K$.

Câu 2: Cho hàm số $y = f(x)$ có đạo hàm $f'(x)$ và $f'(x)$ liên tục trên đoạn $[a; b]$. Gọi $F(x)$ là một nguyên hàm của hàm số $f'(x)$ trên đoạn $[a; b]$. Chọn mệnh đề đúng.

A. $f(b) – f(a) = \int_a^b f'(x)dx$.
B. $F(b) – F(a) = \int_a^b f'(x)dx$.
C. $f(b) – f(a) = \int_a^b F(x)dx$.
D. $f'(b) – f'(a) = \int_a^b f'(x)dx$.

Câu 3: Nếu $\int_1^2 f(x)dx = 2$ thì $\int_1^2 [f(x) + 2x]dx$ bằng

A. $20$.
B. $18$.
C. $12$.
D. $10$.

Câu 4: Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$. Gọi S là diện tích hình phẳng giới hạn bởi các đường $y = f(x)$, $y = 0$, $x = -2$ và $x = 3$ (như hình vẽ). Mệnh đề nào dưới đây đúng?

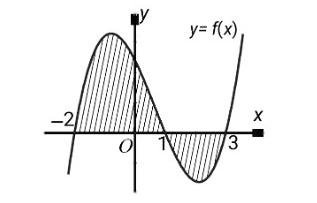
A. $S = -\int_{-2}^1 f(x)dx – \int_1^3 f(x)dx$.
B. $S = \int_{-2}^1 f(x)dx – \int_1^3 f(x)dx$.
C. $S = -\int_{-2}^1 f(x)dx + \int_1^3 f(x)dx$.
D. $S = \int_{-2}^1 f(x)dx + \int_1^3 f(x)dx$.

Câu 5: Gọi $(H)$ là hình phẳng giới hạn bởi các đường $y = x^2 + x – 2$, $y = 2x + 4$, $x = 1$ và $x = 4$. Cho diện tích hình phẳng $(H)$ bằng $\frac{a}{b}$ (dvdt), với $a, b \in \mathbb{N}$ và $\frac{a}{b}$ là phân số tối giản. Giá trị $T = a + b$ bằng:

A. $T = 67$.
B. $T = 25$.
C. $T = 76$.
D. $T = 23$.

Câu 6: Trong không gian $Oxyz$, cho mặt phẳng $(P)$ có phương trình $-2x + 2y – z – 3 = 0$. Mặt phẳng $(P)$ có vector pháp tuyến là

A. $(4; -4; 2)$.
B. $(-2; 2; -3)$.
C. $(-4; 4; 2)$.
D. $(0; 0; -3)$.

Câu 7: Trong không gian $Oxyz$, cho hai điểm $A(2; 4; 1), B(-1; 1; 3)$ và mặt phẳng $(P): x – 3y + 2z – 5 = 0$. Lập phương trình mặt phẳng $(Q)$ đi qua hai điểm $A$, $B$ và vuông góc với mặt phẳng $(P)$.

A. $2y + 3z – 11 = 0$.
B. $2x – 3y – 11 = 0$.
C. $x – 3y + 2z – 5 = 0$.
D. $3y + 2z – 11 = 0$.

Câu 8: Cho đường thẳng $\Delta$ có phương trình $\frac{x-1}{3} = \frac{y+3}{-2} = \frac{z-7}{5}$, điểm nào dưới đây thuộc đường thẳng $\Delta$?

A. $M(1; -3; 5)$.
B. $N(2; -1; 7)$.
C. $P(1; -3; 7)$.
D. $Q(3; -5; 7)$.

Câu 9: Trong các phương trình sau, phương trình nào là phương trình của mặt cầu tâm $I(-1; 2; -3)$ và đi qua điểm $M(0; 3; 2)$?

A. $(x-1)^2 + (y+2)^2 + (z-3)^2 = 13$.
B. $(x-1)^2 + (y+2)^2 + (z-3)^2 = \sqrt{13}$.
C. $(x+1)^2 + (y-2)^2 + (z+3)^2 = 27$.
D. $(x+1)^2 + (y-2)^2 + (z+3)^2 = \sqrt{27}$.

Câu 10: Cho hai biến cố $A$ và $B$ có $P(A) = 0,2; P(B) = 0,6; P(A|B) = 0,3$. Tính $P(\overline{AB})$.

A. $0,18$.
B. $0,42$.
C. $0,24$.
D. $0,02$.

Câu 11: Một nhóm học sinh có 30 học sinh, trong đó có 16 em học khá môn Toán, 25 em học khá môn Hóa học, 12 em học khá cả hai môn Toán và Hóa học. Chọn ngẫu nhiên một học sinh trong số đó. Tính xác suất để học sinh đó học khá môn Toán biết rằng học sinh đó học khá môn Hóa học.

A. $0,53$.
B. $0,75$.
C. $0,48$.
D. $0,84$.

Câu 12: Nếu hai biến cố $A, B$ thỏa mãn $P(A) = 0,3, P(B) = 0,6$ và $P(A|B) = 0,4$ thì $P(B|A)$ bằng

A. $0,5$.
B. $0,6$.
C. $0,8$.
D. $0,2$.

PHẦN II. Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Cho hàm số $y = f(x)$ xác định trên $(-\infty; 0)$. Biết rằng $f'(x) = 2x + \frac{1}{x^2}$.

a) $f(1) = 2$. Khi đó $f(x) = x^2 – \frac{1}{x} + 2$.

b) $f(1) = 0$. Phương trình $f(x) = 0$ có hai nghiệm.

c) Đồ thị hàm số $y = f(x)$ đi qua điểm $M(-1; 2)$. Khi đó $f(2) = \frac{13}{2}$.

d) $f(-2) = \frac{1}{4}$. Hàm số $g(x) = yf(x)$ có 3 điểm cực trị.

Câu 2: Trong không gian $Oxyz$, cho hai đường thẳng $d_1: \frac{x+2}{-1} = \frac{y-1}{-2} = \frac{z+3}{2}$; $d_2: \begin{cases} x = -1+t \ y = 3+t \ z = 2-mt \end{cases}$ ,và mặt phẳng $(P): 2x + 2y + z – 3 = 0$.

a) Khi $m = 0$, số đo góc giữa hai đường thẳng $d_1$ và $d_2$ bằng $135°$.

b) $\cos(d_1, Ox) = \frac{-1}{3}$.

c) Đường thẳng $\Delta$ đi qua gốc tọa độ $O$ và vuông góc với mặt phẳng $(P)$ tạo với đường thẳng $d_1$ một góc $\alpha$ có $\cos \alpha = \frac{4}{9}$.

d) Khi $m = \frac{a}{b}$, $a, b \in \mathbb{N}$, $\frac{a}{b}$ là phân số tối giản, số đo góc giữa hai đường thẳng $d_1$ và $d_2$ bằng $90°$. Giá trị biểu thức $a^2 + b^2 = 13$.

Câu 3: Trong mặt phẳng $(Oxyz)$

a) Mặt cầu $(S): x^2 + y^2 + z^2 – 2x + 4y + 1 = 0$ có tâm $I(1; -2; 0)$ và bán kính $R = 2$.

b) Mặt cầu $(S): 2x^2 + 2y^2 + 2z^2 – 4x + 8y – 12z = 0$ có tâm $I(2; -4; 6)$ và bán kính $R = 2\sqrt{14}$.

c) Mặt cầu đường kính $AB$ với $A(0; 1; -2)$ và $B(2; -1; -4)$ có tâm $I(1; 0; -3)$ và bán kính $R = 2\sqrt{5}$.

d) Mặt cầu tâm $I(1; 2; 4)$ tiếp xúc với mặt phẳng $(P): x + y – z – 2 = 0$ có bán kính $R = \sqrt{3}$.

Câu 4: Có hai hộp đựng các viên bi cùng kích thước và khối lượng. Hộp thứ nhất chứa 5 viên bi đỏ và 5 viên bi xanh, hộp thứ hai chứa 6 viên bi đỏ và 4 viên bi xanh. Lấy ngẫu nhiên một viên bi từ hộp thứ nhất chuyển sang hộp thứ hai, sau đó lấy ra ngẫu nhiên một viên bi từ hộp thứ hai. Gọi $A$ là biến cố “Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi đỏ” và $B$ là biến cố “Viên bi được lấy ra từ hộp thứ hai là bi đỏ”. Các khẳng định sau đúng hay sai?

a) Xác suất của biến cố $B$ là $P(B) = 0,5$.

b) Giả sử viên bi lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi đỏ thì khi đó $P(A|B) = \frac{7}{11}$.

c) Gọi $\overline{B}$ là biến cố “Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi xanh” thì $P(A|\overline{B}) = \frac{7}{11}$.

d) Xác suất để viên bi được lấy ra từ hộp thứ hai là viên bi đỏ là $P(A) = \frac{13}{22}$.

PHẦN III. Câu trắc nghiệm trả lời ngắn.

Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: Một vật chuyển động dọc theo một đường thẳng sao cho vận tốc của nó tại thời điểm $t$ (giây) là $v(t) = t^2 – t – 6$ (mét/giây). Quãng đường (mét) vật đi được trong khoảng thời gian $1 \leq t \leq 4$ bằng (làm tròn tới hàng phần chục)

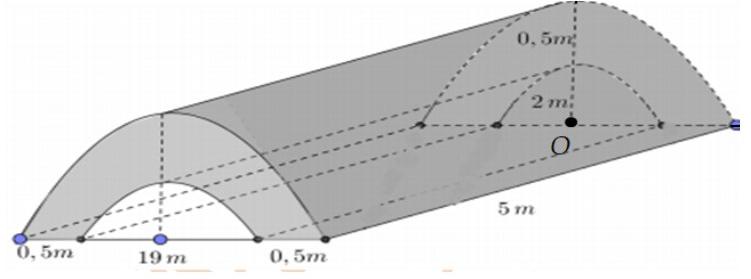
Câu 2: Trong chương trình nông thôn mới, tại một xã Y có xây một cây cầu bằng bê tông như hình vẽ. Tính thể tích khối bê tông để đổ cây cầu. (Đường cong trong hình vẽ là các đường Parabol)

Câu 3: Trong không gian $Oxyz$, cho mặt phẳng $(P): ax + by + cz – 27 = 0$ qua hai điểm $A(3; 2; 1)$ và $B(-3; 5; 2)$ và vuông góc với mặt phẳng $(Q): 3x + y + z + 4 = 0$. Tính tổng $S = a + b + c$.

Câu 4: Trong không gian với hệ tọa độ $Oxyz$, một cabin cáp treo ở Ba Nà Hill xuất phát từ điểm $A(-2; 1; 5)$ và chuyển động đều theo đường cáp có vector chỉ phương là $\vec{u} = (0; -2; 6)$ với tốc độ là $4$ m/s (đơn vị trên mỗi trục tọa độ là mét). Giả sử sau 5 (s) kể từ lúc xuất phát, cabin đến điểm $M$. Gọi tọa độ của điểm $M(a; b; c)$. Tính $a + 3b + c$

Câu 5: Trong không gian $Oxyz$, cho đường thẳng $\Delta: \frac{x-2}{-3} = \frac{y-1}{2} = \frac{z-1}{2}$, $(P): x + 2y – 2z – 2 = 0$, $(Q): x + 2y – 2z + 4 = 0$. Gọi mặt cầu $S(I, R)$ có tâm $I$ thuộc $\Delta$ và tiếp xúc với $(P), (Q)$. Khi đó đường kính của mặt cầu có giá trị bằng bao nhiêu?

Câu 6: Một người săn thỏ trong rừng, khả năng anh ta bắn trúng thỏ trong mỗi lần bắn tỷ lệ nghịch với khoảng cách bắn. Anh ta bắn lần đầu ở khoảng cách $20m$ với xác suất trúng thỏ là $0,5$; nếu bị trượt anh ta bắn viên thứ hai ở khoảng cách $30m$; nếu lại trượt anh ta bắn viên thứ ba ở khoảng cách $40m$. Tính xác suất để người thỏ săn bắn được thỏ.

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh