Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Họ nguyên hàm của hàm số $f(x) = \frac{1}{x^2} – x^2 – \frac{1}{3}$ là
A. $\frac{-x^4 + x^2 + 3}{3x} + C$.
B. $\frac{-2}{x^3} – 2x + C$.
C. $\frac{-x^4 + x^2 + 3}{3x} + C$.
D. $\frac{-x^3}{3} – \frac{1}{x} – \frac{x}{3} + C$.
Câu 2: Họ nguyên hàm của hàm số $f(x) = e.x^e + 4$ là
A. $101376$.
B. $e^2.x^{e-1} + C$.
C. $\frac{x^{e+1}}{e+1} + 4x + C$.
D. $\frac{e.x^{e-1}}{e+1} + 4x + C$.
Câu 3: Tính tích phân $I = \int_0^2 (2x + 1)dx$
A. $I = 5$.
B. $I = 6$.
C. $I = 2$.
D. $I = 4$.
Câu 4: Trong không gian $Oxyz$, mặt phẳng $(\alpha): x + 2y – z + 1 = 0$ đi qua điểm nào dưới đây?
A. $M(-1; 0; 0)$.
B. $N(0; -2; 0)$.
C. $P(1; -2; 1)$.
D. $Q(1; 2; -1)$.
Câu 5: Trong không gian Oxyz, cho đường thẳng $d: \frac{x-2}{-1} = \frac{y-1}{2} = \frac{z+3}{1}$. Vector nào dưới đây là một vector chỉ phương của $d$?
A. $\vec{u_1} = (2; 1; 1)$.
B. $\vec{u_2} = (1; 2; -3)$.
C. $\vec{u_3} = (1; -2; -1)$.
D. $\vec{u_4} = (2; 1; -3)$.
Câu 6: Trong không gian $Oxyz$, cho mặt cầu $(S)$ có phương trình: $x^2 + y^2 + z^2 – 2x – 4y + 6z – 2 = 0$. Tọa độ tâm $I$ và bán kính $R$ của mặt cầu $(S)$ là:
A. $I(1; 2; -3)$ và $R = 4$.
B. $I(1; -2; -3)$ và $R = 2\sqrt{3}$.
C. $I(-1; -2; -3)$ và $R = 2\sqrt{3}$.
D. $I(-1; -2; 3)$ và $R = 4$.
Câu 7: Cho hai biến cố $A$ và $B$, với $P(A) = 0,6, P(B) = 0,7, P(A \cap B) = 0,3$. Tính $P(A \cup B)$.
A. $\frac{3}{7}$.
B. $\frac{1}{2}$.
C. $\frac{6}{7}$.
D. $\frac{1}{7}$.
Câu 8: Cho hai biến cố $A$ và $B$ với $0 < P(B) < 1$. Công thức nào sau đây là công thức xác suất toàn phần?
A. $P(A) = P(B).P(A|B) + P(\overline{B}).P(A|\overline{B})$.
B. $P(A) = P(B).P(A|B) – P(\overline{B}).P(A|\overline{B})$.
C. $P(A) = P(B).P(A|B) + P(B).P(A|\overline{B})$.
D. $P(A) = P(B).P(A|B) – P(B).P(A|\overline{B})$.
Câu 9: Biết $\int_1^2 \frac{x+2}{x}dx = a + b\ln c$, với $a, b, c \in \mathbb{N}, c < 9$. Tính tổng $S = a + b + c$.
A. $S = 7$.
B. $S = 5$.
C. $S = 8$.
D. $S = 6$.
Câu 10: Cho đồ thị hàm số $y = f(x)$ như hình vẽ bên.
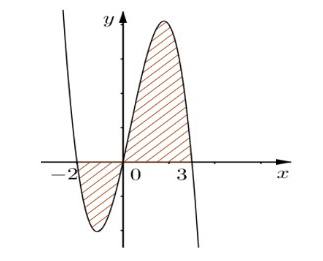
Diện tích $S$ của hình phẳng phần tô đậm trong hình được tính theo công thức nào sau đây?
A. $S = \int_{-2}^3 f(x)dx$.
B. $S = \int_{-2}^0 f(x)dx + \int_0^3 f(x)dx$.
C. $S = \int_{-2}^0 f(x)dx + \int_0^3 f(x)dx$.
D. $S = \int_0^3 f(x)dx + \int_0^3 f(x)dx$.
Câu 11: Trong không gian $Oxyz$, viết phương trình đường thẳng $\Delta$ đi qua $M(-1;1;0)$ và vuông góc với mặt phẳng $(Q): x-4y-z-2=0$?
A. $\begin{cases} x = 1-t \\ y = -4+t \\ z = -1 \end{cases}$
B. $\begin{cases} x = 1+t \\ y = 1-4t \\ z = -t \end{cases}$
C. $\begin{cases} x = -1+t \\ y = 1-4t \\ z = -t \end{cases}$
D. $\begin{cases} x = -1-t \\ y = 1-4t \\ z = t \end{cases}$
Câu 12: Trong không gian $Oxyz$, cho đường tròn $(C)$ tâm $O$ có bán kính bằng $2$ và nằm trong mặt phẳng $(xOy)$. Phương trình mặt cầu chứa đường tròn $(C)$ và đi qua điểm $A(0; 0; -4)$ là
A. $x^2 + y^2 + z^2 = \frac{25}{4}$.
B. $x^2 + y^2 + \left(z – \frac{3}{2}\right)^2 = \frac{25}{4}$.
C. $x^2 + y^2 + \left(z + \frac{3}{2}\right)^2 = \frac{25}{4}$.
D. $x^2 + y^2 + (z + 4)^2 = 1$.
PHẦN II. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho K là một khoảng trên R;F(x) là một nguyên hàm của hàm số f(x) trên K;G(x) là một nguyên hàm của hàm số g(x) trên K.
a) Nếu F(x) = G(x) thì f(x) = g(x)
b) Nếu f(x) = g(x) thì F(x) = G(x)
c) $\int f(x)dx = F(x) + C, C \in \mathbb{R}$
d) $\int f'(x)dx = F(x) + C, C \in \mathbb{R}$
Câu 2: Một vật trang trí có dạng một khối tròn xoay được tạo thành khi quay miền $(R)$ (phần gạch chéo trong hình vẽ bên) quanh trục $AB$. Miền $(R)$ được giới hạn bởi các cạnh $AB, AD$ của hình vuông $ABCD$ và các cung phần tử của các đường tròn bán kính bằng $1$ cm với tâm lần lượt là trung điểm của các cạnh $BC, AD$.
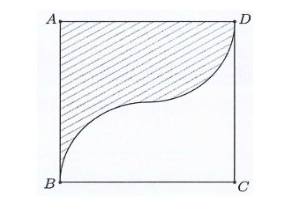
Chọn hệ trục tọa độ $Oxy$ với $A = O(0; 0)$, $B$ thuộc tia $Ox$, $D(0; 2)$ thuộc tia $Oy$. Các mệnh đề sau đúng hay sai?
a) $C(2; 2)$
b) Phương trình đường tròn đường kính $AD$ là $x^2 + (y-1)^2 = 1$
c) Phương trình đường tròn đường kính $BC$ là $(x+2)^2 + (y+1)^2 = 1$
d) Thể tích của vật trang trí đó khoảng $20,3 cm^3$ (kết quả làm tròn kết quả đến hàng phần mười).
Câu 3: Trong không gian với hệ trục tọa độ $Oxyz$, cho mặt cầu (S) có phương trình $x^2 + y^2 + z^2 – 2x + 6y + 1 = 0$.
1/ Mặt cầu có tâm $I$, bán kính $R$ là : $\begin{cases} I(1; -3; 0) \ R = 3 \end{cases}$.
2/ Điểm $M(4; -3)$ thuộc mặt cầu
3/ Mặt Cầu Tiếp xúc với truc Ox
4/ Mặt phẳng (P): $2x + y – 2z + 4 = 0$ Cắt Mặt cầu (S) theo đường tròn có đường kính bằng: 5
Câu 4: Một chiếc hộp có 80 viên bi, trong đó có 50 viên bi màu đỏ và 30 viên bi màu vàng; các viên bi có kích thước và khối lượng như nhau. Sau khi kiểm tra, người ta thấy có 60% số viên bi màu đỏ đánh số và 50% số viên bi màu vàng có đánh số, những viên bi còn lại không đánh số.
a) Số viên bi màu đỏ có đánh số là 30.
b) Số viên bi màu vàng không đánh số là 15.
c) Lấy ra ngẫu nhiên một viên bi trong hộp. Xác suất để viên bi được lấy ra có đánh số là $\frac{3}{5}$.
d) Lấy ra ngẫu nhiên một viên bi trong hộp. Xác suất để viên bi được lấy ra không có đánh số là $\frac{7}{16}$.
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Một xe mô tô phân khối lớn đang chạy với vận tốc 10m/s thì tăng tốc với gia tốc $a(t) = t^2 + 3t(m/s^2)$. Hỏi quãng đường của xe đi được trong quãng thời gian 10s đầu tiên sau khi tăng tốc?
Câu 2: Cho hàm số $f(x) = \begin{cases} 7-4x^3 & \text{khi } 0 < x < 1 \\ 4-2x & \text{khi } x > 1 \end{cases}$. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $f(x)$ và các đường thẳng $x = 0$, $x = 3$, $y = 0$.
Câu 3: Trong không gian với hệ tọa độ $Oxyz$, cho tam giác $ABC$ có $A(1; -1; 1)$, $B(2; 1; -2)$, $C(0; 0; 1)$. Gọi $H(a; b; c)$ là trực tâm của tam giác $ABC$. Tính giá trị biểu thức $P = a + 3b – c$.
Câu 4: Người ta muốn thiết kế một bồn chứa khí hoá lỏng hình cầu bằng phần mềm 3D. Cho biết phương trình bề mặt của bồn chứa là $(S): (x-12)^2 + (y-12)^2 + (z-12)^2 = 25$. Phương trình mặt phẳng chứa nắp là $(P): z = 16$.

Tính bán kính của nắp (Xem nắp bồn chứa như là hình tròn giao tuyến của mặt phẳng $(P)$ và mặt cầu $(S)$).
Câu 5: Một công ty bảo hiểm nhân thọ có 48% số người mua bảo hiểm ô tô là phụ nữ và có 36% số người mua bảo hiểm ô tô là phụ nữ trên 50 tuổi. Biết một người mua bảo hiểm ô tô là phụ nữ, tính xác suất người đó trên 50 tuổi.
Câu 6: Trong một kì thi tốt nghiệp trung học phổ thông, một tỉnh $X$ có 80% học sinh lựa chọn tổ hợp A00 (gồm các môn Toán, Vật lí, Hóa học). Biết rằng, nếu một học sinh chọn tổ hợp A00 thì xác suất để học sinh đó đỗ đại học là 0,6; còn nếu một học sinh không chọn tổ hợp A00 thì xác suất để học sinh đó đỗ đại học là 0,7. Chọn ngẫu nhiên một học sinh của tỉnh $X$ đã tốt nghiệp trung học phổ thông trong kì thi trên. Biết rằng học sinh này đã đỗ đại học. Tính xác suất để học sinh đó chọn tổ hợp A00.

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh

