PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1: Họ nguyên hàm của hàm số $f(x) = x^3$ là

A. $4x^4 + C$.
B. $3x^2 + C$.
C. $x^4 + C$.
D. $\frac{1}{4}x^4 + C$.

Câu 2: Nếu $\int_2^5 f(x)dx = 2$ thì $\int_2^5 3f(x)dx$ bằng

A. $6$.
B. $3$.
C. $18$.
D. $2$.

Câu 3: Cho biết tốc độ đi chuyển của vật theo thời gian tại mọi thời điểm $t \in [a; b]$ là $v(t)$. Khi đó quãng đường đi chuyển trong khoảng thời gian từ $a$ đến $b$ bằng

A. $s = \int_b^a v'(t)dt$.
B. $s = \int_a^b v'(t)dt$.
C. $s = \int_b^a v(t)dt$.
D. $s = \int_a^b v(t)dt$.

Câu 4: Diện tích $S$ của hình phẳng giới hạn bởi các đường $y = 2x^2$, $y = -1$, $x = 0$ và $x = 1$ được tính bởi công thức nào sau đây?

A. $S = \pi \int_0^1 (2x^2 + 1)dx$.
B. $S = \int_0^1 (2x^2 + 1)dx$.
C. $S = \int_0^1 (2x^2 – 1)dx$.
D. $S = \int_0^1 (2x^2 + 1)^2 dx$.

Câu 5: Cho hình phẳng $D$ giới hạn với đường cong $y = \sqrt{x^2 + 1}$, trục hoành và các đường thẳng $x = 0, x = 1$. Khối tròn xoay tạo thành khi quay $D$ quanh trục hoành có thể tích $V$ bằng

A. $V = 2$.
B. $V = \frac{4}{3}$.
C. $V = 2\pi$.
D. $V = \frac{4\pi}{3}$.

Câu 6: Trong không gian $Oxyz$, cho ba điểm $A(-1; 1; 1)$, $B(2; 1; 0)$, $C(1; -1; 2)$. Mặt phẳng đi qua $A$ và vuông góc với đường thẳng $BC$ có phương trình là

A. $3x + 2z + 1 = 0$.
B. $x + 2y – 2z – 1 = 0$.
C. $x + 2y – 2z + 1 = 0$.
D. $3x + 2z – 1 = 0$.

Câu 7: Trong không gian $Oxyz$, cho đường thẳng $d: \frac{x-3}{4} = \frac{y+1}{-2} = \frac{z+2}{3}$. Vecto nào dưới đây là một vecto chỉ phương của $d$?

A. $\vec{u_3} = (3; -1; -2)$.
B. $\vec{u_4} = (4; 2; 3)$.
C. $\vec{u_1} = (3; 1; 2)$.
D. $\vec{u_2} = (4; -2; 3)$.

Câu 8: Trong không gian $Oxyz$, cho mặt cầu $(S): x^2 + y^2 + z^2 + 2x – 2z – 7 = 0$. Bán kính của mặt cầu đã cho bằng

A. $\sqrt{7}$.
B. $3$.
C. $\sqrt{15}$.
D. $9$.

Câu 9: Cho hai biến cố $A$ và $B$ là hai biến cố độc lập, với $P(A) = 0,2024$, $P(B) = 0,2025$. Khi đó $P(A|B)$ bằng

A. $0,7976$.
B. $0,2024$.
C. $0,7975$.
D. $0,2025$.

Câu 10: Lớp Toán Sư Phạm có 95 Sinh viên, trong đó có 40 nam và 55 nữ. Trong kỳ thi môn Xác suất thống kê có 23 sinh viên đạt điểm giỏi (trong đó có 12 nam và 11 nữ). Gọi tên ngẫu nhiên một sinh viên trong danh sách lớp. Xác suất gọi được sinh viên đạt điểm giỏi môn Xác suất thống kê, biết rằng sinh viên đó là nữ, bằng

A. $\frac{1}{5}$.
B. $\frac{11}{23}$.
C. $\frac{12}{23}$.
D. $\frac{11}{19}$.

Câu 11: Một bình đựng 9 viên bi xanh và 7 viên bi đỏ. Lần lượt lấy ngẫu nhiên ra 2 bi, mỗi lần lấy 1 bi không hoàn lại. Xác suất để bị thứ 2 màu xanh, biết rằng bi thứ nhất màu đỏ, bằng

A. $\frac{3}{5}$.
B. $\frac{9}{16}$.
C. $\frac{9}{17}$.
D. $\frac{21}{80}$.

Câu 12: Cho hai biến cố $A$ và $B$, với $P(B) = 0,8$, $P(A|B) = 0,7$, $P(A|\overline{B}) = 0,45$. Xác suất $P(B|A)$ bằng

A. $\frac{56}{65}$.
B. $0,65$.
C. $0,25$.
D. $0,5$.

Phần II. Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Trong không gian $Oxyz$, gọi $I$ và $R$ lần lượt là tâm và bán kính mặt cầu $(S): (x+3)^2 + y^2 + (z-2)^2 = 16$.

a) Điểm $M(-1; 0; 3)$ nằm trong mặt cầu $(S)$.

b) Bán kính mặt cầu $(S)$ là $R = 4$.

c) Tọa độ tâm mặt cầu $(S)$ là $I(-3; 0; 2)$.

d) Mặt cầu $(S)$ cắt mặt phẳng $(Oxy)$ theo giao tuyến là đường tròn có bán kính bằng $10$.
**Câu 2:** Trong không gian $Oxyz$, cho điểm $M(-1; 3; 2)$ và mặt phẳng $(P): x – 2y + 4z + 2 = 0$.

a) Đường thẳng đi qua $M$ và vuông góc với $(P)$ có phương trình là $\frac{x+1}{1} = \frac{y-3}{-2} = \frac{z-2}{1}$.

b) Trục $Ox$ cắt mặt phẳng $(P)$ tại điểm $K(-2; 0; 0)$.

c) Gọi $N$ là giao điểm của $(P)$ và $Oy$. Đường thẳng $MN$ có phương trình tham số là $\begin{cases} x = -1+t \\ y = 3+2t \\ z = 2-2t \end{cases}$.

d) Đường thẳng $\Delta$ là giao tuyến của mặt phẳng $(P)$ và $(Oyz)$. Phương trình tham số của đường thẳng $\Delta$ là $\begin{cases} x = 0 \\ y = 3+2t \\ z = 1+t \end{cases}$.

**Câu 3:** Cho tứ diện $OABC$, có $OA, OB, OC$ đôi một vuông góc và $OA = 5, OB = 2, OC = 4$. Gọi $M, N$ lần lượt là trung điểm của $OB$ và $OC$. Chọn hệ tọa độ $Oxyz$ như hình vẽ bên dưới.

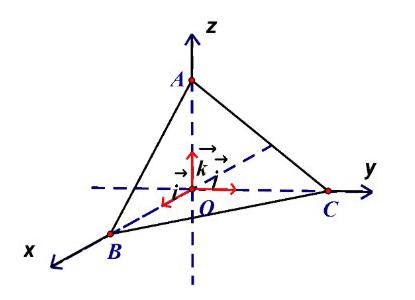
a) Tọa độ các điểm $A, B, C$ lần lượt là $(0; 0; 5), (2; 0; 0), (0; 2; 0)$

b) Mặt phẳng $(ABC)$ có phương trình là $\frac{x}{5} + \frac{y}{4} + \frac{z}{2} = 1$

c) Mặt phẳng $(ANM)$ có phương trình là $\frac{x}{1} + \frac{y}{2} + \frac{z}{5} = 1$

d) Gọi $G$ là trọng tâm tam giác $ABC$. Đường thẳng $d$ cắt $(AMN)$ tại $K$ và cắt $(ABC)$ tại $E$. Tỷ số $\frac{AK}{AE} = \frac{3}{5}$

**Câu 4:** Tỉ lệ phế phẩm của công ty là 10%. Trước khi đưa ra thị trường, các sản phẩm được kiểm tra bằng máy nhằm loại bỏ phế phẩm. Xác suất để máy nhận biết đúng chính phẩm là 95%, nhận biết đúng phế phẩm là 90%.

a) Tỉ lệ chính phẩm của công ty là $0,9$

b) Nếu gọi $H_1$ là biến cố “chọn được sản phẩm là chính phẩm” thì $P(H_1) = 0,1$

c) Tỉ lệ sản phẩm bị kết luận sai là $0,005$

d) Tỉ lệ phế phẩm của công ty trên thị trường là $0,12$

Phần III. Câu trắc nghiệm trả lời ngắn

**Câu 1:** Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng $(P):x+y-4z=0$, đường thẳng $d : \frac{x-1}{2} = \frac{y+1}{-1} = \frac{z-3}{1}$ và điểm $A(1; 3; 1)$ thuộc mặt phẳng $(P)$. Gọi $\Delta$ là đường thẳng đi qua $A$, nằm trong mặt phẳng $(P)$ và cách đường thẳng $d$ một khoảng cách lớn nhất. Gọi $\vec{u} = (a; b; 1)$ là một véc tơ chỉ phương của đường thẳng $\Delta$. Giá trị của $a + 2b$ bằng bao nhiêu (viết kết quả dưới dạng số thập phân)?

**Câu 2:** Hai quả bóng dạng hình cầu có kích thước khác nhau lần lượt đặt vào góc một căn nhà hình hộp chữ nhật sao cho quả bóng tiếp xúc với hai bức tường và nền của căn nhà đó. Trên bề mặt của mỗi quả bóng tồn tại một điểm có khoảng cách đến hai bức tường quả bóng tiếp xúc và đến nền nhà lần lượt là 2; 3; 1. Tính tổng độ dài các đường kính của hai quả cầu đó.

**Câu 3:** Một cuộc thi khoa học có 36 bộ câu hỏi, trong đó có 20 bộ câu hỏi về chủ đề tự nhiên và 16 bộ câu hỏi về chủ đề xã hội. Bạn An lấy ngẫu nhiên 1 bộ câu hỏi (lấy không hoàn lại), sau đó bạn Bình lấy ngẫu nhiên 1 bộ câu hỏi. Xác suất bạn Bình lấy được bộ câu hỏi về chủ đề xã hội bằng $\frac{a}{b}$ với $\frac{b}{a}$ là phân số tối giản. Giá trị $a + b$ bằng bao nhiêu?

**Câu 4:** Trong một đợt kiểm tra sức khỏe, có một loại bệnh X mà tỉ lệ người mắc bệnh là $0,2\%$ và một loại xét nghiệm Y mà ai mắc bệnh X khi xét nghiệm Y cũng có phản ứng dương tính. Tuy nhiên, có $0,6\%$ những người không bị bệnh X lại có phản ứng dương tính với xét nghiệm Y. Chọn ngẫu nhiên 1 người trong đợt kiểm tra sức khỏe đó. Giả sử người đó có phản ứng dương tính với xét nghiệm Y. Xác suất người đó mắc bệnh X là bao nhiêu (làm tròn kết quả đến hàng phần trăm)?

**Câu 5:** Một vật chuyển động trong 3 giờ với vận tốc $v(\text{km/h})$ phụ thuộc thời gian $t(h)$ có đồ thị là một phần của đường parabol có đỉnh $I(2;9)$ và trục đối xứng song song với trục tung như hình bên. Tính quãng đường $s$ mà vật di chuyển được trong 3 giờ đó theo đơn vị kilomet (làm tròn kết quả đến hàng phần mười).

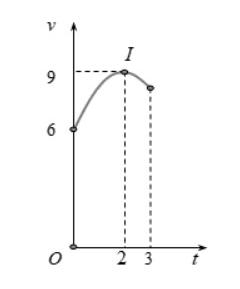
**Câu 6:** Một viên gạch hoa hình vuông cạnh 40cm. Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa (được tô đen như hình vẽ dưới). Tính diện tích mỗi cánh hoa của viên gạch theo đơn vị decimét vuông (làm tròn kết quả đến hàng phần trăm).

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh