PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1: Họ các nguyên hàm của hàm số $y = \cos x + x$ là

A. $\sin x + x^2 + C$.
B. $\sin x + \frac{1}{2}x^2 + C$.
C. $-\sin x + x^2 + C$.
D. $-\sin x + \frac{1}{2}x^2 + C$.

Câu 2: Họ nguyên hàm của hàm số $f(x) = e^x – 2x$ là

A. $e^x – x^2 + C$.
B. $\frac{1}{x+1}e^x – x^2 + C$.
C. $e^x + x^2 + C$.
D. $e^x – 2 + C$.

Câu 3: Nếu $\int_0^4 f(x)dx = 2$ và $\int_1^4 f(x)dx = 5$ thì $\int_0^1 f(x)dx$ bằng

A. $7$.
B. $3$.
C. $10$.
D. $-3$.

Câu 4: Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$. Biết hàm số $F(x)$ là một nguyên hàm của $f(x)$ trên $\mathbb{R}$ và $F(1) = 2$, $F(4) = 5$. Tích phân $\int_1^4 f(x)dx$ bằng

A. $3$.
B. $7$.
C. $6$.
D. $-3$.

Câu 5: Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường $y = x^3$, $y = 0$, $x = -1$ và $x = 1$ quanh trục $Ox$ bằng

A. $\frac{2}{7}\pi$.
B. $\pi$.
C. $\frac{6}{7}\pi$.
D. $2\pi$.

Câu 6: Vec-tơ nào sau đây là một vec-tơ pháp tuyến của mặt phẳng $-2x – y + 7z – 1 = 0$?

A. $\vec{n_1} = (2; 1; 7)$.
B. $\vec{n_2} = (2; -7; 1)$.
C. $\vec{n_3} = (2; 1; -7)$.
D. $\vec{n_4} = (2; -1; 7)$.

Câu 7: Trong không gian $Oxyz$, đường thẳng $\Delta$ đi qua điểm $A(-1; -1; 1)$ và nhận $\vec{u} = (1; 2; 3)$ làm vec-tơ chỉ phương có phương trình chính tắc là

A. $\frac{x-1}{-1} = \frac{y-2}{-1} = \frac{z-3}{1}$.
B. $\frac{x+1}{-1} = \frac{y+2}{-1} = \frac{z+3}{1}$.
C. $\frac{x+1}{1} = \frac{y+1}{2} = \frac{z-1}{3}$.
D. $\frac{x-1}{1} = \frac{y-1}{2} = \frac{z+1}{3}$.

Câu 9: Cho hai biến cố $A$ và $B$ có $P(B) = 0,8$ và $P(A|B) = 0,25$. Tính xác suất của biến cố $A$ giao $B$.

A. $0,1$.
B. $0,2$.
C. $0,25$.
D. $0,4$.

Câu 10: Cho hai biến cố $A$ và $B$. Xác suất của biến cố $B$ khi biến cố $A$ đã xảy ra được kí hiệu là

A. $P(A|B)$.
B. $P(B|A)$.
C. $P(AB)$.
D. $P(A \cup B)$.

Câu 11: Trong không gian $Oxyz$, cho mặt cầu $(S)$ có tâm $I(1; 2; -1)$ và bán kính bằng $2$. Phương trình của $(S)$ là

A. $(x+1)^2 + (y+2)^2 + (z-1)^2 = 2$.
B. $(x-1)^2 + (y-2)^2 + (z+1)^2 = 4$.
C. $(x+1)^2 + (y+2)^2 + (z-1)^2 = 4$.
D. $(x-1)^2 + (y-2)^2 + (z+1)^2 = 2$.

Câu 12: Trong không gian $Oxyz$, mặt cầu $(S): x^2 + y^2 + z^2 + 4x – 2y + 8z – 1 = 0$ có tọa độ tâm là

A. $(2; -1; 4)$.
B. $(2; -1; -4)$.
C. $(-2; 1; -4)$.
D. $(4; -2; 8)$.

PHẦN II. Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Trong không gian $Oxyz$, cho mặt phẳng $(P)$ có phương trình $x – 3y – 4z + 5 = 0$.

a) $(P)$ có một vec-tơ pháp tuyến là $\vec{n} = (1; -3; -4)$.

b) $(P)$ đi qua điểm $M(-1; 0; 1)$.

c) $(P)$ song song với đường thẳng $\Delta: \frac{x+2}{1} = \frac{y-1}{-1} = \frac{z}{1}$.

d) $(P)$ tiếp xúc với mặt cầu $(S): (x+6)^2 + (y-3)^2 + (z-4)^2 = 5^2$.

**Câu 2:** Trong không gian $Oxyz$, cho đường thẳng $\Delta: \begin{cases} x = 1 – 2t \\ y = -1 + t \\ z = -t \end{cases}$.

a) Một vec-tơ chỉ phương của đường thẳng $\Delta$ là $\vec{u} = (-2; 1; -1)$.

b) Phương trình mặt phẳng đi qua điểm $A(2; -3; 1)$ và vuông góc với $\Delta$ là $2x + y + z – 8 = 0$.

c) Điểm $P(1; -1; 0)$ thuộc đường thẳng $\Delta$.

d) Mặt phẳng $(P): x – 3y + 2z – 1 = 0$ song song với đường thẳng $\Delta$.

Câu 3: Một xe ô tô đang chạy với vận tốc $72$ $km/h$ thì người lái xe bất ngờ phát hiện chướng ngại vật trên đường cách đó $110m$. Người lái xe phanh ứng một giây, sau đó đạp phanh khẩn cấp. Kể từ thời điểm này, ô tô chuyển động chậm dần đều với tốc độ $v(t) = -20t + 40$ $(m/s)$, trong đó $t$ là thời gian tính bằng giây kể từ lúc đạp phanh. Gọi $s(t)$ là quãng đường xe ô tô đi được trong $t$ (giây) kể từ lúc đạp phanh.

a) Quãng đường $s(t)$ mà xe ô tô đi được trong thời gian $t$ (giây) là một nguyên hàm của hàm số $v(t)$.

b) $s(t) = -5t^2 + 20t$.

c) Thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là $2$ giây.

d) Xe ô tô đó va vào chướng ngại vật trên đường.

Câu 4: Một lô sản phẩm có 25 sản phẩm, trong đó có 8 sản phẩm chất lượng thấp. Lấy liên tiếp 2 sản phẩm trên, trong đó sản phẩm lấy ra ở lần thứ nhất không được bỏ lại vào lô sản phẩm.

Xét các biến cố A: “Lần thứ nhất lấy ra sản phẩm chất lượng thấp”. B: “Lần thứ hai lấy ra sản phẩm chất lượng thấp”.

a) Biến cố cả hai lần đều lấy ra sản phẩm chất lượng thấp là $A \cap B$.

b) $P(A) = \frac{8}{25}$.

c) $P(B|A) = \frac{7}{25}$.

d) Xác suất để cả hai sản phẩm lấy ra đều có chất lượng thấp là $\frac{7}{24}$.

PHẦN III. Câu trắc nghiệm trả lời ngắn.

Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: Trên bức tường cần trang trí một hình phẳng dạng parabol như hình vẽ bên dưới.

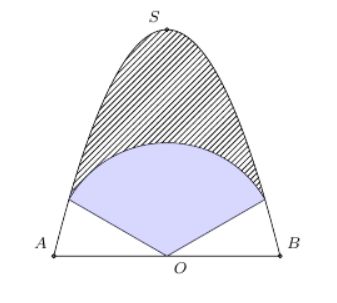
Biết $OS = AB = 4$ m, $O$ là trung điểm $AB$. Parabol trên được chia thành ba phần để sơn ba màu khác nhau với mức phí như sau: phần trên là phần kẻ sọc có giá $160.000$ đồng/m², phần giữa là hình quat tâm $O$, bán kính $2$ m được tô đậm có giá $200.000$ đồng/m², phần còn lại có giá $250.000$ đồng/m².

Tổng chi phí để sơn cả $3$ phần gần nhất với số tiền nào (làm tròn đến hàng triệu)?

Câu 2: Cho hai đường tròn $(O_1; 5)$ và $(O_2; 3)$ cắt nhau tại hai điểm $A$, $B$ sao cho $AB$ là một đường kính của đường tròn $(O_2; 3)$. Gọi $(D)$ là phần hình phẳng giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch sọc như hình vẽ). Quay $(D)$ quanh trục $OO_2$ ta được một khối tròn xoay. Tính thể tích $V$ của khối tròn xoay được tạo thành, làm tròn đến hàng phần chục.

Câu 3: Có hai hộp bóng bàn, các quả bóng bàn có kích thước và hình dạng như nhau. Hộp thứ nhất có 3 quả bóng bàn trắng và 3 quả bóng bàn màu vàng. Hộp thứ hai có 2 quả bóng bàn trắng và 4 quả bóng bàn màu vàng. Lấy ngẫu nhiên 4 quả bóng bàn ở hộp thứ nhất bỏ vào hộp thứ hai; rồi lấy ngẫu nhiên 1 quả bóng bàn ở hộp thứ hai. Tính xác suất để lấy được quả bóng màu vàng từ hộp thứ hai.

Câu 4: Một loại linh kiện do hai nhà máy I, II cùng sản xuất. Tỉ lệ phế phẩm của các nhà máy I, II lần lượt là $0,04$, $0,03$. Trong một lô linh kiện để lẫn lộn 80 sản phẩm của nhà máy I và 120 sản phẩm của nhà máy II. Một khách hàng lấy ngẫu nhiên một linh kiện từ lô hàng đó. Giả sử linh kiện được lấy ra là loại linh kiện phế phẩm. Hỏi xác suất linh kiện đó do nhà máy II sản xuất là bao nhiêu (làm tròn đến hàng phần trăm)?

Câu 5: Trong không gian $Oxyz$, một ngọn hải đăng có bóng đèn đặt tại tọa độ $O(0;0;0)$, đơn vị trên mỗi trục tính theo kilômet. Một tàu đi biển chuyển động hướng về ngọn hải đăng, đi qua hai vị trí $A(-500;-250;150), B(-200;-200;100)$. Khi tàu ở gần ngọn hải đăng nhất, tọa độ của vị trí tàu là $(a;b;c)$. Giá trị của biểu thức $-3a-b-c$ là bao nhiêu (làm tròn kết quả đến hàng đơn vị)?

Câu 6: Người ta muốn thiết kế một lều cắm trại có dạng là một phần mặt cầu bằng phần mềm 3D (như hình vẽ).

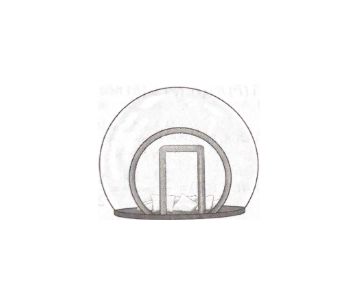
Cho biết phương trình bề mặt của lều là $(S): (x-3)^2 + (y-3)^2 + (z-1)^2 = 9$.

Phương trình mặt phẳng chứa cửa lều là $(P): x = 2$, tìm bán kính của đường tròn chứa cửa lều (làm tròn đến hàng phần trăm).

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh