4. Câu hỏi – Trả lời trắc nghiệm (03 điểm)

Câu 1. Họ tất cả các nguyên hàm của hàm số $f(x) = e^x – \frac{2}{x^2} + \sin x$ là

A. $\frac{e^x – 2}{x} + \cos x + C$.
B. $e^x – 2\ln x^2 – \cos x + C$.
C. $\frac{e^x + 2}{x} – \cos x + C$.
D. $\frac{e^x + 2}{x} + \cos x + C$.

Câu 2. Cho hàm số $y = f(x)$ như hình vẽ. Biết rằng $\int_{-2}^1 f(x)dx = a$ và $\int_1^2 f(x)dx = b$. Tìm diện tích $S$ của hình phẳng được tô đậm:

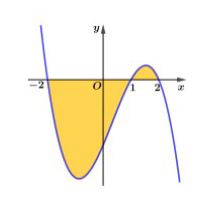
A. $S = -a – b$.
B. $S = a + b$.
C. $S = b – a$.
D. $S = a – b$.

Câu 3. Tính diện tích miền hình phẳng giới hạn bởi các đường $y = x^2 – 2x$, $y = 0$, $x = -10$, $x = 10$.

A. $S = \frac{2000}{3}$.
B. $S = 2008$.
C. $S = \frac{2008}{3}$.
D. $2000$.

Câu 4. Diện tích hình phẳng giới hạn bởi các đường $y = x^2$, $y = x + 2$ và hai đường thẳng $x = 0$, $x = 1$ là

A. $S = \frac{2}{9}$.
B. $S = \frac{9}{4}$.
C. $S = \frac{13}{6}$.
D. $S = \frac{8}{9}$.

Câu 5. Trong không gian $Oxyz$, cho vật thể nằm giữa hai mặt phẳng $x = 0$ và $x = 3$. Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục $Ox$ tại điểm có hoành độ $x$ $(0 \leq x \leq 3)$ là một hình vuông cạnh là $\sqrt{9 – x^2}$. Tính thể tích $V$ của vật thể.

A. $V = 18p$.
B. $V = 171$.
C. $V = 17Ip$.
D. $V = 18$.

Câu 6. Gieo con xúc xắc 1 lần. Gọi A là biến cố xuất hiện mặt 2 chấm. B là biến cố xuất hiện mặt chẵn. Xác suất $P(A|B)$ là

A. $\frac{1}{2}$.
B. $\frac{1}{3}$.
C. $\frac{2}{3}$.
D. $\frac{1}{6}$.

Câu 7. Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường $y = 10x^2, y = 0, x = 0, x = 1$ quay quanh trục hoành bằng:

A. $100p$.
B. $20p$.
C. $20$.
D. $2p$.

Câu 8. Trong không gian $Oxyz$, cho hai điểm $A(1; 3; -4)$, $B(-1; 1; 2)$. Mặt phẳng trung trực của đoạn thẳng $AB$ có phương trình là:

A. $x + y – 3z – 5 = 0$.
B. $-x – y + 3z + 2 = 0$.
C. $x + y – 3z + 10 = 0$.
D. $-2x – 2y + 6z – 11 = 0$.

Câu 9. Trong không gian $Oxyz$, hai mặt phẳng $(a): x + 2y + 3z + 4 = 0$ và $(b): x + 5y – z – 9 = 0$ có vị trí tương đối là

A. song song.
B. cắt nhau.
C. chéo nhau.
D. trùng nhau.

**Câu 10.** Trong không gian $Oxyz$, đường thẳng $d: \begin{cases} x = 1 – 2t \\ y = 3 + t \\ z = -2 \end{cases}$ có một vector chỉ phương là

A. $\vec{v} = (-2; 1; 0)$.
B. $\vec{v} = (-2; 1; -2)$.
C. $\vec{v} = (1; 3; -2)$.
D. $\vec{v} = (1; 3; 0)$.

Câu 12. Thư viện của một trường THPT có $60%$ tổng số sách là sách Văn học, $18%$ tổng số sách là sách tiểu thuyết và là sách Văn học. Chọn ngẫu nhiên một cuốn sách của thư viện. Tính xác suất để quyển sách được chọn là sách tiểu thuyết, biết rằng đó là quyển sách về Văn học.

A. $\frac{1}{10}$.
B. $\frac{3}{10}$.
C. $\frac{1}{2}$.
D. $\frac{3}{22}$.

5. Câu hỏi – Trả lời đúng sai (02 điểm)

Câu 13. Cho hàm số $f(x) = x^2 + 1$ và hàm số $g(x) = 2x$. Khi đó:

a) Họ nguyên hàm của hàm $g(x)$ là $G(x) = x^2 + c$

b) $\int_0^2 f(x)dx = \frac{14}{5}$

c) Diện tích hình phẳng giới hạn bởi hàm $f(x)$, $g(x)$ và hai đường thẳng $x = 0, x = 3$ bằng $3$

d) Cho hình phẳng $H$ giới hạn bởi hàm số $f(x) = x^2 + 1$, trục hoành và hai đường thẳng $x = 1, x = 2$. Thể tích khối tròn xoay tạo thành khi cho hình $H$ xoay quanh trục $Ox$ là $\frac{178p}{15}$

Câu 14. Trong không gian $Oxyz$, cho mặt phẳng $(P): 2x + 2y – z + 3 = 0$ và các điểm $A(1; 2; 3)$, $B(0; -1; 2)$, $C(1; 3; -2)$. Khi đó:

a) Điểm $A$ cách mặt phẳng $(P)$ một khoảng bằng $5$.

b) Mặt phẳng $(Q)$ đi qua điểm $B$ và song song với mặt phẳng $(P)$ có phương trình là $2x + 2y – z – 4 = 0$.

c) Đường thẳng đi qua điểm $A$ và vuông góc với mặt phẳng $(P)$ có phương trình tham số là $\begin{cases} x = 1 + 2t \ y = 2 + 2t \ z = 3 – t \end{cases}$

d) Gọi $H(a; b; c)$ là hình chiếu vuông góc của điểm $C$ lên mặt phẳng $(P)$. Khi đó giá trị của biểu thức $T = a – b + 9c = -4$.

6. Câu hỏi – Trả lời ngắn (02 điểm)

Câu 15. Số dân của một thị trấn sau $t$ năm kể từ năm 1990 được ước tính theo một hàm số theo thời gian $f(t)$ ($f(t)$ được tính bằng nghìn người). Biết rằng $f'(t) = \frac{34}{t^2 + 4t + 4}$ (nghìn người/năm) biểu thị tốc độ tăng dân số của thị trấn. Số dân của thị trấn đó vào năm 2035 là bao nhiêu nghìn người? (kết quả lấy chính xác đến hàng phần chục) biết dân số của thị trấn đó năm 1990 là $3$ nghìn người

Đáp án số: ______

Câu 16. Tung một đồng xu cân đối đồng chất 2 lần liên tiếp. Tính xác suất để cả hai lần đều xuất hiện mặt sấp biết rằng lần thứ nhất xuất hiện mặt sấp. Viết kết quả dưới dạng thập phân.

Đáp án số: ______

Câu 17. Hiệu suất của tim là lưu lượng máu được bơm bởi tim trên một đơn vị thời gian (lưu lượng máu chảy vào động mạch chủ). Để đo hiệu suất của tim, người ta bơm $A(mg)$ chất chỉ thị màu vào tâm nhĩ phải, chảy qua tim rồi vào động mạch chủ và đo nồng độ chất chỉ thị màu còn lại ở tim đến thời điểm $T(s)$ khi chất chỉ thị màu tan sạch. Gọi $c(t)$ là nồng độ $(mg/l)$ chất chỉ thị màu tại thời điểm $t(s)$ thì hiệu suất của tim được xác định $F = \frac{A}{\int_0^T c(t)dt}$ $(l/s)$ bởi. Tính hiệu suất của tim khi bơm 8 mg chất chỉ thị màu vào tâm nhĩ phải, biết $c(t) = \frac{1}{4}t(12 – t)$ với $0 \leq t \leq 12$ (kết quả làm tròn đến chữ số thập phân thứ hai).

(Nguồn: James Stewart, Calculus, Cengage Learning).

Đáp án số: ______

Câu 18. Trong không gian $Oxyz$ một cabin cáp treo được đặt xuất phát tại điểm $A(3; 4; 20)$ và chuyển động đều theo đường cáp có vec-tơ chỉ phương $\vec{u}(1; 2; 2)$ với tốc độ là $5m/s$ (đơn vị trên mỗi trục tọa độ là mét). Sau 30 giây đi chuyển cáp treo dừng lại tại điểm $M(a; b; c)$. Khi đó giá trị biểu thức $a + b + c$ là bao nhiêu?

Đáp án số: ______

7. Câu hỏi – Trả lời tự luận (03 điểm)

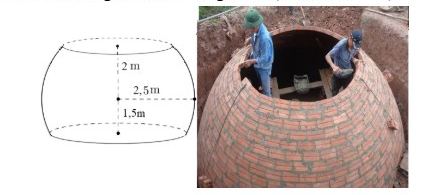
Câu 19. Mặt trong của một hầm biogas có hình dạng là một phần của mặt cầu đã cắt bỏ hai phần của nó bằng hai mặt phẳng song song với nhau (như hình vẽ). Bán kính của mặt cầu bằng $2,5m$. Mặt đáy phía dưới cách tâm một khoảng bằng $1,5m$. Mặt đáy phía trên cách tâm một khoảng bằng $2m$. Tính thể tích phần bên trong của hầm biogas đó (đơn vị là $m^3$)

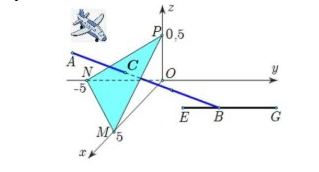
Câu 20. Một máy bay đang ở vị trí điểm $A(3,5; -2; 0,4)$ và sẽ hạ cánh ở vị trí điểm $B(3,5; 5; 0)$ trên đường băng $EG$ được mô hình hóa trong hệ trục tọa độ $Oxyz$ như hình vẽ bên dưới (đơn vị trên mỗi trục tọa độ là kilômét). Có một lớp mây được mô phỏng bởi một mặt phẳng $(\alpha)$ đi qua ba điểm $M(5; 0; 0)$, $N(0; -5; 0)$ và $P(0; 0; 0,5)$. Tìm tọa độ của điểm $C$ là vị trí mà máy bay xuyên qua đám mây để hạ cánh?

Câu 21. Trong một lô bóng đèn có $20%$ số bóng do phân xưởng I sản xuất. Số bóng còn lại do phân xưởng II sản xuất. Người ta nhận thấy có $2%$ số bóng trong lô hàng không đạt chất lượng. Biết rằng trong các bóng do phân xưởng I sản xuất, tỉ lệ bóng không đạt chất lượng là $1%$. Chọn ngẫu nhiên $1$ bóng đèn từ lô hàng. Biết rằng bóng được chọn không đạt chất lượng, tính xác suất bóng đó do phân xưởng II sản xuất.

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh