Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
A. Câu hỏi – Trả lời trắc nghiệm (03 điểm)
Câu 1. Tìm họ nguyên hàm của hàm số $f(x) = x^{2024}$.
A. $\int f(x)dx = \frac{1}{2023}x^{2023} + C$.
B. $\int f(x)dx = 2024.x^{2023} + C$.
C. $\int f(x)dx = \frac{1}{2025}x^{2025} + C$.
D. $\int f(x)dx = x^{2025} + C$.
Câu 2. Trong không gian $Oxyz$, cho mặt cầu $(S): (x – 3)^2 + y^2 + (z – 2)^2 = 16$. Bán kính của $(S)$ bằng
A. $8$.
B. $32$.
C. $16$.
D. $4$.
Câu 3. Từ một hộp có 4 tấm thẻ cùng loại được ghi số lần lượt từ 1 đến 4. Bạn An lấy ra một cách ngẫu nhiên một thẻ từ hộp, bỏ thẻ đó ra ngoài và lại lấy một cách ngẫu nhiên thêm một thẻ nữa. Xét biến cố $A$ là “thẻ lấy ra lần thứ nhất ghi số 3”. Số các kết quả thuận lợi của biến cố $A$ là
A. $3$.
B. $2$.
C. $4$.
D. $1$.
Câu 4. Trong không gian $Oxyz$, cho mặt phẳng $(P): \frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1$. Khoảng cách từ gốc tọa độ $O$ đến mặt phẳng $(P)$ bằng
A. $6$.
B. $\frac{11}{6}$.
C. $1$.
D. $\frac{6}{7}$.
Câu 5. Cho $\int_1^2 [4f(x) – 2x]dx = 1$. Khi đó $\int_1^2 f(x)dx$ bằng
A. $-1$.
B. $1$.
C. $-3$.
D. $3$.
Câu 6. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = e^x$, trục hoành và hai đường thẳng $x = 0$ và $x = 3$.
A. $e^3$.
B. $e^3 – 1$.
C. $e^3 – 1$.
D. $e(e^2 – 1)$.
Câu 7. Trong không gian $Oxyz$. Phương trình nào sau đây là phương trình mặt cầu $(S)$ tâm $A(2; 1; 0)$, đi qua điểm $B(0; 1; 2)$?
A. $(S): (x + 2)^2 + (y + 1)^2 + z^2 = 8$.
B. $(S): (x – 2)^2 + (y – 1)^2 + z^2 = 8$.
C. $(S): (x + 2)^2 + (y + 1)^2 + z^2 = 64$.
D. $(S): (x + 2)^2 + (y + 1)^2 + z^2 = 64$.
Câu 8. Cho hai biến độc lập $A, B$ với $P(A) = 0,8; P(B) = 0,3$. Khi đó, $P(A|B)$ bằng
A. $0,8$.
B. $0,3$.
C. $0,4$.
D. $0,6$.
Câu 9. Trong không gian $Oxyz$, cho mặt phẳng $(P): 2x + 4y + 3z – 5 = 0$ và mặt phẳng $(Q): -4x – 8y – 6z + 2 = 0$. Vị trí tương đối của hai mặt phẳng $(P)$ và $(Q)$ là
A. Mặt phẳng $(P)$ vuông góc với mặt phẳng $(Q)$.
B. Mặt phẳng $(P)$ song song với mặt phẳng $(Q)$.
C. Mặt phẳng $(P)$ cắt và không vuông góc với mặt phẳng $(Q)$.
D. Mặt phẳng $(P)$ trùng với mặt phẳng $(Q)$.
Câu 10. Cho hình phẳng $D$ giới hạn bởi đồ thị hàm số $y = \sqrt{5 – x}, x \leq 5$, trục tung, trục hoành. Thể tích khối tròn xoay tạo thành khi quay $D$ quanh trục $Ox$ là
A. $\frac{25p}{2}$.
B. $\frac{25}{2}$.
C. $25p$.
D. $\frac{25}{4}$.
Câu 11. Một hộp chứa 8 bi xanh, 2 bi đỏ. Lần lượt bốc từng bi. Giả sử lần đầu tiên bốc được bi xanh. Xác định xác suất lần thứ 2 bốc được bi đỏ.
A. $\frac{1}{10}$.
B. $\frac{2}{9}$.
C. $\frac{8}{9}$.
D. $\frac{2}{5}$.
Câu 12. Trong không gian $Oxyz$, cho điểm $A(1; -2; 3)$, $B(-1; 1; 2)$. Tập hợp $M(x; y; z)$ sao cho $MA = \sqrt{2}MB$ là một mặt cầu có bán kính bằng
A. $\sqrt{7}$.
B. $4\sqrt{7}$.
C. $2\sqrt{7}$.
D. $\sqrt{14}$.
B. Câu hỏi – Trả lời đúng/sai (02 điểm)
Câu 13. Một chất điểm bắt đầu chuyển động thẳng đều với vận tốc $v_0$, sau $4$ giây chuyển động thì gặp chướng ngại vật nên bắt đầu giảm tốc độ với vận tốc chuyển động $v(t) = -\frac{5}{2}t + a$ (m/s), $(t \geq 4)$ cho đến khi dừng hẳn. Quãng đường chất điểm đi được kể từ lúc chuyển động đến khi dừng hẳn là $80m$. Khi đó:
a) Quãng đường chất điểm đi chuyển được sau $4$ (giây) bằng: $S(4) = 4v_0$ (m)
b) Quãng đường chất điểm đi chuyển được sau $5$ (giây) bằng: $S(5) = \int_0^5 v(t)dt$ (m)
c) $v_0 < 8$ (m/s)
d) Vận tốc trung bình $v_{tb}$ của chất điểm trong khoảng thời gian từ $3$ giây đến $7$ giây kể từ lúc bắt đầu thỏa mãn $v_{tb} < 8$ (m/s)
Câu 14. Trong không gian $Oxyz$, cho hai điểm $A(2; 4; 1)$, $B(-2; 2; -3)$. Gọi $I$ là tâm mặt cầu $(S)$ có đường kính $AB$. Khi đó:
a) $I(0; 3; -1)$, $R = 6$.
b) Phương trình mặt phẳng tiếp xúc mặt cầu tại A là $(P): 2x + y + 2z – 10 = 0$.
c) Bán kính đường tròn giao tuyến của mặt cầu với $(Q): 2x – y + 2z – 1 = 0$ là $5$.
d) Gọi $I’$ là tâm mặt cầu $(S’)$ sao cho diện tích mặt cầu $(S)$ gấp $4$ lần diện tích mặt cầu $(S’)$. Khi đó, $II’ = \frac{11}{2}$.
C. Câu hỏi – Trả lời ngắn (02 điểm)
Câu 15. Một lô các sản phẩm do hai nhà máy sản xuất, biết rằng số sản phẩm của nhà máy thứ nhất gấp ba lần số sản phẩm của nhà máy thứ hai. Tỉ lệ sản phẩm tốt của nhà máy thứ nhất là $0,8$ và nhà máy thứ hai là $0,7$. Lấy ngẫu nhiên ra một sản phẩm. Tính xác suất để sản phẩm lấy ra là tốt. làm tròn kết quả đến hàng phần trăm.
Đáp án số: ______
Câu 16. Bạn An có các tấm thẻ hình chữ nhật có kích thước khác nhau nhưng có cùng chu vi là $6cm$. Trên mỗi tấm thẻ An vẽ một hình parabol sao cho đỉnh của parabol trùng với trung điểm một cạnh của tấm thẻ như hình vẽ. Hỏi diện tích của hình parabol lớn nhất mà An vẽ được bằng bao nhiêu xăng tí mét vuông?
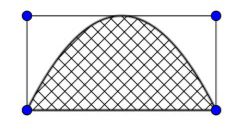
Đáp án số: ______
Câu 17. Khi cắt vật thể bởi mặt phẳng vuông góc với trục $Ox$ tại điểm có hoành độ là $x$ $(0 \leq x \leq 3)$, ta được mặt cắt là một hình vuông có cạnh là $\sqrt{9 – x^2}$ (xem hình). Tính thể tích của vật thể đã cho.

Đáp án số: ______
Câu 18. Trong không gian $Oxyz$, cho điểm $A(-2; 2; -2), B(3; -3; 3)$. $M$ là điểm thay đổi trong không gian thỏa mãn $\frac{MA}{MB} = \frac{2}{3}$. Khi đó độ dài $OM$ lớn nhất bằng? Làm tròn kết quả đến hàng phần mười.
Đáp án số: ______
D. Câu hỏi – Trả lời tự luận (03 điểm)
Câu 19. Bạn Minh làm hai bài tập kế tiếp. Xác suất Minh làm đúng bài thứ nhất là 0,7. Nếu Minh làm đúng bài thứ nhất thì khả năng làm đúng bài thứ hai là 0,8 nhưng nếu Minh làm sai bài thứ nhất thì khả năng làm đúng bài thứ hai là 0,2. Tính xác suất để Minh làm đúng bài thứ nhất biết rằng Minh làm đúng bài thứ hai.
Câu 20. Tính diện tích hình phẳng $(H)$ giới hạn bởi các đồ thị hàm số $y = 2^x; y = \frac{2}{\sqrt{x}}; x = \frac{1}{2}; x = 4$
Câu 21. Trong hệ tọa độ $Oxyz$, cho điểm $A(2; 1; 3)$, mặt phẳng $(P): 2x + 2y – z – 3 = 0$ và mặt cầu $(S): x^2 + y^2 + z^2 – 6x – 4y – 10z + 2 = 0$. Gọi $D$ là đường thẳng đi qua $A$, nằm trong mặt phẳng $(P)$ và cắt $(S)$ tại hai điểm $M, N$. Độ dài đoạn $MN$ nhỏ nhất bằng bao nhiêu?

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh

