Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
A. Câu hỏi – Trả lời trắc nghiệm (03 điểm)
Câu 1. Gọi $S$ là diện tích hình thang cong giới hạn bởi đồ thị hàm số $y = f(x) = e^x$, trục hoành, và đường thẳng $x = 1$ (như hình vẽ dưới). Khi đó $S$ được tính bằng công thức:
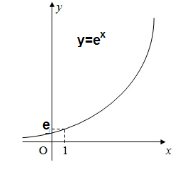
A. $S = \int_0^1 (e^x – x)dx$.
B. $S = \int_0^1 e^x dx$.
C. $S = \int_0^e (x – 1)dx$.
D. $S = \int_0^1 (e^x – 1)dx$.
Câu 2. Trong không gian $Oxyz$, tính khoảng cách giữa hai mặt phẳng song song $(P): x + 3y – 2z + 4 = 0$ và $(Q): 6x + 18y – 12z = 0$?
A. $d((P); (Q)) = \frac{\sqrt{7}}{14}$.
B. $d((P); (Q)) = \frac{2\sqrt{14}}{7}$.
C. $d((P); (Q)) = \frac{2\sqrt{7}}{14}$.
D. $d((P); (Q)) = \frac{\sqrt{14}}{7}$.
Câu 3. Kí hiệu $h(x)$ là chiều cao của một cây (tính theo mét) sau khi trồng $x$ năm. Biết rằng sau năm đầu tiên cây cao $2m$. Trong $10$ năm tiếp theo, cây phát triển với tốc độ $h'(x) = \frac{1}{x}$. Xác định chiều cao $h(x)$ của cây sau $x$ năm $(1 \leq x \leq 11)$.
A. $h(x) = \ln x – 2$.
B. $h(x) = \ln x + 2$.
C. $h(x) = \ln x + 1$.
D. $h(x) = \ln x – 1$.
Câu 4. Trong không gian $Oxyz$, cho hai mặt phẳng $(P): 2x + y – z – 1 = 0$, $(Q): x – 2y + z – 5 = 0$. Khi đó giao tuyến của hai mặt phẳng $(P)$ và $(Q)$ có một vector chỉ phương là
A. $\vec{u} = (1; -2; 1)$.
B. $\vec{u} = (2; 1; -1)$.
C. $\vec{u} = (1; 3; 5)$.
D. $\vec{u} = (-1; 3; -5)$.
Câu 5. Tìm $F(x) = \int p^3 dx$.
A. $F(x) = p^3 x + C$.
B. $F(x) = \frac{p^3 x^2}{2} + C$.
C. $F(x) = 2px + C$.
D. $F(x) = \frac{p^3}{3} + C$.
Câu 6. Trong không gian $Oxyz$, cho mặt cầu $(S): (x – 2)^2 + (y + 1)^2 + (z – 1)^2 = 9$. Tìm tọa độ tâm $I$ và bán kính $R$ của mặt cầu $(S)$
A. $I(-2; 1; -1), R = 3$.
B. $I(-2; 1; -1), R = 9$.
C. $I(2; -1; 1), R = 3$.
D. $I(2; -1; 1), R = 9$.
Câu 7. Viết công thức tính thể tích $V$ của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục $Ox$ tại các điểm $x = a$, $x = b$ $(a < b)$, có thiết diện bị cắt bởi mặt phẳng vuông góc với trục $Ox$ tại điểm có hoành độ $x$ $(a \leq x \leq b)$ là $S(x)$.
A. $V = p^2 \int_a^b |S(x)|dx$.
B. $V = \int_a^b S(x)dx$.
C. $V = p \int_a^b S(x)dx$.
D. $V = p \int_a^b S^2(x)dx$.
Câu 8. Trong không gian $Oxyz$, cho hai điểm $A(4; 0; 1)$ và $B(-2; 2; 3)$. Mặt phẳng trung trực của đoạn thẳng $AB$ có phương trình là
A. $x + y + 2z – 1 = 0$.
B. $x + y + 2z = 0$.
C. $3x – y – z = 0$.
D. $6x – 2y – 2z + 1 = 0$.
Câu 9. Cho hai biến cố xung khắc $A$ và $B$ với $P(A) = 0,2$, $P(B) = 0,4$. Khi đó $P(A|B)$ bằng
A. $0,5$.
B. $0,2$.
C. $0,4$.
D. $0$.
Câu 10. Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số $y = 2^x$, $y = -x + 6$ và hai đường thẳng $x = 0$, $x = 2$ bằng
A. $10 + \frac{3}{\ln 2}$.
B. $10 – \frac{3}{\ln 2}$.
C. $10 – \frac{4}{\ln 2}$.
D. $10 + \frac{4}{\ln 2}$.
Câu 11. Trong không gian $Oxyz$, cho mặt cầu $(S): (x – 1)^2 + (y + 2)^2 + (z – 3)^2 = 4$. Diện tích của mặt cầu $(S)$ là
A. $p$.
B. $4p$.
C. $16p$.
D. $\frac{32}{3}p$.
Câu 12. Trong kì kiểm tra môn Toán của một trường trung học phổ thông có 200 học sinh tham gia, trong đó có 95 học sinh nam và 105 học sinh nữ. Khi công bố kết quả của kì kiểm tra đó, có 50 học sinh đạt điểm giỏi, trong đó có 24 học sinh nam và 26 học sinh nữ. Chọn ngẫu nhiên một học sinh trong số 200 học sinh đó. Tính xác suất để học sinh được chọn ra đạt điểm giỏi, biết rằng học sinh đó là nữ (làm tròn kết quả đến hàng phần trăm) là
A. $0,25$.
B. $0,24$.
C. $0,22$.
D. $0,23$.
B. Câu hỏi – Trả lời đúng/sai (02 điểm)
Câu 13. Trong không gian $Oxyz$, cho các điểm $A(1; 1; 1); B(1; 2; 3); C(4; 1; 2)$. Khi đó:
a) Phương trình mặt phẳng $(ABC)$ là $x + 6y – 3z + 4 = 0$.
b) Điểm $D(1; -1; 0)$ cũng thuộc mặt phẳng $(ABC)$.
c) $\overrightarrow{AB} = (0; 1; 2); \overrightarrow{AC} = (3; 0; 1)$
d) Một vector pháp tuyến của mặt phẳng $(ABC)$ là $\vec{n} = (1; 6; -3)$.
Câu 14. Cho đồ thị hàm số $y = x^3 – 2x^2 – 3x + 4$ $(C)$ và đường thẳng $d: y = 2x – 2$. Khi đó:
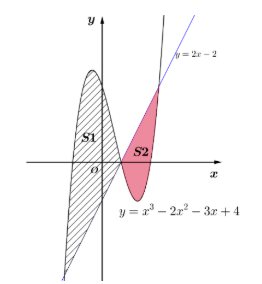
a) Đường thẳng $d$ cắt đồ thị $(C)$ tại ba điểm $A(-2; -6), B(1; 0), C(3; 4)$.
b) Diện tích hình phẳng giới hạn bởi đồ thị $(C)$, trục hoành, đường thẳng $x = -1, x = 2$ bằng $\frac{21}{4}$.
c) Diện tích hình phẳng giới hạn bởi đồ thị $(C)$ và đường thẳng $d$ bằng $\frac{253}{12}$.
d) Biết đường thẳng $d$ cắt đồ thị $(C)$ thành hai miền $S_1$ và $S_2$. Tỉ số $\frac{S_1}{S_2} = \frac{63}{16}$.
C. Câu hỏi – Trả lời ngắn (02 điểm)
Câu 15. Tìm giá trị của $a$ để $F(x) = \frac{ax + 3}{x – 4}$ là một nguyên hàm của hàm số $f(x) = \frac{1}{(x – 4)^2}$
Đáp án số: ______
Câu 16. Trong không gian $Oxyz$, một ngôi nhà như hình vẽ dưới đây có sàn nhà nằm trên mặt phẳng $(Oxy)$. Hai mái nhà lần lượt nằm trên các mặt phẳng $(P): x – 2y + 5 = 0$ và $(Q): x – 2y – 3z + 20 = 0$. Hỏi là chiều cao của ngôi nhà tính từ sàn nhà lên nóc nhà là bao nhiêu? (làm tròn đến hàng đơn vị)

Đáp án số: ______
Câu 17. Một chiếc lều mái vòm có hình dạng như hình bên. Nếu cắt lều bằng mặt phẳng song song với mặt đáy và cách mặt đáy một khoảng $x$ (mét) $(0 \leq x \leq 3)$ thì được hình chữ nhật có các kích thước lần lượt là $x$ và $\sqrt{9 – x^2}$. Tính thể tích cái lều (đơn vị $m^3$).
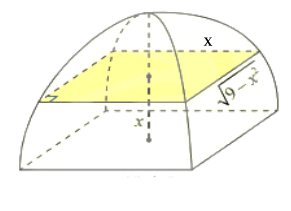
Đáp án số: ______
Câu 18. Mực nước trong hồ chứa của nhà máy điện thủy triều thay đổi trong suốt một ngày do nước chảy ra (khi thủy triều xuống) và nước chảy vào (khi thủy triều lên). Gọi $h(t)$ là mực nước trong hồ tại thời điểm $t$ giờ. Tốc độ thay đổi của mực nước trong hồ chứa được cho bởi hàm số $h'(t) = \frac{1}{216}(5t^2 – 120t + 480)$, trong đó $t$ tính bằng giờ $(0 \leq t \leq 24)$, $h'(t)$ tính bằng mét/giờ. Biết rằng tại thời điểm $t = 0$ (giờ), mực nước trong hồ chứa là 6m. Tính mực nước trong hồ tại thời điểm $t = 7$ (giờ). (Làm tròn kết quả đến hàng phần chục)
Đáp án số: ______
D. Câu hỏi – Trả lời tự luận (03 điểm)
Câu 19. Thống kê 2000 sinh viên một khóa của trường đại học theo giới tính và ngành học thu được các số liệu sau
| Nam | Nữ | |
| Học tại chính ngân hàng | 400 | 500 |
| Học ngành trí kinh doanh | 800 | 300 |
Lấy ngẫu nhiên một sinh viên khóa đó. Nếu đã chọn được một sinh viên nam hãy tính xác suất để người đó học tại chính ngân hàng bằng bao nhiêu?
Câu 20. Cho tam giác $ABC$ với tọa độ các điểm $A(0; 0)$, $B(2; 4)$ và $C(4; 0)$. Thể tích hình tròn xoay khi quay tam giác $ABC$ quanh trục $Ox$ bằng bao nhiêu?
Câu 21. Cho các đường thẳng $d_1: \frac{x-1}{1} = \frac{y+1}{2} = \frac{z}{-1}$ và đường thẳng $d_2: \frac{x-2}{1} = \frac{y}{2} = \frac{z+3}{2}$. Gọi $\Delta$ là đường thẳng đi qua $A(1; 0; 2)$, cắt $d_1$ và vuông góc với $d_2$. Tính khoảng cách từ gốc tọa độ $O$ tới đường thẳng $\Delta$.

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh

