Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
A. Câu hỏi – Trả lời trắc nghiệm (03 điểm)
Câu 1. Cho $f(x)$ là hàm số liên tục trên đoạn $[1; 2]$. Biết $F(x)$ là một nguyên hàm của hàm số $f(x)$ trên đoạn $[1; 2]$ thỏa mãn $F(1) = -2$ và $F(2) = 3$. Khi đó $\int_1^2 f(x)dx$ bằng:
A. $5$.
B. $1$.
C. $-5$.
D. $-1$.
Câu 2. Trong không gian $Oxyz$, cho mặt phẳng $(a): y – z + 3 = 0$. Vec-tơ nào dưới đây là vec-tơ pháp tuyến của mặt phẳng (a)?
A. $\vec{n} = (1; -1; 3)$.
B. $\vec{n} = (0; 1; -1)$.
C. $\vec{n} = (0; 1; 1)$.
D. $\vec{n} = (1; -1; 0)$.
Câu 3. Cho $\int_0^1 f(x)dx = 3$ và $\int_0^1 g(x)dx = 7$. Tính $\int_0^1 [f(x) – g(x)]dx$.
A. $10$.
B. $-4$.
C. $-10$.
D. $4$.
Câu 4. Trong không gian $Oxyz$, mặt phẳng nào đi qua gốc tọa độ
A. $2x – 3y + 5z = 0$.
B. $2x – 3z + 1 = 0$.
C. $3x – 10 = 0$.
D. $3x – z + 2 = 0$.
Câu 5. Trong một nhóm 25 người, có 15 người thích uống trà, 17 người thích uống cà phê, 9 người thích uống cả cà phê và trà. Chọn ngẫu nhiên một người trong nhóm. Biết rằng, người đó thích uống cà phê. Xác suất để người đó thích uống trà là
A. $\frac{9}{17}$.
B. $\frac{8}{17}$.
C. $\frac{9}{19}$.
D. $\frac{10}{19}$.
Câu 6. Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = x^3 – 4x$, trục hoành và hai đường thẳng $x = 0$; $x = 3$ bằng
A. $p\int_0^3 |x^3 – 4x|dx$.
B. $\int_0^3 |x^3 – 4x|dx$.
C. $p\int_0^3 (x^3 – 4x)^2 dx$.
D. $\int_0^3 (x^3 – 4x)dx$.
Câu 7. Gieo hai con xúc sắc giống nhau. Tính xác suất để ta có tổng số chấm thu được bằng $6$, biết rằng tổng đó là một số chẵn.
A. $\frac{1}{6}$.
B. $\frac{5}{36}$.
C. $\frac{1}{3}$.
D. $\frac{5}{18}$.
Câu 8. Trong không gian $Oxyz$, mặt phẳng $(a)$ đi qua điểm $A(2; -1; 4)$ và song song với mặt phẳng $(Oxy)$ có phương trình là:
A. $x – 2 = 0$.
B. $y + 1 = 0$.
C. $z – 4 = 0$.
D. $x – y – 1 = 0$.
Câu 9. Diện tích của hình phẳng giới hạn bởi các đường $y = e^x$, $y = x^2 – 1$, $x = -1, x = 1$ (tham khảo hình vẽ) bằng
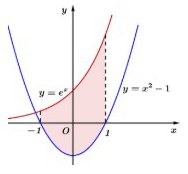
A. $\frac{3e^2 + 4e – 3}{3e}$.
B. $\frac{3e^2 + 4e – 3}{e}$.
C. $\frac{3e^2 + 4e + 3}{3e}$.
D. $\frac{3e^2 – 4e + 3}{3e}$.
Câu 10. Trong không gian $Oxyz$, cho điểm $I(3; 1; 5)$. Viết phương trình mặt cầu $(S)$ tâm $I$ và có bán kính $R = 3$.
A. $(S): (x – 3)^2 + (y – 1)^2 + (z – 5)^2 = 9$.
B. $(S): (x – 3)^2 + (y – 1)^2 + (z – 5)^2 = 3$.
C. $(S): (x + 3)^2 + (y + 1)^2 + (z + 5)^2 = 9$.
D. $(S): (x + 3)^2 + (y + 1)^2 + (z + 5)^2 = 3$.
**Câu 11.** Trong không gian $Oxyz$, tọa độ giao điểm của hai đường thẳng $d: \begin{cases} x = -3 + 2t \\ y = -2 + 3t \\ z = 6 + 4t \end{cases}$ và $d’: \begin{cases} x = 5 + t’ \\ y = -1 – 4t’ \\ z = 20 + t’ \end{cases}$ là
A. $(8; -13; 23)$.
B. $(0; -3; 2)$.
C. $(-7; -8; -2)$.
D. $(3; 7; 18)$.
Câu 12. Rút từ bộ bài tú lơ kho 52 con lần lượt ra hai con bài theo phương thức không hoàn lại. Tính xác suất để con thứ hai là Át, biết con thứ nhất đã là Át.
A. $\frac{1}{17}$.
B. $\frac{1}{13}$.
C. $\frac{3}{52}$.
D. $\frac{4}{51}$.
B. Câu hỏi – Trả lời đúng/sai (02 điểm)
Câu 13. Trong không gian $Oxyz$, biết $x^2 + y^2 + z^2 + 4mx + 2my – 2mz + 9m^2 – 27 = 0$ là phương trình mặt cầu và $m$ là tham số. Khi đó:
a) Có $5$ giá trị nguyên $m$ để phương trình đã cho là phương trình mặt cầu
b) Với $m = 0$, bán kính của mặt cầu là $\sqrt{33}$
c) Với $m < 0$, thì khoảng cách của mặt cầu và $I\left(-3; 1; \frac{3}{2}\right)$ $(P): -2x + 2y – z + 15 = 0$ là $1$
d) Gọi $A$ và $B$ là $2$ tâm mặt cầu sao cho thể tích của hình cầu là $36p$. Trung điểm của $AB$ là $\left(4\sqrt{6}; 2\sqrt{6}; -2\sqrt{6}\right)$
C. Câu hỏi – Trả lời ngắn (02 điểm)
Câu 15. Gia đình ông Bình xây một cái chòi hình bát giác, trong đó mái chòi $(H)$ có dạng hình “chóp bát giác cong đều” có trần bằng gỗ như hình vẽ bên. Đáy của $(H)$ là một hình bát giác đều có cạnh là $a = \frac{3\sqrt{2\sqrt{2} + 2}}{\sqrt{2} + 2}$ (m). Chiều cao $SO = 6m$ ($SO$ vuông góc với mặt phẳng đáy). Các cạnh bên của $(H)$ là các sợi dây thép $d_1; d_2; d_3; d_4; d_5; d_6; d_7; d_8$ nằm trên các đường parabol có trục đối xứng song song với $SO$. Giả sử giao tuyến (nếu có) của $(H)$ với mặt phẳng $(α)$ vuông góc với $SO$ là một bát giác đều và khi $(α)$ khi qua trung điểm của $SO$ thì bát giác đều có cạnh $b = \frac{\sqrt{2\sqrt{2} + 2}}{\sqrt{2} + 2}$ (m). Tính thể tích phần không gian nằm bên trong mái chòi $(H)$ đó. Đơn vị tính: $m^3$, làm tròn kết quả đến hàng đơn vị.

Đáp án số: ______
Câu 16. Trong không gian $Oxyz$, cho điểm $M(0; -1; 2)$ và hai đường thẳng $d_1: \frac{x-1}{1} = \frac{y+2}{-1} = \frac{z-3}{2}$, $d_2: \frac{x+1}{2} = \frac{y-4}{-1} = \frac{z-2}{4}$. Phương trình đường thẳng đi qua $M$, cắt cả $d_1$ và $d_2$ có một vector chỉ phương là $(9; a; b)$. Biết $x = a$ và $x = b$ là hai nghiệm của phương trình $x^2 – mx + n = 0$. Tính $m^2 – n + 1$.
Đáp án số: ______
Câu 17. Một công ty được phân giới thiệu một dụng cụ kiểm tra sớm bệnh sốt xuất huyết. Về kiểm định chất lượng sản phẩm, họ cho biết như sau: Số người được thử là 9000, trong số đó có 1500 người đã nhiễm bệnh sốt xuất huyết và có 7500 người không nhiễm bệnh sốt xuất huyết. Khi thử bằng dụng cụ kiểm tra sớm, trong 1500 người đã nhiễm bệnh sốt xuất huyết, có 76% số người đó cho kết quả dương tính, còn lại cho kết quả âm tính. Mặt khác, trong 7500 người không bị nhiễm bệnh sốt xuất huyết, có 7% số người đó cho kết quả dương tính, còn lại cho kết quả âm tính khi kiểm tra. Chọn ngẫu nhiên một người trong số những người thử nghiệm. Tính xác suất để người được chọn ra bị nhiễm bệnh sốt xuất huyết, biết rằng người đó có kết quả thử nghiệm âm tính (Làm tròn kết quả đến hàng phần trăm).
Đáp án số: ______
Câu 18. Trong không gian $Oxyz$, $D$ là đường thẳng đi qua điểm $A(1; -1; 2)$, vuông góc với đường thẳng $d_1: \frac{x-1}{2} = \frac{y+1}{-1} = \frac{z-4}{-1}$, đồng thời tạo với đường thẳng $d_2: \frac{x+1}{1} = \frac{y-1}{-2} = \frac{z}{2}$ một góc lớn nhất. Biết phương trình đường thẳng $D$ có dạng $\frac{x-1}{4} = \frac{y+1}{a} = \frac{z-2}{b}$. Tính $a^2 + b^2$.
Đáp án số: ______
D. Câu hỏi – Trả lời tự luận (03 điểm)
Câu 19. Trên mặt phẳng tọa độ $Oxy$ vẽ nửa đường tròn tâm $O$, bán kính $r = 2$ nằm phía trên trục $Ox$. Gọi $D$ là hình phẳng giới hạn bởi nửa đường tròn, trục $Ox$ và đường thẳng $x = 1$ (hình vẽ). Tính thể tích khối tròn xoay được tạo thành khi quay $D$ quanh trục $Ox$.
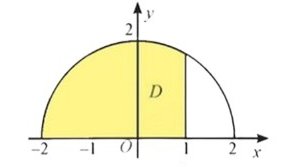
Câu 20. Khảo sát 100 người trong đó có 49 nam và 51 nữ về việc có nuôi thú cưng không thi được bảng sau
| Có thú cưng | Không có thú cưng | |
|---|---|---|
| Nam | 41 | 8 |
| Nữ | 45 | 6 |
| Tổng | 86 | 14 |
Chọn ngẫu nhiên một người trong số người được khảo sát. Biết người đó là nam, tính xác suất của biến cố người được chọn nuôi thú cưng?
**Câu 21.** Trong không gian $Oxyz$, cho đường thẳng $d: \begin{cases} x = 1 + t \\ y = 2t \\ z = -1 \end{cases}$, điểm $M(1; 2; 1)$ và mặt phẳng $(P): 2x + y – 2z – 1 = 0$. Viết phương trình đường thẳng $\Delta$ đi qua $M$, song song với $(P)$ và vuông góc với $d$.

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh

