Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
A. Câu hỏi – Trả lời trắc nghiệm (03 điểm)
Câu 1. Mặt cầu tâm $I(1; -2; 3)$ và tiếp xúc với mặt phẳng $(P): 2x – y + 2z – 1 = 0$ có phương trình là
A. $(x – 1)^2 + (y + 2)^2 + (z – 3)^2 = 3$.
B. $(x – 1)^2 + (y – 2)^2 + (z – 3)^2 = 9$.
C. $(x – 1)^2 + (y + 2)^2 + (z – 3)^2 = 9$.
D. $(x – 1)^2 + (y – 2)^2 + (z – 3)^2 = 3$.
Câu 2. Gọi $S$ là diện tích của hình phẳng giới hạn bởi các đường $y = 2^x$, $y = 0$, $x = 0$ và $x = 2$. Mệnh đề nào dưới đây đúng?
A. $S = p\int_0^2 2^x dx$.
B. $S = \int_0^2 2^x dx$.
C. $S = p\int_0^2 2^{2x} dx$.
D. $S = \int_0^2 2^{2x} dx$.
**Câu 3.** Một vector chỉ phương của đường thẳng $\begin{cases} x = 2 + t \\ y = -1 + 3t, t \in \mathbb{R} \\ z = 2t \end{cases}$ là
A. $\vec{u_1} = (1; 3; 0)$.
B. $\vec{u_2} = (2; -1; 2)$.
C. $\vec{u_1} = (1; 3; 2)$.
D. $\vec{u_2} = (2; -1; 0)$.
Câu 4. Trong không gian $Oxyz$, cho mặt phẳng cho mặt phẳng $(P)$ có phương trình $3x + 4y + 2z + 4 = 0$ và điểm $A(1; -2; 3)$. Tính khoảng cách $d$ từ $A$ đến $(P)$.
A. $d = \frac{5}{29}$.
B. $d = \frac{5}{\sqrt{29}}$.
C. $d = \frac{\sqrt{5}}{3}$.
D. $d = \frac{5}{9}$.
Câu 5. Trong không gian $Oxyz$, mặt phẳng đi qua gốc tọa độ và song song với mặt phẳng $5x – 3y + 2z – 3 = 0$ có phương trình là
A. $5x – 3y + 2z + 5 = 0$.
B. $5x – 3y + 2z = 0$.
C. $10x + 6y + 4z = 0$.
D. $4x + y + 5z = 0$.
Câu 6. Cho hai biến cố độc lập $A$ và $B$ với $P(A) = 0,8; P(B) = 0,25$. Khi đó $P(A|B)$ bằng
A. $0,2$.
B. $0,8$.
C. $0,25$.
D. $0,75$.
Câu 7. Họ tất cả các nguyên hàm của hàm số $y = 3^{2x+1}$ là:
A. $\frac{3^{2x+1}}{2\ln 3} + C$.
B. $3^{2x+1}.\ln 3 + C$.
C. $\frac{3^{2x+1}.\ln 3}{2} + C$.
D. $3^{2x+1} + C$.
Câu 8. Biết $\int_1^5 \frac{dx}{x} = \ln a$ với $a \in \mathbb{N}$. Giá trị của $a$ là
A. $125$.
B. $25$.
C. $1$.
D. $5$.
Câu 9. Ở một trường đại học, $20%$ học sinh học toán, $30%$ học lịch sử và $5%$ học cả toán và lịch sử. Chọn ngẫu nhiên một học sinh. Xác suất bạn ấy học môn lịch sử và bạn ấy học môn toán
A. $\frac{1}{3}$.
B. $\frac{1}{4}$.
C. $\frac{1}{5}$.
D. $\frac{1}{6}$.
Câu 10. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số $y = \frac{x-1}{x+2}$, trục hoành và hai đường thẳng $x = -1, x = 1$ bằng
A. $3\ln 3 – 2$.
B. $2 – 3\ln 3$.
C. $3\ln 3$.
D. $4\ln 3 – 3$.
Câu 11. Với giá trị nào của $m$ thì đường thẳng $(D): \frac{x+1}{2} = \frac{y-3}{m} = \frac{z-1}{m-2}$ vuông góc với mặt phẳng $(P): x + 3y + 2z = 2$
A. $5$.
B. $-7$.
C. $1$.
D. $6$.
Câu 12. Trong nhà sách có hai kệ sách riêng biệt A và B. Xác suất chọn được một quyển sách Toán trên kệ A và trên kệ B lần lượt là 0,3 và 0,5. Chọn ngẫu nhiên 1 quyển sách trên hai kệ sách. Giả sử quyển sách được chọn là sách Toán, xác suất quyển sách đó trên kệ B là:
A. $\frac{3}{8}$.
B. $\frac{1}{4}$.
C. $\frac{1}{3}$.
D. $\frac{5}{8}$.
B. Câu hỏi – Trả lời đúng/sai (02 điểm)
Câu 13. Một vật đang đứng yên bắt đầu chuyển động với gia tốc $a(t) = 6t + 4$ (m/s²) trong $2$ giây đầu tiên. Khi đó:
a) Kể từ khi bắt đầu chuyển động quãng đường vật di chuyển trong $2$ giây gấp $2$ lần quãng đường vật di chuyển trong $1$ giây cuối cùng.
b) Vận tốc vật có phương trình $v(t) = 3t^2 + 4t$ (m/s).
c) Kể từ khi bắt đầu chuyển động, quãng đường vật di chuyển sau $1$ giây sau $3$ mét.
d) Vận tốc vật sau $2$ giây kể từ lúc bắt đầu chuyển động là $16$ (m/s).
Câu 14. Hai chiếc khinh khí cầu bay lên từ cùng một địa điểm trong không gian. Để theo dõi hành trình của hai khinh khí cầu, người ta chọn hệ trục tọa độ $Oxyz$ với gốc $O$ đặt tại điểm xuất phát của hai khinh khí cầu, mặt phẳng $(Oxy)$ trung với mặt đất với trục $Ox$ hướng về phía Nam, trục $Oy$ hướng về phía Đông và trục $Oz$ hướng thẳng lên trời (đơn vị độ lây theo kilômét). Vào lúc $10$ giờ, chiếc thứ nhất nằm cách điểm xuất phát $3km$ về phía Đông và $2km$ về phía Nam, đồng thời cách mặt đất $0,5km$; chiếc thứ hai nằm cách điểm xuất phát $1km$ về phía Bắc và $1km$ về phía Tây, đồng thời cách mặt đất $0,3km$. Cùng thời điểm đó, một người đứng trên mặt đất và nhìn thấy hai khinh khí cầu nối trên. Biết rằng, so với các vị trí quan sát khác trên mặt đất, vị trí người đó đứng có tổng khoảng cách đến hai khinh khí cầu là nhỏ nhất. Xét tính đúng, sai trong các khẳng định sau.
a) Khoảng cách từ điểm xuất phát đến chiếc khinh khí cầu thứ nhất lúc $10h$ là $OA = \frac{\sqrt{53}}{2}$.
b) Khoảng cách giữa hai chiếc khinh khí cầu lúc $10h$ là $AB = \frac{\sqrt{626}}{5}$.
c) Tính từ lúc xuất phát đến $10h$, chiếc khinh khí cầu thứ nhất bay nhanh hơn khinh khí cầu thứ hai.
d) Tọa độ của người quan sát tại thời điểm $10h$ là $M\left(-\frac{1}{8}; \frac{1}{2}; 0\right)$.
C. Câu hỏi – Trả lời ngắn (02 điểm)
Câu 15. Cho điểm $A(-4; -2; 4)$ và đường thẳng $d: \frac{x+3}{2} = \frac{y-1}{-1} = \frac{z+1}{4}$. Gọi $\Delta$ là đường thẳng đi qua $A$, cắt và vuông góc với $d$. Biết điểm $I(a; 0; b) \in D$. Tính $a^2 + b^2$.
Đáp án số: ______
Câu 16. Một nhóm từ thiện khởi công dự án xây cầu bằng bê tông như hình vẽ (đường cong trong hình là các đường parabol). Thể tích khối bê tông dự định để đỗ cho cây cầu bằng bao nhiêu $m^3$? (kết quả làm tròn đến hàng phần mười)
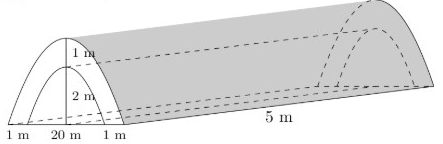
Đáp án số: ______
Câu 17. Giả sử tỉ lệ người dân của tỉnh C nghiện thuốc lá là 20%; tỉ lệ người bị bệnh phổi trong số người nghiện thuốc lá là 70%, trong số người không nghiện thuốc lá là 15%. Tính xác suất mà người đó là nghiện thuốc lá khi biết người đó bị bệnh phổi. (Kết quả làm tròn đến hàng phần trăm)
Đáp án số: ______
Câu 18. Để chuẩn bị cho một buổi triển lãm quốc tế, các trang sức có giá trị lớn được đặt bảo mật trong các khối chóp tứ giác đều $S.ABCD$ và đặt lên phía trên một trụ hình hộp chữ nhật $ABCD.A’B’C’D’$ có đáy là hình vuông (như hình vẽ). Chọn hệ trục tọa độ $Oxyz$ (đơn vị trên mỗi trục là mét) sao cho $A'(0; 0; 0)$, $A(0; 0; 1), B(0; 0; 5; 1)$. Biết rằng, ban tổ chức sự kiện dự định đặt các tấm kính cường lực hình tam giác cân có cạnh bên là 60 cm để lắp ráp thành khối chóp nối trên. Khi đó, tọa độ điểm $S$ là $(a; b; c)$. Tính giá trị của $a + b + c$. (làm tròn kết quả đến hàng phần trăm)

Đáp án số: ______
D. Câu hỏi – Trả lời tự luận (03 điểm)
Câu 19. Diện tích của hình phẳng giới hạn bởi các đường $y = \cos x, y = x + 1, x = \frac{p}{2}, x = p$ (tham khảo hình vẽ) bằng bao nhiêu?
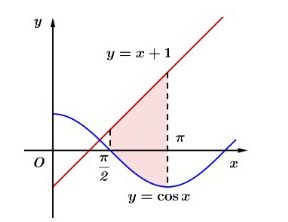
Câu 20. Trong một túi có một số chiếc kẹo cùng loại, chỉ khác màu, trong đó có 6 cái kẹo màu cam, còn lại là kẹo màu vàng. Hà lấy ngẫu nhiên một cái kẹo từ trong túi, không trả lại. Sau đó Hà lại lấy ngẫu nhiên thêm một cái kẹo khác từ trong túi. Biết rằng xác suất Hà lấy được cả hai cái kẹo màu cam là $\frac{1}{3}$. Hỏi ban đầu trong túi có bao nhiêu cái kẹo?
Câu 21. Trong không gian $Oxyz$ cho điểm $A(1; 2; 3)$ và đường thẳng $d: \frac{x-3}{2} = \frac{y-1}{1} = \frac{z+7}{-2}$. Gọi $D$ là đường thẳng đi qua $A$, vuông góc với $d$ và cắt trục $Ox$. Khoảng cách từ điểm $O$ đến đường thẳng đó bằng bao nhiêu?

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh

