Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
A. Câu hỏi – Trả lời trắc nghiệm (03 điểm)
Câu 1. Hàm số $F(x)$ là nguyên hàm của hàm số $f(x) = 3x^2$ và $F(0) = 5$. Khi đó, hàm số $F(x)$ là
A. $F(x) = x^3 + 5$.
B. $F(x) = x^3 – 5$.
C. $F(x) = 3x^3 + 5$.
D. $F(x) = 6x + 5$.
Câu 2. Trong không gian $Oxyz$, trong các mặt cầu dưới đây, mặt cầu nào có bán kính $R = 2$?
A. $(S): x^2 + y^2 + z^2 – 4x + 2y + 2z – 3 = 0$.
B. $(S): x^2 + y^2 + z^2 – 4x + 2y + 2z – 10 = 0$.
C. $(S): x^2 + y^2 + z^2 – 4x + 2y + 2z + 2 = 0$.
D. $(S): x^2 + y^2 + z^2 – 4x + 2y + 2z + 5 = 0$.
Câu 3. Biết $F(x) = x^3$ là một nguyên hàm của hàm số $f(x)$ trên I. Giá trị của $\int_0^2 [-4 + f(x)]dx$ bằng
A. $0$.
B. $-4$.
C. $12$.
D. $2$.
Câu 4. Diện tích $S$ của hình phẳng giới hạn bởi các đường $y = 2x^2$, $y = -1$, $x = 0$ và $x = 1$ được tính bởi công thức nào sau đây?
A. $S = p\int_0^1 (2x^2 + 1)dx$.
B. $S = \int_0^1 (2x^2 – 1)dx$.
C. $S = \int_0^1 (2x^2 + 1)^2 dx$.
D. $S = \int_0^1 (2x^2 + 1)dx$.
Câu 5. Trong không gian với hệ tọa độ $Oxyz$, phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm $A(1; 2; -3)$ và có vector pháp tuyến $\vec{n} = (1; -2; 3)$?
A. $x – 2y + 3z – 12 = 0$.
B. $x – 2y – 3z + 6 = 0$.
C. $x – 2y + 3z + 12 = 0$.
D. $x – 2y – 3z – 6 = 0$.
Câu 6. Trong không gian $Oxyz$, cho đường thẳng $d: \frac{x-2}{-1} = \frac{y-1}{2} = \frac{z+3}{1}$. Vector nào dưới đây là một vector chỉ phương của $d$?
A. $\vec{u_1} = (2; 1; -3)$.
B. $\vec{u_2} = (-2; -1; 3)$.
C. $\vec{u_3} = (-1; 2; 1)$.
D. $\vec{u_4} = (-1; 2; -1)$.
Câu 7. Cho hai biến cố độc lập $A, B$ với $P(A) = 0,6$, $P(B) = 0,45$. Khi đó, $P(B|A)$ bằng
A. $0,45$.
B. $0,6$.
C. $0,75$.
D. $0,15$.
Câu 8. Trong không gian $Oxyz$, cho bốn điểm $A(-2; 6; 3), B(1; 0; 6), C(0; 2; -1), D(1; 4; 0)$. Phương trình nào dưới đây là phương trình mặt phẳng $(α)$ chứa $AB$ và song song với $CD$?
A. $-x + z + 5 = 0$.
B. $x – 2y + z + 11 = 0$.
C. $x – z + 5 = 0$.
D. $x – 2y + z – 7 = 0$.
Câu 9. Một công ty bảo hiểm nhận thấy có $52%$ số người mua bảo hiểm ô tô là đàn ông và có $41,6%$ số người mua bảo hiểm ô tô là đàn ông trên 45 tuổi. Biết một người mua bảo hiểm ô tô là đàn ông, tính xác suất người đó trên 45 tuổi.
A. $0,36$.
B. $0,75$.
C. $0,8$.
D. $0,48$.
Câu 10. Cho hàm số $y = f(x)$ có đạo hàm liên tục trên $[0; 2]$, $f(0) = 1$ và $\int_0^2 f'(x)dx = -3$. Tính $f(2)$?
A. $f(2) = -4$.
B. $f(2) = 4$.
C. $f(2) = -2$.
D. $f(2) = -3$.
Câu 11. Trong không gian với hệ tọa độ $Oxyz$, viết phương trình mặt cầu tâm $I(3; 2; 4)$ và tiếp xúc với trục $Oy$.
A. $x^2 + y^2 + z^2 – 6x – 4y – 8z + 1 = 0$.
B. $x^2 + y^2 + z^2 – 6x – 4y – 8z + 2 = 0$.
C. $x^2 + y^2 + z^2 – 6z – 4y – 8z + 3 = 0$.
D. $x^2 + y^2 + z^2 – 6x – 4y – 8z + 4 = 0$.
Câu 12. Lớp 12A có 40 học sinh, trong đó có 18 học sinh thích môn Tin học, 30 học sinh thích môn Tiếng Anh, 15 học sinh không thích môn nào trong hai môn trên. Chọn ngẫu nhiên 1 học sinh. Xác suất chọn được học sinh thích môn Tin học, biết học sinh đó thích môn Tiếng Anh, là bao nhiêu?
A. $\frac{5}{8}$.
B. $\frac{3}{8}$.
C. $\frac{23}{40}$.
D. $\frac{23}{30}$.
B. Câu hỏi – Trả lời đúng/sai (02 điểm)
Câu 13. Cho hình phẳng $(S)$ giới hạn bởi đồ thị hàm số $y = f(x) = \sqrt{25 – x^2}$, trục hoành và hai đường thẳng $x = -5, x = 5$.
a) Đạo hàm của hàm số $f(x)$ bằng $\frac{x}{\sqrt{25 – x^2}}$
b) Diện tích hình phẳng $(S)$ bằng $25p$
c) Thể tích của khối tròn xoay khi quay $(S)$ quanh $Ox$ là $\frac{500}{3}p$
d) Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = f(x)$ và đường thẳng $y = 3$ bằng $K = 2\int_0^4 \sqrt{25 – x^2}dx – 12$
Câu 14. Trong không gian $Oxyz$, cho hai điểm $A(1; -3; 0), B(-5; 1; 2)$. Gọi $(P)$ là mặt phẳng trung trực của đoạn thẳng $AB$. Khi đó:
a) $\overrightarrow{AB} = (6; -4; -2)$
b) Một vector pháp tuyến của mặt phẳng $(P)$ là $\vec{n} = (12; -8; -4)$.
c) Phương trình mặt phẳng $(P)$ là: $-3x + 2y + z – 3 = 0$.
d) Gọi $(Q)$ là mặt phẳng đi qua $C(1; -3; 9)$ và song song với $(P)$ thì mặt phẳng $(Q)$ đi qua gốc tọa độ.
C. Câu hỏi – Trả lời ngắn (02 điểm)
Câu 15. Gọi $(S)$ là mặt cầu đi qua 4 điểm $A(2; 0; 0), B(1; 3; 0), C(-1; 0; 3), D(1; 2; 3)$. Bình phương bán kính $R$ của $(S)$ bằng bao nhiêu?
Đáp án số: ______
Câu 16. Nhằm tri ân người dân địa phương đã luôn tin tương, đồng hành với doanh nghiệp, tập đoàn X đã tổ chức ngày hội cầm ơn vào ngày 10/07/2024. Gọi $B(t)$ là hàm số biểu thị số lượng khách tham quan sau $t$ giờ mở cửa. Khi đó tốc độ thay đổi lượng khách tham quan trong ngày được biểu diễn bằng hàm số $B'(t) = 4t^3 – 3t^2 + 200$, trong đó $t$ tính bằng giờ $(0 \leq t \leq 8)$, $B'(t)$ tính bằng khách/giờ. Sau 2 giờ đã có 1200 người có mặt. Hỏi sau 6 giờ lượng khách tham quan là bao nhiêu người?
Đáp án số: ______
Câu 17. Một lô sản phẩm có 15 sản phẩm, trong đó có 7 sản phẩm chất lượng thấp. Lấy liên tiếp 2 sản phẩm trong 16 sản phẩm trên, trong đó sản phẩm lấy ra ở lần thứ nhất không bỏ lại vào lô sản phẩm. Tính xác suất để cả hai sản phẩm lấy được đều có chất lượng thấp.
Đáp án số: ______
**Câu 18.** Một phần mềm mô phỏng vận động viên tập bắn bia mục tiêu có kích thước nhỏ $(42 \times 42cm)$ bằng súng tiểu liên AK trong không gian $Oxyz$. Cho biết vận động viên đó sử dụng thước ngắm 3 và đứng cách xa bia mục tiêu là $100m$, trục $d$ của nòng súng và cọc đỡ bia $d’$ lần lượt có phương trình $d: \begin{cases} x = t \\ y = 2 \\ z = 4 \end{cases}$ và $d’: \begin{cases} x = 1 \\ y = 2 \\ z = 1 + 3t’ \end{cases}$. Để bắn trúng hồng tâm (điểm 10) thì vận động viên phải ngắm bắn vào điểm $N(a; b; c) \in d’$ và cách giao điểm của $d$ và $d’$ một khoảng $6cm$. Khi $c < 0$, tính giá trị biểu thức $a – b + c$.
Đáp án số: ______
D. Câu hỏi – Trả lời tự luận (03 điểm)
Câu 19. Trong một ngày bất kì, xác suất để bạn Nam ăn bữa trưa (được chuẩn bị sẵn) là $0,5$ và em gái của bạn Nam ăn bữa trưa là $0,6$. Biết rằng xác suất em gái Nam ăn bữa trưa khi Nam ăn bữa trưa là $0,9$. Tính xác suất để ít nhất một trong hai người ăn bữa trưa. (Kết quả tính biểu diễn dưới dạng phân trăm)
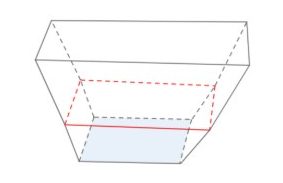
Câu 20. Một dụng cụ đựng nước có dạng như hình bên. Nếu cắt dụng cụ bằng mặt phẳng song song với mặt đáy và cách mặt đáy một khoảng $x$ (cm) $(0 \leq x \leq 5)$ thì được thiết diện là hình chữ nhật có chiều dài là $2x$ (cm) và chiều rộng là $\sqrt{x + 3}$ (cm). Dung tích của dụng cụ trên là bao nhiêu? (Kết quả làm tròn đến chữ số thập phân hàng phần chục).
Câu 21. Giả sử Trái Đất có dạng hình cầu bán kính bằng $6,4.10^6 m$. Bạn An đang đứng trên mặt đất. Có 3 vệ tinh bảo vệ máy chủ tiếp nhận thông tin rằng vệ tinh thứ nhất đang cách An $3.10^6 m$, vệ tinh thứ hai đang cách An $4.10^6 m$ và vệ tinh thứ ba đang cách An $5.10^6 m$. Biết rằng trong hệ trục tọa độ $Oxyz$ cho trước với $O$ là tâm Trái Đất (1 đơn vị = $10^6 m$), tại thời điểm vệ tinh thông báo về máy chủ thì tọa độ của các vệ tinh lần lượt là $I_1(4; 4; 6)$, $I_2(8; 4; 3)$ và $I_3(4; 9; 3)$. Hãy tìm tọa độ vị trí của bạn An.


ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh

