Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
A. Câu hỏi – Trả lời trắc nghiệm (03 điểm)
Câu 1. Họ tất cả các nguyên hàm của hàm số $f(x) = x^3$ là
A. $4x^4 + C$.
B. $3x^2 + C$.
C. $x^4 + C$.
D. $\frac{1}{4}x^4 + C$.
Câu 2. Cho hai biến cố độc lập $A$ và $B$ với $0 < P(A) < 1$, $0 < P(B) < 1$. Chọn khẳng định đúng trong các khẳng định sau
A. $P(A) = P(B|A)$.
B. $P(A) = P(B|A).P(A \cap B)$.
C. $P(A) = P(A|B)$.
D. $P(A) = P(A|B).P(B)$.
Câu 3. Cho hàm số $y = f(x)$ liên tục trên $[a; b]$. Mệnh đề nào sau đây đúng?
A. $\int_a^b f(x)dx = \int_a^c f(x)dx$.
B. $\int_a^b f(x)dx = -\int_b^a f(x)dx$.
C. $\int_a^b f(x)dx = 2\int_a^b f(x)d(2x)$.
D. $\int_a^b 2025f(x)dx = 2025$.
Câu 4. Giá trị của $\int_0^p \sin x dx$ bằng
A. $\frac{1}{2}$.
B. $-\frac{3}{2}$.
C. $-\frac{1}{2}$.
D. $\frac{3}{2}$.
Câu 5. Trong không gian $Oxyz$, mặt phẳng $(P): x + y + z – 3 = 0$ đi qua điểm nào dưới đây?
A. $M(-1; -1; -1)$.
B. $N(1; 1; 1)$.
C. $P(-3; 0; 0)$.
D. $Q(0; 0; -3)$.
Câu 6. Cho hàm số $y = f(x)$ liên tục trên I có đồ thị như hình vẽ. Gọi $(H)$ là hình phẳng được giới hạn bởi các đường thẳng $x = -1, x = 2$, đồ thị $y = f(x)$ và trục hoành. Khi đó khẳng định nào dưới đây là đúng?
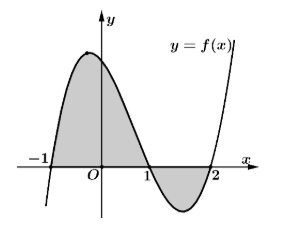
A. $S_{(H)} = \int_{-1}^2 f(x)dx$.
B. $S_{(H)} = \int_{-1}^1 f(x)dx + \int_1^2 f(x)dx$.
C. $S_{(H)} = \int_{-1}^1 f(x)dx – \int_1^2 f(x)dx$.
D. $S_{(H)} = -\int_{-1}^1 f(x)dx + \int_1^2 f(x)dx$.
Câu 7. Lớp 12A1 có 48 bạn đều giỏi ít nhất một trong hai môn Toán và Lý, trong đó có 36 bạn giỏi Toán, 24 bạn giỏi Lý. Chọn ngẫu nhiên 1 bạn. Xác suất chọn được bạn giỏi Toán, biết bạn đó giỏi Lý là bao nhiêu?
A. $\frac{5}{8}$.
B. $\frac{3}{8}$.
C. $\frac{1}{2}$.
D. $\frac{1}{3}$.
Câu 8. Một ô tô đang chạy với vận tốc $15$ (m/s) thì tăng tốc chuyển động nhanh dần với gia tốc $a = t + 2$ (m/s²), trong đó $t$ là khoảng thời gian tính bằng giây kể từ lúc tăng vận tốc và $0 < t \leq 10$. Hỏi tại giây thứ $9$ thì vận tốc của ô tô là bao nhiêu (m/s)?
A. $85,3$ (m/s).
B. $83,5$ (m/s).
C. $73,5$ (m/s).
D. $75,3$ (m/s).
**Câu 9.** Trong không gian $Oxyz$, cho hai đường thẳng $d_1: \frac{x-1}{2} = \frac{y+2}{3} = \frac{z-3}{4}$ và $d_2: \begin{cases} x = 3 + 4t \\ y = 5 + 6t \\ z = 7 + 8t \end{cases}$ $(t \in \mathbb{R})$. Trong các mệnh đề sau, mệnh đề nào đúng?
A. $d_1$ và $d_2$ chéo nhau.
B. $d_1 \equiv d_2$.
C. $d_1 \perp d_2$.
D. $d_1 // d_2$.
Câu 10. Khi cắt một vật thể bởi mặt phẳng vuông góc với trục $Ox$ tại điểm có hoành độ $x$, $\left(-\sqrt{3} \leq x \leq \sqrt{3}\right)$, mặt cắt là hình vuông có độ dài các cạnh là $\sqrt{3 – x^2}$. Thể tích của vật thể đã cho bằng
A. $\sqrt{3}$.
B. $4\sqrt{3}$.
C. $4p\sqrt{3}$.
D. $p\sqrt{3}$.
Câu 11. Trong không gian $Oxyz$, cho $A(1; 2; 3)$, $B(3; 4; 4)$. Tìm tất cả các giá trị của tham số $m$ sao cho khoảng cách từ điểm $A$ đến mặt phẳng $2x + y + mz – 1 = 0$ bằng độ dài đoạn thẳng $AB$.
A. $m = 2$.
B. $m = -2$.
C. $m = -3$.
D. $m = \pm 2$.
Câu 12. Trong không gian $Oxyz$, hãy tính số đo góc $a$ giữa đường thẳng $D: \frac{x}{1} = \frac{y}{2} = \frac{z-1}{-1}$ và mặt phẳng $(P): x – y + 2z + 1 = 0$.
A. $a = 30°$.
B. $a = 60°$.
C. $a = 150°$.
D. $a = 120°$.
B. Câu hỏi – Trả lời đúng/sai (02 điểm)
Câu 13. Trong không gian tọa độ $Oxyz$, cho mặt cầu $(S): (x + 1)^2 + (y – 2)^2 + (z + 3)^2 = 4$. Khi đó:
a) Tọa độ tâm $I$ của mặt cầu $(S)$ là $I(-1; 2; -3)$.
b) Mặt cầu $(S)$ đi qua điểm $A(1; 2; 3)$.
c) Điểm $B(2; -1; 3)$ nằm bên ngoài mặt cầu $(S)$.
d) Đường thẳng $d: \begin{cases} x = -t \\ y = 1 + 2t \\ z = 3 + t \end{cases}$ cắt mặt cầu $(S)$ tại hai điểm phân biệt.
Câu 14. Rùa và thỏ tranh tài: Trong một cuộc thi chạy đua giữa rùa và thỏ xem ai chạy được quãng đường xa hơn, rùa chạy với tốc độ $v_R(t) = 3\sqrt{t}$, thỏ chạy với tốc độ $v_T(t) = 5 – 5\cos(2pt)$ (với $t$ là thời gian (đơn vị: giờ), vận tốc đơn vị $km/h$). (Các kết quả làm tròn đến hàng phần trăm, đơn vị $km$)
a) Trong khoảng thời gian từ $0,5$ giờ đến $1$ giờ (kể từ khi xuất phát) thì vận tốc của thỏ giảm dần.
b) Quãng đường rùa chạy được sau $0,5$ giờ là $0,70km$.
c) Nếu cuộc đua kết thúc sau $1$ giờ thì thỏ giành chiến thắng và thắng cách biệt $3,15km$.
d) Nếu cuộc đua kết thúc khi thỏ hoặc rùa chạy được $10km$ đầu tiên thì thỏ giành chiến thắng và thắng cách biệt $4,34km$.
C. Câu hỏi – Trả lời ngắn (02 điểm)
Câu 15. Biết $F(x) = (ax^2 + bx + c)\sqrt{2x – 4}$ là một nguyên hàm của hàm số $f(x) = \frac{10x^2 – 13x – 252}{\sqrt{2x – 4}}$ trên khoảng $(2; +\infty)$. Tính giá trị biểu thức $T = abc$.
Đáp án số: ______
Câu 16. Trong không gian $Oxyz$, cho mặt phẳng $(P): x + 2y = 0$. Đường thẳng đi qua $A(-1; 3; -4)$ cắt trục $Ox$ và song song với mặt phẳng $(P)$ có một vector chỉ phương là: $\vec{u} = (a; b; 4)$. Tính giá trị $a^2 + b$.
Đáp án số: ______
Câu 17. Cho đồ thị hàm số $y = f(x) = x^2$ và đường thẳng $y = g(x) = mx + n$ như hình vẽ dưới đây:
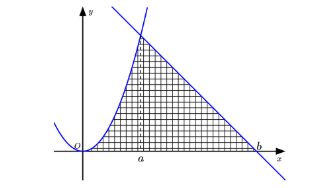
Nếu $a = 3, b = 9$. Khi đó diện tích phần gạch như hình trên bằng
Đáp án số: ______
Câu 18. Trường THPT X muốn làm một cái cửa nhà hình parabol có chiều cao từ mặt đất đến đỉnh là $2,25$ mét, chiều rộng tiếp giáp với mặt đất là $3$ mét. Giá thuê mỗi mét vuông là $1500000$ đồng. Vậy số tiền nhà trường phải trả là bao nhiêu (Đơn vị triệu đồng)?(Làm tròn đến hàng phần trăm).
Đáp án số: ______
D. Câu hỏi – Trả lời tự luận (03 điểm)
Câu 19. Tỉ lệ người nghiện thuốc lá ở một vùng là $30%$. Biết tỉ lệ viêm họng trong số người nghiện thuốc lá là $a%$ còn người không nghiện là $40%$. Gặp ngẫu nhiên một người trong vùng thì xác suất để người đó nghiện thuốc và bị viêm họng bằng $0,21$; xác suất để người đó không nghiện thuốc và bị viêm họng là $b%$. Tính $a + b$.
Câu 20. Trong không gian $Oxyz$, cho $A(2; 0; 0), B(0; 4; 0), C(0; 0; 6)$. Gọi $(P)$ là mặt phẳng không chứa gốc tọa độ và song song với $mp(ABC)$, biết khoảng cách giữa mặt phẳng $(P)$ và mặt phẳng $(ABC)$ bằng $\frac{12}{7}$. Viết phương trình của mặt phẳng $(P)$.
Câu 21. Trong không gian $Oxyz$, cho đường thẳng $D$ là giao tuyến của hai mặt phẳng $(P): z – 1 = 0$ và $(Q): x + y + z – 3 = 0$. Gọi $d$ là đường thẳng nằm trong mặt phẳng $(P)$, cắt đường thẳng $\frac{x-1}{1} = \frac{y-2}{-1} = \frac{z-3}{-1}$ và vuông góc với đường thẳng $D$. Viết phương trình của đường thẳng $d$.

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh

