Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Hàm số nào sau đây là một nguyên hàm của hàm số $y = 4\sin x – \cos x$?
A. $-4\cos x – \sin x$.
B. $4\cos x + \sin x + 1$.
C. $4\cos x + \sin x$.
D. $4\cos x – \sin x – 3$.
Câu 2. Cho $F(x)$ là một nguyên hàm của hàm số $f(x) = 3x^2$ và $F(0) = 4$. Tìm $F(x)$
A. $F(x) = x^3$.
B. $F(x) = 3x^3 + 4$.
C. $F(x) = x^3 – 1$.
D. $F(x) = x^3 + 4$.
Câu 3. Cho F(x) là một nguyên hàm của hàm số f(x), $\int_a^b f(x)dx = 10$ và $F(a) = -4$. Tính $F(b)$
A. $F(b) = 9$.
B. $F(b) = 14$.
C. $F(b) = 12$.
D. $F(b) = 6$.
Câu 4. Biết $\int_1^4 f(x)dx = 7$ và $\int_1^4 g(x)dx = 4$. Tính $I = \int_1^4 [2f(x) – 3g(x)]dx$?
A. $I = 2$.
B. $I = 9$.
C. $I = 26$.
D. $I = 4$.
Câu 5. Biết $\int_0^3 f(x)dx = -1$ và $\int_0^1 f(x)dx = 9$. Tính $I = \int_1^3 f(x)dx$?
A. $I = -8$.
B. $I = 8$.
C. $I = -10$.
D. $I = 10$.
Câu 6. Tính diện tích S của hình phẳng giới hạn bởi các đường: $y = 2x^2 – 4, y = x^2 + 3x$
A. $S = \frac{625}{6}\pi$.
B. $S = \frac{125}{6}$.
C. $S = \frac{125}{6}\pi$.
D. $S = \frac{625}{6}$.
Câu 7. Thể tích $V$ của khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi đồ thị hàm số $y = x^2$ và các đường thẳng $y = 0$, $x = 1$, $x = 2$ xung quanh trục hoành là
A. $V = \frac{7}{3}$.
B. $V = \frac{31\pi}{5}$.
C. $V = \frac{7\pi}{3}$.
D. $V = \frac{31}{5}$.
Câu 8. Trong không gian $Oxyz$, cho mặt phẳng $(P): 4x – 3y – z + 1 = 0$. Tọa độ vectơ pháp tuyến của (P) là
A. $(4; -3; -1)$.
B. $(4; 3; -1)$.
C. $(2; -3; -1)$.
D. $(4; -3; 1)$.
Câu 9. Trong không gian $Oxyz$, viết phương trình đường thẳng $\Delta$ đi qua $M(4; 0; -2)$ và có vectơ chỉ phương $\vec{u} = (1; 3; -2)$
A. $\Delta: \frac{x-1}{4} = \frac{y-3}{1} = \frac{z+2}{-2}$.
B. $\Delta: \frac{x+4}{1} = \frac{y}{3} = \frac{z-2}{-2}$.
C. $\Delta: \frac{x-4}{1} = \frac{y}{3} = \frac{z+2}{-2}$.
D. $\Delta: \frac{x+1}{4} = \frac{y+3}{1} = \frac{z-2}{-2}$.
Câu 10. Trong không gian Oxyz, cho mặt cầu $(S): (x-5)^2 + (y+4)^2 + z^2 = 9$. Hãy tìm tọa độ tâm $I$ và bán kính $R$ của mặt cầu $(S)$?
A. $I(5; 4; 0), R = 3$.
B. $I(-5; 4; 0), R = 9$.
C. $I(5; -4; 0), R = 9$.
D. $I(5; -4; 0), R = 3$.
Câu 11. Cho hai biến cố $A$ và $B$ có $P(B) = 0,7$, $P(A \cap B) = 0,3$. Tính $P(A|B)$.
A. $\frac{3}{7}$.
B. $\frac{1}{2}$.
C. $\frac{6}{7}$.
D. $\frac{1}{7}$.
Câu 12. Cho hai biến cố $A$ và $B$ có $P(B) = 0,8$, $P(A|B) = 0,7$, $P(A|\overline{B}) = 0,45$. Tính $P(A)$.
A. $0,25$.
B. $0,65$.
C. $0,55$.
D. $0,5$.
PHẦN II. Câu trắc nghiệm đúng sai
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số $y = f(x)$ có đồ thị như hình vẽ và gọi S là diện tích phần tô màu
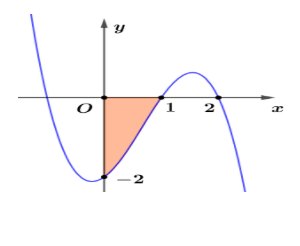
a) $S = \int_{-2}^1 |f(x)|dx$.
b) $S = \int_1^2 f(x)dx$.
c) $S = \int_0^1 |f(x)|dx$.
d) $S = \int_0^1 f(x)dx$.
**Câu 2.** Trong không gian $Oxyz$, cho hai đường thẳng $d_1: \begin{cases} x = 1 + 2t \\ y = -2 + t \\ z = 2t \end{cases}$ và $d_2: \frac{x-3}{1} = \frac{y-4}{-2} = \frac{z-5}{2}$. Gọi $\alpha$ là góc giữa hai đường thẳng $d_1, d_2$.
a) Vectơ $\vec{n_1}(1; -2; 0)$ là một vectơ chỉ phương của đường thẳng $d_1$.
b) Vectơ có tọa độ $(1; -2; 2)$ là một vectơ chỉ phương của đường thẳng $d_2$.
c) $\cos \alpha = \frac{|\vec{u_1}.\vec{u_2}|}{|\vec{u_1}|.|\vec{u_2}|}$ với $\vec{u_1}, \vec{u_2}$ lần lượt là vectơ chỉ phương của đường thẳng $d_1, d_2$.
d) $\alpha \approx 64°$ (làm tròn đến hàng đơn vị của độ).
Câu 3. Trong không gian $Oxyz$, cho hai điểm $A(-2; 1; 1)$ và $B(0; -1; 1)$.
a) Mặt cầu đường kính AB có tâm là trung điểm của đoạn thẳng AB.
b) Nếu I là trung điểm của AB thì $I(-1; 0; 2)$.
c) Bán kính mặt cầu đường kính AB bằng 2.
d) Phương trình mặt cầu đường kính AB là $(x+1)^2 + y^2 + (z-1)^2 = 2$.
Câu 4. Cho hai biến cố $A$ và $B$, với $P(A) = 0,4$, $P(B) = 0,8$, $P(A \cap B) = 0,4$.
a) $P(A) = 0,6$ và $P(\overline{B}) = 0,2$.
b) $P(A|B) = \frac{1}{2}$.
c) $P(\overline{B}|A) = \frac{2}{3}$.
d) $P(\overline{A} \cap B) = \frac{3}{5}$.
PHẦN III. Câu trắc nghiệm trả lời ngắn
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Một vật chuyển động với vận tốc thay đổi theo thời gian được tính bởi công thức $v(t) = 5t + 1$, thời gian tính theo đơn vị giây, quãng đường vật đi được tính theo đơn vị mét. Tính quãng đường vật đó đi được trong 10 giây đầu tiên.
Câu 2. Trong không gian Oxyz (đơn vị trên các trục là kilomet), cho một trạm thu phát sóng 5G có bán kính vùng phủ sóng của trạm là 5 km đặt ở vị trí $I(6; -2; 4)$. Tìm giá trị lớn nhất của m (làm tròn đến hàng đơn vị) để một người dùng điện thoại ở vị trí $A(m + 4; m; 4)$ có thể sử dụng dịch vụ của trạm nói trên.
Câu 3. Một phần mềm mô phỏng vận động viên đang tập bắn súng trong không gian Oxyz. Cho biết trục d của nòng súng có phương trình $\frac{x-1}{1} = \frac{y-2}{-3} = \frac{z-3}{-5}$ và hồng tâm $A(8; -19; 6m + 4)$. Hỏi m bằng bao nhiêu để vận động viên bắn trúng hồng tâm?

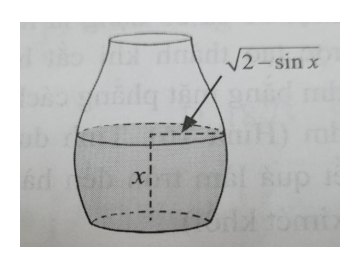
Câu 4. Một bình chứa nước có dạng như hình bên có chiều cao là $\frac{3\pi}{2}$ (dm). Nếu lượng nước trong bình có chiều cao $x$ (dm) thì mặt nước là hình tròn có bán kính là $\sqrt{2-\sin x}$ (dm) với $0 \leq x \leq \frac{3\pi}{2}$. Tính dung tích của bình (làm tròn kết quả đến hàng phần trăm của đêximét khối).
Câu 5. Trong một đợt thi chứng chỉ hành nghề có 150 người tham gia, trong đó có 80 nam và 70 nữ. Khi công bố kết quả kì thi đó, có 41 người đạt loại giỏi, trong đó có 22 nam và 19 nữ. Chọn ngẫu nhiên một người, tính xác suất để người được chọn ra đạt loại giỏi và là nữ (làm tròn kết quả đến hàng phần trăm).
Câu 6. Hộp thứ nhất có 5 tấm thẻ được đánh số từ 1 đến 5. Hộp thứ hai có 4 tấm thẻ được đánh số từ 1 đến 4. Lấy ngẫu nhiên một thẻ từ hộp thứ nhất và bỏ vào hộp thứ hai. Sau đó lấy ngẫu nhiên ra 2 thẻ từ hộp thứ hai. Tính xác suất để tích các số ghi trên 2 thẻ lấy ra là số chẵn.

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh