PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1. Họ nguyên hàm của hàm số $f(x) = x^3$ là

A. $F(x) = 3x^2 + C$.

B. $F(x) = \frac{x^4}{4} + C$.

C. $F(x) = x^2$.

D. $F(x) = \frac{x^4}{3} + C$.

Câu 2. Cho $\int_0^1 f(x)dx = 3$ và $\int_1^3 f(x)dx = -2$. Tính $\int_0^3 f(x)dx$.

A. $5$.

B. $1$.

C. $-5$.

D. $-1$.

Câu 3. Nếu $\int_0^2 f(x)dx = 2$ thì $\int_0^2 [4x – f(x)]dx$ bằng

A. $12$.

B. $10$.

C. $4$.

D. $6$.

Câu 4. Cho hàm số $y = f(x)$ liên tục trên $\mathbb{R}$. Gọi $S$ là diện tích hình phẳng giới hạn bởi các đường $y = f(x)$, $y = 0$, $x = -1$ và $x = 4$ (như hình vẽ bên).

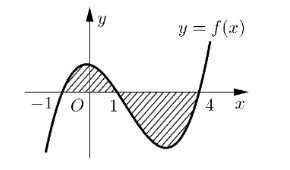
Mệnh đề nào dưới đây là đúng?

A. $S = \int_{-1}^1 f(x)dx + \int_1^4 f(x)dx$.

B. $S = \int_{-1}^1 f(x)dx – \int_1^4 f(x)dx$.

C. $S = -\int_{-1}^1 f(x)dx + \int_1^4 f(x)dx$.

D. $S = -\int_{-1}^1 f(x)dx – \int_1^4 f(x)dx$.

Câu 5. Cho hai biến cố $A, B$ sao cho $P(A) = 0,5$, $P(B) = 0,7$, $P(A|B) = 0,3$. Tính $P(B|A)$.

A. $\frac{5}{7}$.

B. $\frac{3}{7}$.

C. $\frac{6}{7}$.

D. $\frac{21}{50}$.

Câu 6. Tìm một vectơ pháp tuyến của mặt phẳng $(P): 2x – y + 3z – 2 = 0$.

A. $\vec{n} = (2; 1; 3)$.

B. $\vec{n} = (2; -1; 3)$.

C. $\vec{n} = (-2; -1; 3)$.

D. $\vec{n} = (2; -1; -3)$.

Câu 7. Trong không gian $Oxyz$, cho hai điểm $A(2; 4; 1), B(-1; 1; 3)$ và mặt phẳng $(P): x – 3y + 2z – 5 = 0$. Lập phương trình mặt phẳng $(Q)$ đi qua hai điểm $A$, $B$ và vuông góc với mặt phẳng $(P)$.

A. $2y + 3z – 11 = 0$.

B. $2x – 3y – 11 = 0$.

C. $x – 3y + 2z – 5 = 0$.

D. $3y + 2z – 11 = 0$.

**Câu 8.** Trong không gian $Oxyz$, cho đường thẳng $d: \begin{cases} x = 2 + t \\ y = 1 – 2t \\ z = -1 + 3t \end{cases}$. Vectơ nào dưới đây là một vectơ chỉ phương của $d$?

A. $\vec{u_1} = (2; 1; -1)$.

B. $\vec{u_2} = (1; 2; 3)$.

C. $\vec{u_3} = (1; -2; 3)$.

D. $\vec{u_4} = (2; 1; 1)$.

Câu 10. Trong không gian $Oxyz$, mặt cầu $(S): (x+1)^2 + (y-2)^2 + z^2 = 9$ có bán kính bằng

A. $3$.

B. $81$.

C. $9$.

D. $6$.

Câu 11. Trong không gian $Oxyz$, mặt cầu $(S)$ có tâm $I(3; -3; 1)$ và đi qua điểm $A(5; -2; 1)$ có phương trình là

A. $(x-3)^2 + (y+3)^2 + (z-1)^2 = 5$.

B. $(x-3)^2 + (y+3)^2 + (z-1)^2 = 5$.

C. $(x-5)^2 + (y+2)^2 + (z-1)^2 = 25$.

D. $(x-3)^2 + (y+3)^2 + (z-1)^2 = \sqrt{5}$.

Câu 12. Một chất điểm $A$ xuất phát từ $O$, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật $v(t) = \frac{1}{150}t^2 + \frac{59}{75}$ (m/s), trong đó $t$ (giây) là khoảng thời gian tính từ lúc $a$ bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm $B$ cũng xuất phát từ $O$, chuyển động thẳng cùng hướng với $A$ nhưng chậm hơn 3 giây so với $A$ và có gia tốc bằng $a$ (m/s²) ($a$ là hằng số). Sau khi $B$ xuất phát được 12 giây thì đuổi kịp $A$. Vận tốc của $B$ tại thời điểm đuổi kịp $A$ bằng

A. $15$ (m/s).

B. $20$ (m/s).

C. $16$ (m/s).

D. $13$ (m/s).

PHẦN II. Câu trắc nghiệm đúng sai

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1. Cho hàm số $f(x) = x^2 – 2x$ có đồ thị là parabol $(P)$. Gọi $(H)$ là hình phẳng giới hạn bởi $(P)$ và trục hoành.

a) $\int_0^2 f(x) = -\frac{2}{3}$.

b) Một nguyên hàm của $f(x)$ là $F(x) = 2x – 2$.

c) Diện tích hình phẳng $(H)$ bằng $\frac{4}{3}$.

d) Thể tích khối tròn xoay khi cho hình phẳng $(H)$ quay quanh trục $Ox$ bằng $\frac{16}{15}$.

Câu 2. Trong không gian tọa độ $Oxyz$, cho đường thẳng $d$ đi qua hai điểm $A(1; 2; 1), B(3; 0; 1)$, mặt phẳng $(a)$ đi qua ba điểm $M(0; 1; 0), N(2; 1; 3), P(4; 1; 1)$.

a) Vectơ $(1; -1; 0)$ là một vectơ chỉ phương của đường thẳng $d$.

b) Mặt phẳng $(a)$ có một vectơ pháp tuyến có tọa độ là $M(0; 1; 0)$.

c) Mặt cầu đường kính $AB$ có phương trình là $(x-2)^2 + (y-1)^2 + (z-1)^2 = 8$.

d) Góc giữa đường thẳng $d$ và mặt phẳng $(a)$ bằng $45°$.

Câu 3. Một ô tô đang chạy với vận tốc $65$ km/h thì người lái xe bất ngờ phát hiện chướng ngại vật trên đường cách đó $50$ m. Người lái xe phản ứng một giây, sau đó đạp phanh khẩn cấp. Kể từ thời điểm này, ô tô chuyển động chậm dần đều với tốc độ $v(t) = -10t + 20$ (m/s), trong đó $t$ là thời gian tính bằng giây kể từ lúc đạp phanh. Gọi $s(t)$ là quãng đường ô tô đi được trong thời gian $t$ (giây) kể từ lúc đạp phanh.

a) $s(t)$ là một nguyên hàm của $v(t)$.

b) $s(t) = -5t^2 + 20t$.

c) Thời gian kể từ lúc đạp phanh đến lúc ô tô dừng hẳn là $20$ giây.

d) Xe ô tô không va vào chướng ngại vật trên đường.

Câu 4. Lớp 12A có 40 học sinh, trong đó có 25 học sinh tham gia câu lạc bộ Tiếng Anh, 16 học sinh tham gia câu lạc bộ Toán Học, 12 học sinh tham gia cả hai câu lạc bộ Tiếng Anh và Toán Học. Chọn ngẫu nhiên một học sinh. Xét các biến cố sau:

A: “Học sinh được chọn tham gia câu lạc bộ Tiếng Anh”.

B: “Học sinh được chọn tham gia câu lạc bộ Toán Học”.

a) $P(A) = 0,4$.

b) $P(B) = 0,625$.

c) $P(A|B) = 0,75$.

d) $P(B|A) = 0,48$.

PHẦN III. Câu trắc nghiệm trả lời ngắn

Thí sinh trả lời từ câu 1 đến câu 5.

Câu 1. Cho $F(x)$ là một nguyên hàm của hàm số $f(x) = \frac{1}{x-2}$, biết $F(1) = 2$. Tính giá trị của $F(0)$ (làm tròn kết quả đến hàng phần trăm).

Câu 2. Cho $\int_a^b |x|dx = ma^2 + nb^2$ với $m, n, a, b$ là các hằng số thực và $a < 0 < b$. Tính giá trị của $m + n$.

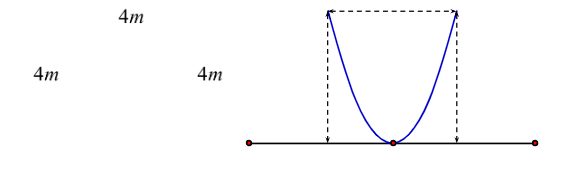
Câu 3. Một khuôn viên dạng nửa hình tròn, trên đó người thiết kế phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm và có trục đối xứng vuông góc với đường kính của nửa hình tròn, hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô màu) và cách nhau một khoảng bằng $4(m)$. Phần còn lại của khuôn viên (phần không tô màu) dành để trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ, chi phí để trồng hoa và cỏ Nhật Bản tương ứng là $150.000$ đồng/m² và $100.000$ đồng/m². Hỏi cần bao nhiêu tiền để trồng hoa và trồng cỏ Nhật Bản trong khuôn viên đó? (Số tiền được làm tròn đến hàng đơn vị)

Câu 4. Có 40 chiếc thẻ được đánh số từ 1 đến 40. Một người rút ngẫu nhiên lần lượt hai tấm thẻ (rút không hoàn lại). Tính xác suất để lần thứ hai rút được thẻ mang số nguyên tố.

Câu 5. Trong không gian $Oxyz$, cho điểm $A(0; 1; 2)$ và đường thẳng $d: \frac{x-2}{2} = \frac{y-1}{2} = \frac{z-1}{-3}$. Gọi $(P)$ là mặt phẳng đi qua $A$ và chứa $d$. Khoảng cách từ điểm $M(5; -1; 3)$ đến $(P)$ bằng

A. $5$.

B. $\frac{1}{3}$.

C. $1$.

D. $\frac{11}{3}$.

Câu 6. Trong không gian $Oxyz$, đài kiểm soát không lưu sân bay có tọa độ $O(0; 0; 0)$, đơn vị trên mỗi trục tính theo $km$. Một máy bay chuyển động hướng về đài kiểm soát không lưu, bay qua hai vị trí $A(-500; -250; 150), B(-200; -200; 100)$. Khi máy bay gần đài kiểm soát nhất, tọa độ vị trí máy bay là $(a; b; c)$. Giá trị của biểu thức $-3a – b – c$ bằng bao nhiêu (làm tròn kết quả đến hàng đơn vị)?

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh