Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1:
Cho hàm số bậc năm $y = f(x)$ có đồ thị như hình vẽ.
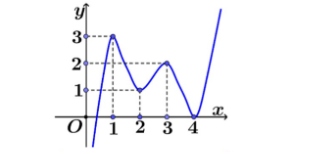
Hàm số nghịch biến trong khoảng nào dưới đây?
A. $(1; 3)$
B. $(2; 4)$
C. $(-\infty; 1)$
D. $(1; 2)$
Câu 2:
Cho hàm số bậc ba $y = f(x)$ có có đồ thị là đường cong như hình bên dưới
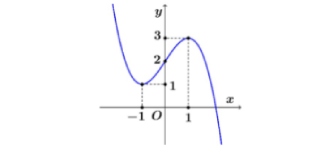
Giá trị cực tiểu của hàm số đã cho là
A. $-3$
B. $3$
C. $1$
D. $-1$
Câu 3:
Số đường tiệm cận của đồ thị hàm số $y = -x + 3 – \frac{5}{2x-1}$ là
A. $4$
B. $2$
C. $1$
D. $3$
Câu 4:
Biết giá trị lớn nhất của hàm số $y = \frac{\ln^2 x}{x}$ trên đoạn $[1; e^3]$ là $M = \frac{a}{e^b}$, trong đó $a, b$ là các số tự nhiên. Khi đó $3a^2 + b^3$ bằng
A. $32$
B. $24$
C. $56$
D. $135$
Câu 5:
Cho hình lăng trụ tam giác $ABC.A’B’C’$. Gọi $M, N$ lần lượt là trung điểm của $AB, AC$. Khi đó $\overrightarrow{MN}$ bằng
A. $\frac{1}{2}\overrightarrow{AB}$
B. $\overrightarrow{NC}$
C. $\overrightarrow{AM}$
D. $\frac{1}{2}\overrightarrow{B’C’}$
Câu 6:
Trong các điểm sau đây, điểm nào thuộc đồ thị của hàm số $y = x^3 + x + 2$
A. $(1; 0)$
B. $(1; 3)$
C. $(1; 1)$
D. $(1; 4)$
Câu 7:
Trong không gian, cho hai véc tơ $\vec{a}$ và $\vec{b}$ có cùng độ dài bằng 2. Biết góc giữa hai véc tơ đó là $30°$. Tính $\vec{a} \cdot \vec{b}$.
A. $1$
B. $\sqrt{3}$
C. $2$
D. $2\sqrt{3}$
Câu 8:
Cho hình lập phương $ABFE.DCHG$.
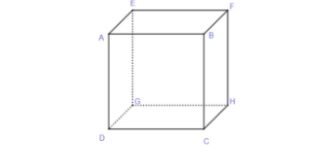
Véc tơ $\overrightarrow{GC}$ bằng véc tơ nào sau đây?
A. $\overrightarrow{EB}$
B. $\overrightarrow{GH}$
C. $\overrightarrow{CG}$
D. $\overrightarrow{DC}$
Câu 9:
Cho hàm số $y = \frac{ax + b}{cx + d}$, $(c \neq 0, ad – cb \neq 0)$ có đồ thị là đường cong trong hình bên. Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là
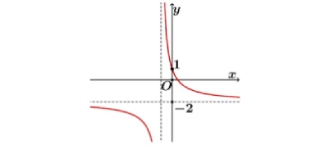
A. $(1; 0)$
B. $(0; 1)$
C. $(-2; 0)$
D. $(0; -1)$
Câu 10:
Cho hàm số bậc bốn $y = f(x)$. Hàm số $y = f'(x)$ có đồ thị như hình vẽ.
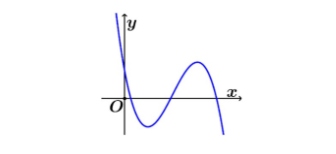
Số điểm cực trị của hàm số $y = f(x)$ là
A. $0$
B. $1$
C. $2$
D. $3$
Câu 11:
Đồ thị của hàm số nào sau đây có dạng như hình vẽ bên.
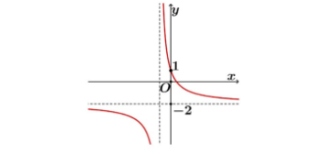
A. $y = \frac{1-2x}{x+1}$
B. $y = \frac{1-2x}{x-1}$
C. $y = \frac{3-2x}{x+1}$
D. $y = \frac{1-2x}{1-x}$
Câu 12:
Tiệm cận xiên của đồ thị hàm số $y = \frac{x^2-x-1}{x-2}$ là đường thẳng có phương trình:
A. $y = -x$
B. $y = -x-1$
C. $y = -x+1$
D. $y = x+1$
PHẦN II. Câu trắc nghiệm đúng sai
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1:
Cho đồ thị hàm số $y = f(x)$ có hình vẽ dưới đây và có tập xác định trên $\mathbb{R}$.
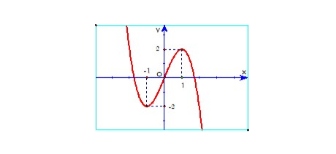
a) Đồ thị hàm số đã cho là đồ thị của hàm số bậc ba.
b) Hàm số đã cho nghịch biến trên khoảng $(-1; 1)$.
c) Đồ thị hàm số đã cho là hàm số $y = x^3 – 3x$.
d) Hàm số đã cho có hai điểm cực trị.
Câu 2:
Trong không gian $Oxyz$, cho hình lập phương $ABCD.A’B’C’D’$ có cạnh bằng $a$.
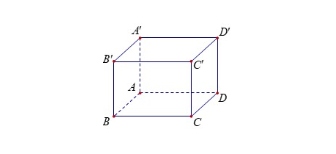
a) $\overrightarrow{A’C’} \cdot \overrightarrow{BC} = a^2$.
b) Góc giữa hai vectơ $\overrightarrow{AC}$ và $\overrightarrow{B’D’}$ bằng $45°$.
c) $\overrightarrow{AC} = \overrightarrow{A’C’}$.
d) $\overrightarrow{CA’} = \overrightarrow{CC’} + \overrightarrow{CB} + \overrightarrow{CD}$.
Câu 3:
Cho hàm số $y = \frac{x+6}{x+m}$ (với $m$ là tham số, $m \neq 6$).
a) Hàm số không có cực trị.
b) Hàm số đồng biến trên khoảng $(-\infty; -10)$ khi và chỉ khi $m \in (6; 10]$.
c) Tập xác định của hàm số là $\mathbb{R}$.
d) Hàm số đồng biến trên từng khoảng xác định khi và chỉ khi $m > 6$.
Câu 4:
Cho đồ thị của hàm số $y = f(x) = \frac{x^2 + 3x}{x + 2}$.
a) Hàm số $y = f(x)$ đồng biến trên khoảng $(0; 1)$
b) Đồ thị hàm số $y = f(x)$ nhận đường thẳng $y = x – 1$ làm tiệm cận xiên
c) Hàm số có đạo hàm $y’ = \frac{x^2 + 4x + 6}{(x + 2)^2}$
d) Giá trị lớn nhất của hàm số $y = f(x)$ trên đoạn $[-1; 0]$ là $0$
PHẦN III. Câu trắc nghiệm trả lời ngắn
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1:
Một đường dây điện được nối từ một nhà máy điện ở $A$ đến một hòn đảo ở $C$ như Hình. Khoảng cách từ $C$ đến $B$ là $6km$. Bờ biển chạy thẳng từ $A$ đến $B$ với khoảng cách là $10km$. Tổng chi phí lắp đặt cho 1 km dây điện trên biển là 50 triệu đồng, còn trên đất liền là 30 triệu đồng.
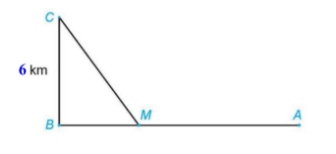
Điểm $M$ trên đoạn $AB$ (điểm nối dây từ đất liền ra đảo) và cách điểm B là bao nhiêu km để tổng chi phí lắp đặt là nhỏ nhất.
Câu 2:
Cho hình chóp tứ giác đều $S.ABCD$ có độ dài tất cả các cạnh bằng 2. Tính thể tích hướng $\overrightarrow{BS.CD}$
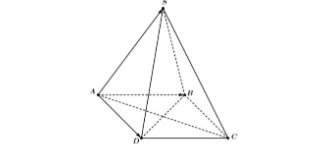
Câu 3:
Từ một tấm bia hình vuông $ABCD$ có cạnh 40 cm, người ta cắt bỏ bốn tam giác cân bằng nhau là $AMB, BNC, CPD$ và $DQA$. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của hình chóp xấp xỉ bằng bao nhiêu để thể tích của nó là lớn nhất (làm tròn đến hàng phần chục)
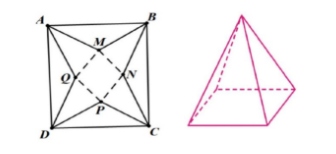
Câu 4:
Một hộ làm nghề dệt vải lụa tơ tằm sản xuất mỗi ngày được $x$ mét vải lụa $(1 \leq x \leq 18)$. Tổng chi phí sản xuất $x$ mét vải lụa, tính bằng nghìn đồng, cho bởi hàm chi phí: $C(x) = x^3 – 3x^2 – 20x + 500$.
Giá sử hộ làm nghề dệt này bán hết sản phẩm mỗi ngày với giá 409nghìn đồng/mét. Hỏi hộ cần sản xuất và bán ra mỗi ngày bao nhiêu mét vải lụa để thu được lợi nhuận tối đa?
Câu 5:
Nồng độ $C$ của một loại hóa chất trong máu sau $t$ giờ tiêm vào có thể được cho bởi công thức $C(t) = \frac{5t}{50 + t^2}$ với $t \geq 0$. Sau khoảng bao nhiêu giờ tiêm thì nồng độ của hóa chất trong máu là cao nhất? (Làm tròn kết quả đến hàng phần trăm)
Câu 6:
Trong không gian $(Oxyz)$, cho $\vec{a}$ và $\vec{b}$ thỏa mãn $|\vec{a}| = 6$, $|\vec{b}| = 5$ và $(\vec{a}, \vec{b}) = 90°$. Tính giá trị gần đúng của $|\vec{a} + \vec{b}|$. (Làm tròn kết quả đến hàng phần trăm)

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh

