Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
A) PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Câu 1:
Cho hàm số $y = f(x)$ có bảng biến thiên như hình bên. Hàm số đồng biến trên khoảng nào dưới đây?
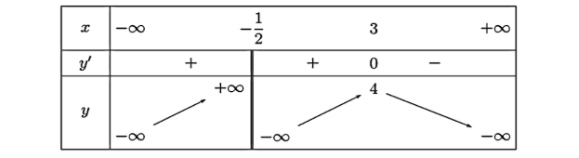
A. $\left(-\frac{1}{2}; 3\right)$
B. $\left(-\frac{1}{2}; +\infty\right)$
C. $(-1; 1)$
D. $\left(-\infty; \frac{1}{2}\right)$
Câu 2:
Cho hàm số $y = f(x)$ có bảng biến thiên như sau:
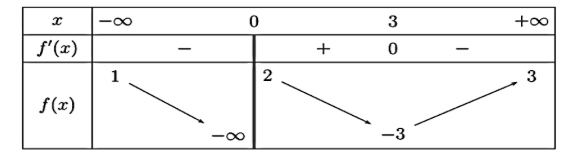
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
A. 1
B. 3
C. 2
D. 4
Câu 3:
Cho hàm số $y = f(x)$ có đồ thị là đường cong như hình bên. Hàm số nghịch biến trên khoảng nào dưới đây?
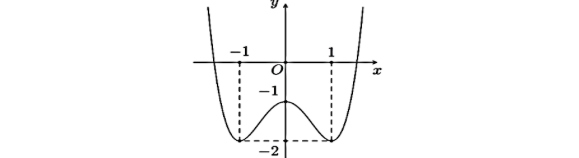
A. $(-\infty; 0)$
B. $(0; 1)$
C. $(1; +\infty)$
D. $(-1; 0)$
Câu 4:
Trong không gian, cho hai hình bình hành $ABCD$ và $MNPQ$ có $O$ và $O’$ tương ứng là giao điểm của hai đường chéo của mỗi hình đó. Khẳng định nào sau đây đúng?
A. $\overrightarrow{AM} + \overrightarrow{BN} + \overrightarrow{CP} + \overrightarrow{DQ} = \overrightarrow{OO’}$
B. $\overrightarrow{AM} + \overrightarrow{BN} + \overrightarrow{CP} + \overrightarrow{DQ} = 2\overrightarrow{OO’}$
C. $\overrightarrow{AM} + \overrightarrow{BN} + \overrightarrow{CP} + \overrightarrow{DQ} = 4\overrightarrow{OO’}$
D. $\overrightarrow{AM} + \overrightarrow{BN} + \overrightarrow{CP} + \overrightarrow{DQ} = \overrightarrow{0}$
Câu 5:
Cho hàm số $y = (x – 2)(x^2 – 5x + 6)$ có đồ thị $(C)$. Mệnh đề nào dưới đây đúng?
A. $(C)$ cắt trục hoành tại ba điểm
B. $(C)$ không cắt trục hoành
C. $(C)$ cắt trục hoành tại một điểm
D. $(C)$ cắt trục hoành tại hai điểm
Câu 6:
Cho hàm số $f(x)$ liên tục trên đoạn $[-1; 3]$ và có đồ thị như hình bên. Gọi $M, m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x)$ trên $[-1; 3]$. Tính $M – m$.
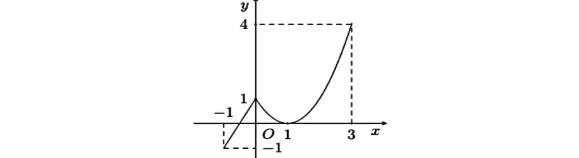
A. 3
B. 5
C. 4
D. 1
Câu 7:
Cho hàm số $f(x)$ có bảng biến thiên như sau:
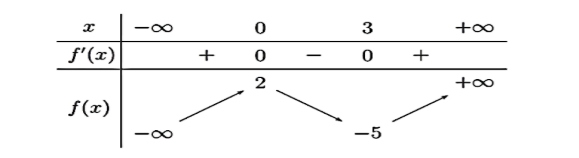
Giá trị cực tiểu của hàm số đã cho bằng
A. 3
B. 2
C. 0
D. $-5$
Câu 8:
Đường cong trong hình bên là đồ thị của hàm số nào trong các hàm số dưới đây?
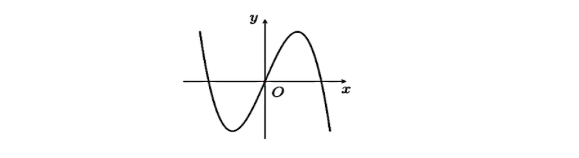
A. $y = -x^3 + 3x$
B. $y = x^4 – x^2 + 1$
C. $y = -x^2 + x + 1$
D. $y = x^3 – 3x$
Câu 9:
Trong không gian, cho hình bình hành $ABCD$ với $A(-2; 3; 1)$, $B(3; 0; -1)$, $C(6; 5; 0)$. Tọa độ đỉnh $D$ là:
A. $(1; 8; -2)$
B. $(11; 2; 2)$
C. $(11; 2; -2)$
D. $(1; 8; 2)$
Câu 10:
Giá trị nhỏ nhất của hàm số $y = x^3 – 3x + 2$ trên đoạn $[0; 2]$ bằng
A. 2
B. 4
C. 1
D. 0
Câu 11:
Cho hàm số $y = f(x)$ liên tục trên $\mathbb{R}$ và có đồ thị $y = f'(x)$ như hình bên. Hàm số $y = f(x)$ có bao nhiêu điểm cực tiểu trên khoảng $\left(-\frac{3}{2}; 5\right)$?
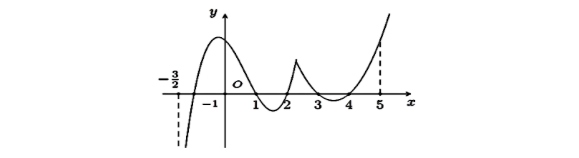
A. 1
B. 3
C. 4
D. 2
Câu 12:
Cho hàm số $y = f(x)$ có bảng biến thiên như sau:
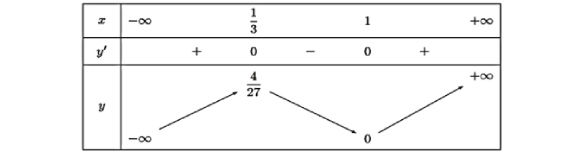
Giá trị cực đại của hàm số đã cho bằng
A. 1
B. $\frac{4}{27}$
C. $\frac{1}{3}$
D. 0
B) PHẦN II. Câu trắc nghiệm đúng sai
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a) b) c) d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1:
Cho hàm số $y = \frac{x^2 – 3x + 3}{x – 1}$. Xét tính đúng, sai các phát biểu sau:
a) Hàm số đạt cực đại tại $x = 0$.
b) Hàm số có tập xác định $D = \mathbb{R} \setminus {1}$.
c) Giá trị lớn nhất của hàm số trên đoạn $\left[-2; \frac{1}{2}\right]$ là $-3$.
d) Đạo hàm của hàm số là $y’ = \frac{x^2 – 2}{(x – 1)^2}$.
Câu 2:
Cho hàm số bậc ba $y = f(x) = ax^3 + bx^2 + cx + d$ có đồ thị như hình vẽ dưới đây:
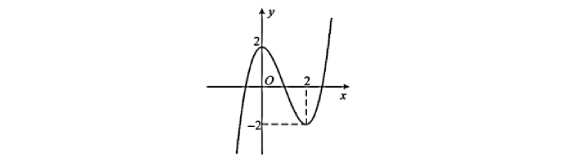
Xét tính đúng, sai của các phát biểu sau:
a) Đường cong trên là đồ thị của hàm số $f(x) = x^3 – 3x^2 + 2$.
b) Có 3 giá trị nguyên của m để phương trình $f(x) = m$ có 3 nghiệm phân biệt.
c) Hàm số đạt cực đại tại $x = 2$.
d) Gọi $M$ và $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f(2\sin x + 1)$ thì $M + m = 5$.
Câu 3:
Trong không gian, cho ba điểm $A(5; 1; 3)$, $B(1; 6; 2)$, $C(5; 0; 4)$. Điểm $D$ thỏa mãn $ABCD$ là hình bình hành. Các khẳng định sau đúng hay sai?
a) Tọa độ của điểm $D$ là $(9; -5; 5)$.
b) Nếu $D(x_0; y_0; z_0)$ thì $\overrightarrow{DC} = (x_0 – 5; y_0; z_0 – 4)$.
c) $\overrightarrow{AB} + \overrightarrow{AD} = 2\overrightarrow{AO}$ (với $O$ là trung điểm $BD$).
d) $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}$.
Câu 4:
Cho hàm số $y = f(x)$ có đồ thị $f'(x)$ là parabol như hình vẽ. Xét tính đúng, sai của mỗi khẳng định sau:
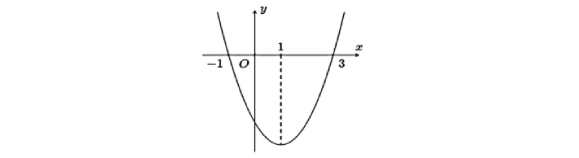
a) $f'(-1) = 0$.
b) Hàm số đồng biến trên $(1; +\infty)$.
c) Hàm số đạt cực tiểu tại $x = -1$.
d) Hàm số nghịch biến trên $(-1; 3)$.
C) PHẦN III. Câu trắc nghiệm trả lời ngắn
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1:
Ba lực $\vec{F_1}$, $\vec{F_2}$, $\vec{F_3}$ cùng tác động vào một vật có phương đối một vuông góc và có độ lớn lần lượt là $2N$, $3N$, $5N$. Hợp lực của ba lực đã cho có độ lớn bao nhiêu Niu-ton (kết quả làm tròn đến một chữ số thập phân).
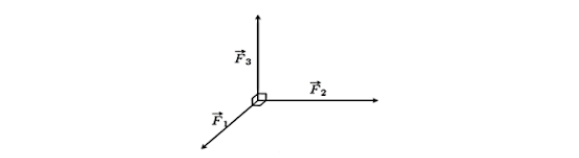
Câu 2:
Có tất cả bao nhiêu giá trị thực của tham số $m$ để đường thẳng $d: y = mx + 1$ cắt đồ thị $(C): y = x^3 – x^2 + 1$ tại 3 điểm $A$, $B(0; 1)$ và $C$ phân biệt sao cho tam giác $AOC$ vuông tại $O$.
Câu 3:
Cho hàm số bậc ba $f(x) = ax^3 + bx^2 + cx + d$ có đồ thị như hình vẽ.
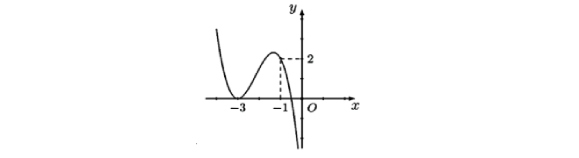
Hỏi đồ thị hàm số $g(x) = \frac{(x^2 + 4x + 3)\sqrt{x^2 + x}}{x[f^2(x) – 2f(x)]}$ có bao nhiêu đường tiệm cận đứng?
Câu 4:
Cho hàm số $y = f(x)$ xác định và có đạo hàm trên $\mathbb{R}$. Biết rằng hàm số $y = f'(3 – 2x)$ có bảng xét dấu như sau:

Hỏi hàm số $y = f(x)$ có bao nhiêu điểm cực đại?
Câu 5:
Cho hàm số $y = f(x)$ có đạo hàm $f'(x) = (x^2 – 1)(x – 4)$ với mọi $x \in \mathbb{R}$. Hàm số $g(x) = f(3 – x)$ đồng biến trên khoảng $(a; b)$ và $(c; +\infty)$. Tính $a + b + c$?
Câu 6:
Ông Bình đặt thợ làm một bể cá, nguyên liệu bằng kính trong suốt, không có nắp đậy dạng hình hộp chữ nhật có thể tích chứa được $220.500 cm^3$ nước. Biết tỉ lệ giữa chiều cao và chiều rộng của bể bằng 3. Xác định diện tích đáy của bể cá để tiết kiệm nguyên vật liệu nhất (Kết quả lấy đơn vị là $m^2$).

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh

