Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1:
Đồ thị hàm số $y = \frac{2x-3}{x-1}$ có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
A. $x = 1$ và $y = -3$
B. $x = 2$ và $y = 1$
C. $x = 1$ và $y = 2$
D. $x = -1$ và $y = 2$
Câu 2:
Đồ thị hàm số nào sau đây không có tiệm cận đứng:
A. $y = \frac{3x-1}{x^2+1}$
B. $y = \frac{-1}{x}$
C. $y = \frac{\sqrt{x+3}}{x+2}$
D. $y = \frac{1}{x^2-2x+1}$
Câu 3:
Giá trị nhỏ nhất của hàm số $y = \frac{x-1}{x+1}$ trên đoạn $[0; 3]$ là:
A. $\min_{[0;3]} y = -3$
B. $\min_{[0;3]} y = \frac{1}{2}$
C. $\min_{[0;3]} y = -1$
D. $\min_{[0;3]} y = 1$
Câu 4:
Cho đồ thị hàm số $y = f(x)$ như hình dưới. Khẳng định nào sau đây là sai?
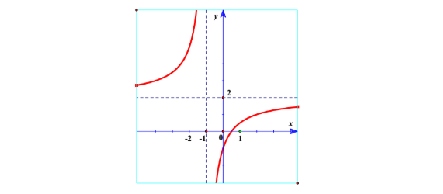
A. Đồ thị hàm số có tiệm cận đứng $x = -1$, tiệm cận ngang $y = 2$
B. Hàm số đồng biến trong khoảng $(-\infty; -1)$ và $(-1; +\infty)$
C. Đồ thị hàm số có hai tiệm cận
D. Hàm số có hai cực trị
Câu 5:
Cho hàm số $y = ax^3 + bx^2 + cx + d$ $(a, b, c, d \in \mathbb{R})$ có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số $a$, $b$, $c$, $d$?
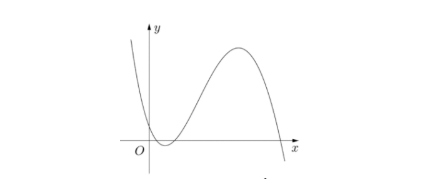
A. 2
B. 1
C. 4
D. 3
Câu 6:
Cho hàm số $y = f(x)$ có bảng biến thiên như sau:
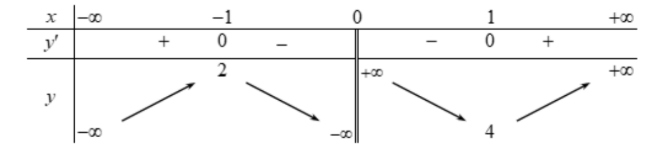
Hàm số nghịch biến trong khoảng nào?
A. $(-1; 1)$
B. $(0; 1)$
C. $(-\infty; 2)$
D. $(4; +\infty)$
Câu 7:
Hàm số nào sau đây có đồ thị là đường cong như hình vẽ bên?
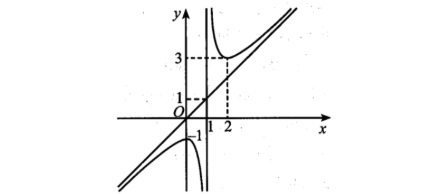
A. $y = x – \frac{1}{x-1}$
B. $y = -x + \frac{1}{x-1}$
C. $y = -x – \frac{1}{x-1}$
D. $y = x + \frac{1}{x-1}$
Câu 8:
Hàm số nào sau đây không có cực trị?
A. $y = 2x + \frac{2}{x+1}$
B. $y = \frac{x+1}{x-2}$
C. $y = x^3 + 3x^2$
D. $y = -x^4 + 2x^2 + 3$
Câu 9:
Cho hàm số $y = f(x)$. Hàm số $y = f'(x)$ có đồ thị như hình vẽ bên. Khẳng định nào sau đây là khẳng định đúng?
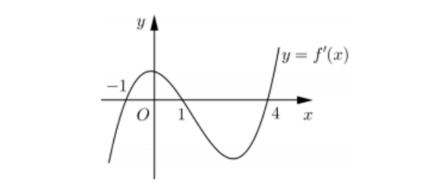
A. Đồ thị hàm số $y = f(x)$ cắt trục hoành tại ba điểm phân biệt
B. Đồ thị hàm số $y = f(x)$ có hai điểm cực trị
C. Đồ thị hàm số $y = f(x)$ có ba điểm cực trị
D. Đồ thị hàm số $y = f(x)$ có một điểm có một điểm cực trị
Câu 10:
Cho tứ diện $ABCD$. Hỏi có bao nhiêu vectơ khác vectơ $\vec{0}$ mà mỗi vectơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện $ABCD$?
A. 4
B. 10
C. 8
D. 12
Câu 11:
Cho tứ diện $ABCD$. Người ta định nghĩa “$G$ là trọng tâm tứ diện $ABCD$ khi $\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} + \overrightarrow{GD} = \vec{0}$”. Khẳng định nào sau đây sai?
A. $G$ là trung điểm của đoạn $IJ$ ($I$, $J$ lần lượt là trung điểm $AB$ và $CD$)
B. $G$ là trung điểm của đoạn thẳng nối trung điểm của $AC$ và $BD$
C. $G$ là trung điểm của đoạn thẳng nối trung điểm của $AD$ và $BC$
D. Chưa thể xác định được
Câu 12:
Cho hình hộp $ABCD.A_1B_1C_1D_1$. Tìm giá trị của $k$ thích hợp điền vào đẳng thức vectơ: $\overrightarrow{AB} + \overrightarrow{B_1C_1} + \overrightarrow{DD_1} = k\overrightarrow{AC_1}$
A. $k = 4$
B. $k = 1$
C. $k = 0$
D. $k = 2$
PHẦN II. Câu trắc nghiệm đúng sai
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1:
Cho hàm số $y = f(x)$ có đồ thị như hình dưới đây.
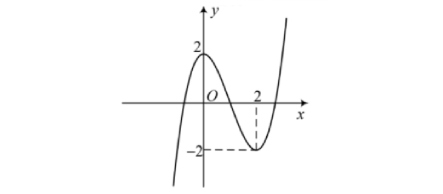
a) Hàm số đã cho đồng biến trên khoảng $(2; +\infty)$.
b) Hàm số đã cho đạt cực đại tại $x = 0$; đạt cực tiểu tại $x = 2$.
c) Trên đoạn $[0; 2]$, giá trị lớn nhất của hàm số đã cho bằng $0$.
d) Phương trình $3f(x) + 4 = 0$ có 3 nghiệm.
Câu 2:
Cho hàm số $y = \frac{x^2 + 3x + 3}{x + 2}$
a) Hàm số đã cho đồng biến trên $(-\infty; -1)$ và $(3; +\infty)$.
b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng $-4$.
c) Đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm $A(0; 1)$.
d) Phương trình tiếp tuyến của đồ thị hàm số đã cho vuông góc với đường thẳng $x – 3y – 6 = 0$ đi qua điểm $B\left(-\frac{3}{2}; \frac{3}{2}\right)$.
Câu 3:
Số dân của một thị trấn sau $t$ năm kể từ năm 1970 được ước tính bởi công thức $f(t) = \frac{26t + 10}{t + 5}$ ($f(t)$ được tính bằng nghìn người).
a) Số dân của thị trấn vào năm 1980 ít hơn 18 nghìn người.
b) Số dân của thị trấn vào năm 1996 ít hơn 26 nghìn người.
c) Xem $f$ là một hàm số xác định trên nửa khoảng $[0; +\infty)$. Vậy hàm số đồng biến trên $[0; +\infty)$
d) Đạo hàm của hàm số $f$ biểu thị tốc độ tăng dân số của thị trấn (tính bằng nghìn người/năm). Vào năm 1998 thì tốc độ tăng dân số là 0,125 nghìn người/năm
Câu 4:
Cho hình lập phương $ABCD.A’B’C’D’$ có cạnh bằng 1.
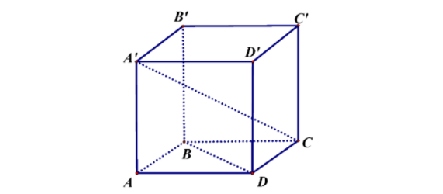
a) $\overrightarrow{BD} = \overrightarrow{B’D’}$.
b) $|\overrightarrow{A’C}| = |\overrightarrow{AC’}| = \sqrt{3}$.
c) $\overrightarrow{A’C} = \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{D’D}$.
d) $\overrightarrow{A’C} \cdot \overrightarrow{BD} = \sqrt{2}$.
Phần III. Câu hỏi trả lời ngắn
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1:
Hàm số $y = \cos 2x + 2x + 1$ trên $[0; \pi]$ có giá trị lớn nhất là $M$, giá trị nhỏ nhất là $m$.
Khi đó $M + m = a\pi + b(a, b \in \mathbb{R})$. Tính $a + b$.
Câu 2:
Giả sử hàm số $f(x) = -x^3 + 12x + 1$ có giá trị cực đại là $a$ và giá trị cực tiểu là $b$
Giá trị của biểu thức $M = 2a – 3b$ bằng bao nhiêu?
Câu 3:
Cho đồ thị hàm số $y = f(x)$ có bảng biến thiên xác định như hình. Biết rằng đồ thị hàm số có tiệm cận đứng $x = x_0$, tiệm cận ngang là $y = y_0$ và $x_0 y_0 = 16$. Hỏi $m$ bằng?
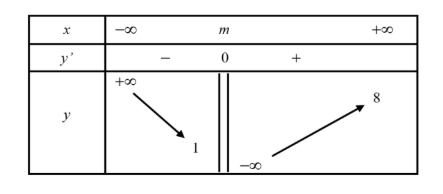
Câu 4:
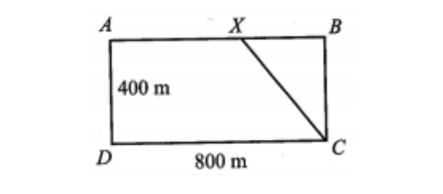
Một vận động viên thể thao hai môn phối hợp luyện tập với một bể bơi hình chữ nhật rộng $400 , m$, dài $800 , m$. Vận động viên chạy phối hợp với bơi như sau: Xuất phát từ điểm $A$, chạy đến điểm $X$ và bơi từ điểm $X$ đến điểm $C$ Hỏi nên chọn điểm $X$ cách $A$ gần bằng bao nhiêu mét để vận động viên đến $C$ nhanh nhất (làm tròn kết quả đến hàng đơn vị)? Biết rằng vận tốc chạy là $30$ km/h, vận tốc bơi là $6$ km/h.
Câu 5:
Cho hình chóp $S.ABC$ có $\overrightarrow{SA} = \vec{a}$, $\overrightarrow{SB} = \vec{b}$, $\overrightarrow{SC} = \vec{c}$ và các điểm $M, N$ lần lượt là trung điểm các cạnh $AB, SC$. Các điểm $P, Q$ nằm trên các đường thẳng $SA, BN$ sao cho $\overrightarrow{PQ} \parallel \overrightarrow{CM}$. Khi biểu diễn véctơ $\overrightarrow{PQ}$ theo ba vectơ $\vec{a}, \vec{b}, \vec{c}$, ta được $\overrightarrow{PQ} = \frac{-m}{n}\vec{a} – \frac{p}{q}\vec{b} + \frac{r}{z}\vec{c}$ (với $\frac{m}{n}, \frac{p}{q}, \frac{r}{z}$ là các phân số tối giản và $m, n, p, q, r, z \in \mathbb{Z}$). Giá trị của biểu thức $\frac{m}{n} + \frac{p}{q} + \frac{r}{z}$ bằng bao nhiêu (làm tròn kết quả đến hàng phần mười)?
Câu 6:
Một tên lửa bay vào không trung với quãng đường đi được là $s(t)$ (km) là hàm phụ thuộc theo biến $t$ (giây) tuân theo biểu thức sau: $s(t) = e^{t+3} + 2te^{3t+1}$ (km). Vận tốc của tên lửa sau 1 giây là $me^r$ (km/s). Tính $T = m + n$ (Biết hàm biểu thị vận tốc là đạo hàm cấp một của hàm biểu thị quãng đường theo thời gian)?

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh