PHẦN I (3 điểm): Câu hỏi trắc nghiệm nhiều phương án lựa chọn

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1:

Cho mệnh đề chứa biến $P(x): “x + 1 > 3″$. Chọn mệnh đề ĐÚNG.

A. $P(2)$
B. $P(-10)$
C. $P(0)$
D. $P(7)$

Câu 2:

Mệnh đề $P(x): “\forall x \in \mathbb{N}, x^2 – x + 7 = 0″$. Phủ định của mệnh đề $P$ là

A. $\exists x \in \mathbb{N}, x^2 – x + 7 > 0$
B. $\forall x \in \mathbb{N}, x^2 – x + 7 > 0$
C. $\forall x \in \mathbb{N}, x^2 – x + 7 \geq 0$
D. $\exists x \in \mathbb{N}, x^2 – x + 7 \neq 0$

Câu 3:

Sử dụng các kí hiệu đoạn, khoảng, nửa khoảng để viết tập hợp $A = {x \in \mathbb{R} | -4 \leq x < 9}$ ta được

A. $A = [-4; 9)$
B. $A = (-4; 9]$
C. $A = [-4; 9]$
D. $A = (-4; 9)$

Câu 4:

Cho hai tập hợp $A = {0; 2; 3; 5}$ và $B = {2; 7}$. Khi đó $A \cap B$ là

A. $A \cap B = {2; 5}$
B. $A \cap B = {2}$
C. $A \cap B = \emptyset$
D. $A \cap B = {0; 2; 3; 5; 7}$

Câu 5:

Một lớp có 45 học sinh. Mỗi em đều đăng ký chơi ít nhất một trong hai môn: bóng đá và bóng chuyền. Có 35 em đăng ký môn bóng đá, 15 em đăng ký môn bóng chuyền. Hỏi có bao nhiêu em đăng ký chơi cả 2 môn?

A. 5
B. 10
C. 30
D. 25

Câu 6:

Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?

A. $-2x + y \leq 3$
B. $x^2 – 4y > 0$
C. $2x + 5y > 3z$
D. $\frac{2}{x} + 3y < 5$

Câu 7:

Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình $\begin{cases} x + y – 2 \leq 0 \ 2x – 3y + 2 > 0 \end{cases}$?

A. $(0, 0)$
B. $(1, 1)$
C. $(-1, 1)$
D. $(-1, -1)$

Câu 8:

Giá trị của $\cos 30° + \sin 60°$ bằng bao nhiêu?

A. $\sqrt{3}$
B. $1$
C. $\frac{\sqrt{3}}{2}$
D. $\frac{\sqrt{3}}{3}$

Câu 9:

Xét tam giác $ABC$ tùy ý, đường tròn ngoại tiếp tam giác có bán kính $R$, $BC = a$. Mệnh đề nào dưới đây đúng?

A. $\frac{a}{\sin A} = 4R$
B. $\frac{a}{\sin A} = R$
C. $\frac{a}{\sin A} = 3R$
D. $\frac{a}{\sin A} = 2R$

Câu 10:

Tam giác $ABC$ có $\hat{B} = 60°$, $\hat{C} = 45°$, $AB = 3$. Độ dài cạnh $AC$ là

A. $\frac{3\sqrt{6}}{2}$
B. $\sqrt{6}$
C. $\frac{3\sqrt{2}}{2}$
D. $\frac{2\sqrt{6}}{3}$

Câu 11:

Hai vectơ được gọi là bằng nhau nếu

A. Chúng có cùng hướng và cùng độ dài.
B. Chúng có hướng ngược nhau và cùng độ dài.
C. Chúng có cùng độ dài.
D. Chúng có cùng phương và cùng độ dài.

Câu 12:

Cho ba điểm $M, N, P$ thẳng hàng như hình vẽ.

Khi đó các cặp vectơ nào sau đây ngược hướng?

A. $\overrightarrow{MN}; \overrightarrow{NP}$
B. $\overrightarrow{NM}; \overrightarrow{PM}$
C. $\overrightarrow{MN}; \overrightarrow{PN}$
D. $\overrightarrow{MP}; \overrightarrow{NP}$

PHẦN 2 (4 điểm): Câu trắc nghiệm đúng sai

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1:

Cho các tập hợp $A = {x \in \mathbb{N} | x \leq 3}$, $B = {-3; -1; 0; 1}$, $C = {x \in \mathbb{R} | 3x + 1 < 0}$.

a) $3 \in \mathbb{N}$.

b) $A = {1; 2; 3}$.

c) $A \subset B$.

d) $C = \emptyset$.

Câu 2:

Cho tập hợp $A = {x \in \mathbb{R} | (x^2 – 3x + 2)(x – 3) = 0}$, $B = {1; 3; 4}$, $E = [-5; 1]$, $D = (-3; 2)$.

a) Tập hợp $A \cup B$ có 6 phần tử.

b) $E \cap D = (-3; 1]$.

c) $C_{\mathbb{R}} E = (-\infty; -5) \cup (1; +\infty)$.

d) Tập hợp $\mathbb{Z} \cap D$ có 5 phần tử.

Câu 3:

Cho tam giác $ABC$, biết $b = 6$, $c = 5$, $A = 60°$.

a) Bán kính $R$ của đường tròn ngoại tiếp tam giác $ABC$ là $R = \frac{b}{2\sin B}$.

b) $S = 15\sqrt{3}$.

c) $a = \sqrt{31}$.

d) $\sin A = \frac{1}{2}$.

Câu 4:

Một công ty điện tử sản xuất hai kiểu radio trên hai dây chuyền độc lập. Radio kiểu một sản xuất trên dây chuyền một với công suất 45 radio/ngày, radio kiểu hai sản xuất trên dây chuyền hai với công suất 80 radio/ngày. Để sản xuất một chiếc radio kiểu một cần 12 linh kiện, để sản xuất một chiếc radio kiểu hai cần 9 linh kiện. Tiền lãi khi bán một chiếc radio kiểu một là 250 000 đồng, lãi thu được khi bán một chiếc radio kiểu hai là 180 000 đồng. Gọi $x$ và $y$ lần lượt là số radio kiểu một và số radio kiểu hai mà công ty này sản xuất trong một ngày ($x, y \in \mathbb{N}^*$). Biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là 900.

a) Số tiền lãi mà công ty này thu về hàng ngày là $f(x; y) = 250000x + 180000y$ (đồng).

b) Số linh kiện để sản xuất hai kiểu radio là $9x + 12y$.

c) Miền nghiệm của hệ bất phương trình thỏa mãn tất cả các điều kiện của bài toán là một tứ giác.

d) Công ty thu lợi nhuận cao nhất khi sản xuất 45 radio kiểu một và 40 radio kiểu hai.

PHẦN 3 (3 điểm): Tự luận

Câu 1:

(0,5 điểm) Liệt kê các phần tử của tập hợp $S = {x \in \mathbb{N} | 3x^2 – x – 2 = 0}$.

Câu 2:

(0,5 điểm) Cho các tập hợp $A = (-\infty; 0]$; $B = (1; +\infty)$; $C = [0; 1]$. Xác định tập hợp $(A \cup B) \cap C$.

Câu 3:

(1 điểm) Biểu diễn miền nghiệm của bất phương trình $x + 2y \leq 6$.

Câu 4:

(0,5 điểm) Cho tam giác $ABC$ có các cạnh: $AB = 5$, $BC = 7$, $CA = 10$. Tính diện tích tam giác $ABC$.

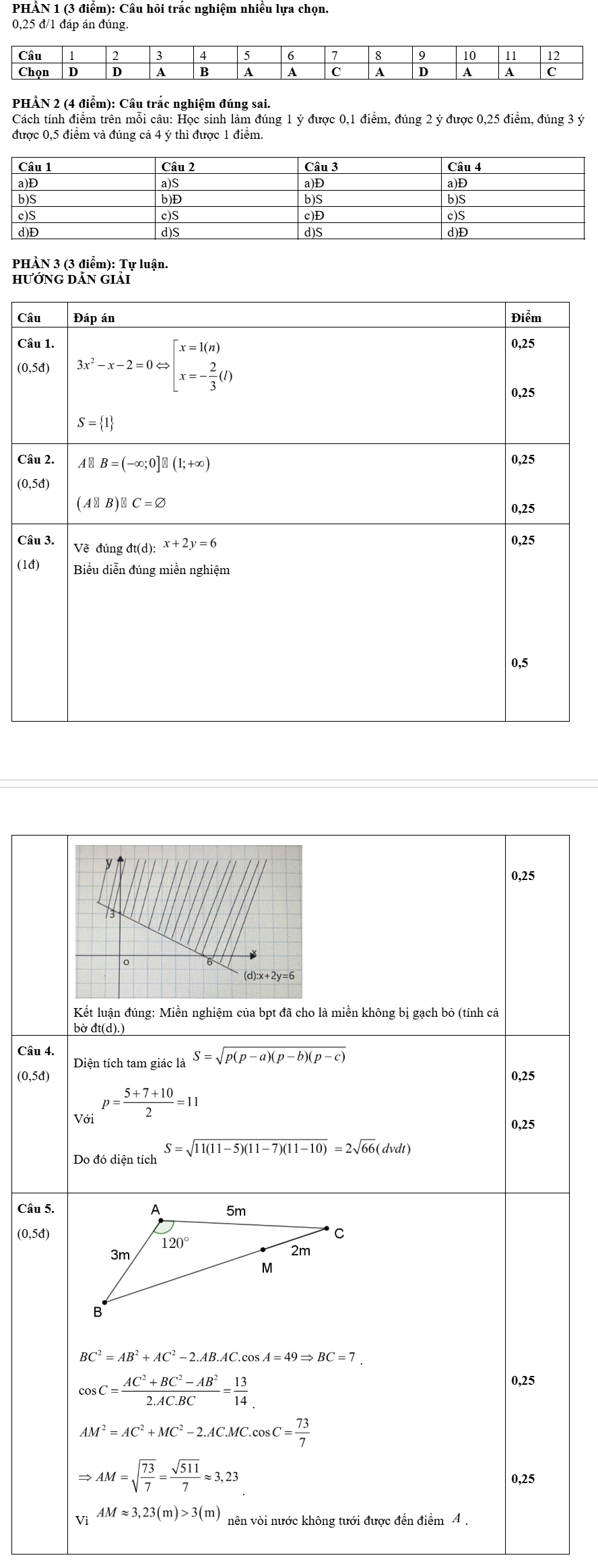
Câu 5:

(0,5 điểm) Ông Minh có một mảnh vườn hình tam giác có các kích thước như hình vẽ. Tại điểm $M$ nằm trong đoạn thẳng $BC$ và cách $C$ một khoảng bằng 2 mét, ông Minh dự định lắp một vòi tưới nước dạng tòa trồn bán kính 3 mét (tức là vòi tưới nước này có thể tưới nước cho một khu vực đất có dạng hình tròn nhận vòi tưới nước là tâm và có bán kính 3 mét).

Hỏi vòi tưới nước này có thể tưới nước đến được vị trí $A$ của khu vườn hay không? Vì sao?

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh