Phần 1: Trắc nghiệm đáp án

Câu 1:

Cho hàm số $f(x)$ có bảng biến thiên như sau:

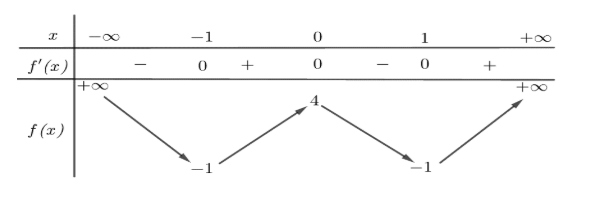
Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. $(-\infty; -1)$
B. $(0; 1)$
C. $(-1; 1)$
D. $(-1; 0)$

Câu 2:

Cho hàm số $f(x)$, bảng xét dấu của $f'(x)$ như sau:

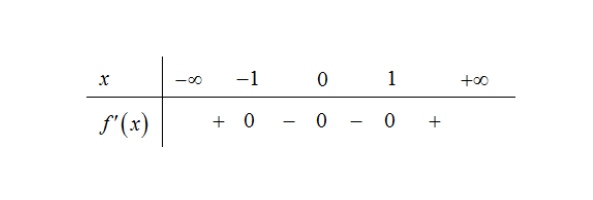
Số điểm cực trị của hàm số đã cho là

A. 0
B. 2
C. 1
D. 3

Câu 3:

Cho hàm số $f(x)$ có bảng biến thiên của hàm số $f'(x)$ như hình vẽ.

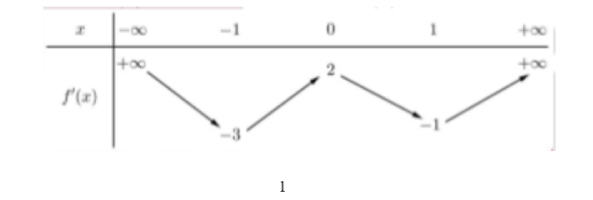
Số điểm cực trị của hàm số đã cho là

A. 3
B. 2
C. 1
D. 4

Câu 4:

Giá trị lớn nhất của hàm số $f(x) = x^3 – 3x + 2$ trên đoạn $[-1; 3]$ bằng

A. 4
B. 2
C. 20
D. 16

Câu 5:

Cho hàm số $y = f(x)$ xác định và liên tục trên $(-4; 4)$ và có bảng biến thiên trên $(-4; 4)$ như sau

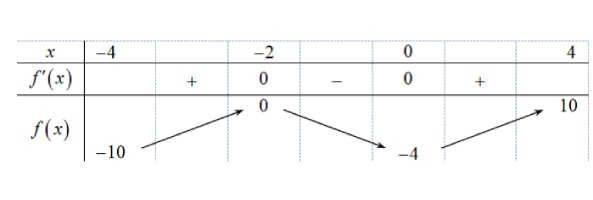
Mệnh đề nào sau đây đúng?

A. $\min_{(-4; 4)} y = -4$ và $\max_{(-4; 4)} y = 10$
B. Hàm số không có GTLN, NN trên $(-4; 4)$
C. $\max_{(-4; 4)} y = 10$ và $\min_{(-4; 4)} y = -10$
D. $\max_{(-4; 4)} y = 0$ và $\min_{(-4; 4)} y = -4$

Câu 6:

Đường tiệm cận đứng của đồ thị hàm số $y = \frac{3x + 1}{x – 5}$ là

A. $x = 3$
B. $y = 3$
C. $x = 5$
D. $y = 5$

Câu 7:

Đường thẳng $y = 2$ là tiệm cận ngang của đồ thị hàm số

A. $y = \frac{3x + 1}{x – 2}$
B. $y = \frac{4x + 5}{2x + 1}$
C. $y = \frac{4 – 2x}{x – 1}$
D. $y = \frac{5x + 2}{2x – 1}$

Câu 8:

Đường tiệm cận xiên của đồ thị hàm số $y = \frac{2x^2 + x – 2}{x + 1}$ là

A. $y = 2$
B. $y = 2x – 1$
C. $y = -1$
D. $y = 2x + 1$

Câu 9:

Đường cong trong hình bên dưới là đồ thị của hàm số nào trong bốn hàm số dưới đây?

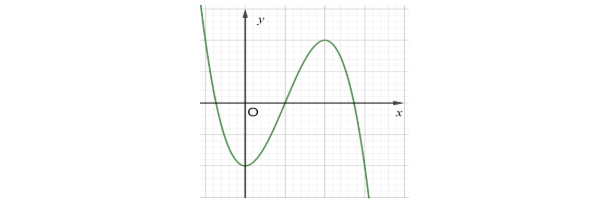
A. $y = x^3 – 3x^2 + 2$
B. $y = -x^3 + 3x + 2$
C. $y = -x^3 + 3x^2 – 2$
D. $y = x^3 – 3x + 2$

Câu 10:

Đồ thị sau đây là của hàm số nào?

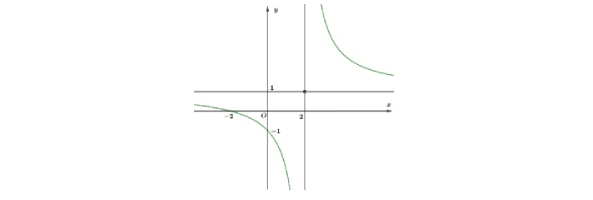
A. $y = \frac{2x + 1}{x – 1}$
B. $y = \frac{x + 2}{x – 2}$
C. $y = \frac{x + 2}{x + 1}$
D. $y = \frac{x – 1}{x + 1}$

Câu 11:

Đồ thị trong hình bên dưới là đồ thị của hàm số

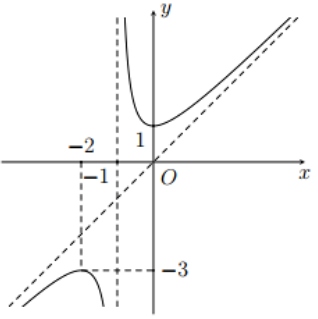
A. $y = x – \frac{1}{x + 1}$
B. $y = \frac{2x + 1}{x + 1}$
C. $y = \frac{x^2 – x + 1}{x + 1}$
D. $y = \frac{x^2 + x + 1}{x + 1}$

Câu 12:

Một doanh nghiệp dự kiến lợi nhuận khi sản xuất $x$ sản phẩm ($0 \leq x \leq 200$) được cho bởi hàm số $y = -x^3 + 150x^2$ (đơn vị: đồng). Hỏi doanh nghiệp cần sản xuất bao nhiêu sản phẩm để đạt được lợi nhuận cao nhất?

A. 50
B. 150
C. 75
D. 100

Phần 2. Trắc nghiệm lựa chọn đúng sai

Thí sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 13:

Cho hàm số $y = f(x)$ có bảng biến thiên

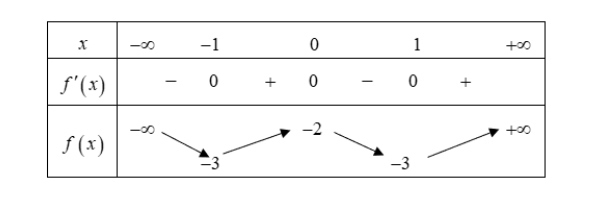
Các khẳng định dưới đây đúng hay sai?

a) Hàm số đồng biến trên khoảng $(-1; 0) \cup (1; +\infty)$.

b) Hàm số nghịch biến trên khoảng $(-\infty; -2)$.

c) Hàm số có 3 điểm cực trị.

d) Giá trị $m^3 x_{CD} + m x_{CT} – 1 = 0$ khi và chỉ khi $\begin{cases} m = -1 \ m = -\frac{1}{2} \end{cases}$.

Câu 14:

Cho hàm số $y = \frac{x – 2}{x + m}$ ($m$ tham số)

a) Khi $m = 1$, đồ thị hàm số có tiệm cận đứng $x = 1$

b) Đồ thị hàm số có tiệm cận ngang $y = 1$

c) Với mọi $m \in \mathbb{R}$, đồ thị hàm số có tiệm cận ngang $y = 1$ và tiệm cận đứng $x = -m$

d) Với $m = -2$, đồ thị hàm số có hai đường tiệm cận.

Câu 15:

Cho hàm số $y = f(x)$ xác định trên $\mathbb{R} \setminus {-2}$ và có bảng biến thiên như sau:

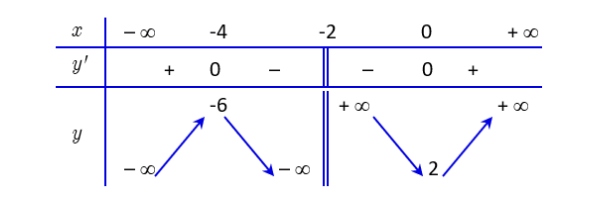
Xét tính đúng sai của các mệnh đề sau

a) Hàm số có giá trị cực tiểu bằng 2.

b) $x = -2$ là đường tiệm cận đứng của đồ thị hàm số.

c) Hàm số không có giá trị lớn nhất trên $[-5; -3]$.

d) Biết hàm số $f(x)$ có dạng $f(x) = \frac{ax^2 + bx + c}{x + n}$ khi đó $f(1) = \frac{5}{3}$

Câu 16:

Gia sư một hạt chuyển động trên một trục thẳng đứng chiều dương hướng lên trên sao cho tọa độ của hạt (đơn vị: mét) tại thời điểm $t$ (giây) là $y = t^3 – 12t + 3, t \geq 0$

Các mệnh đề sau đúng hay sai?

a) Vận tốc của hạt khi chuyển động: $v(t) = 3t^2 – 12, t \geq 0$.

b) Hạt chuyển động xuống dưới khi $t > 2$.

c) Quãng đường hạt đi được trong khoảng thời gian $0 \leq t \leq 3$ là $9m$.

d) Khi $t \geq 0$ thì hạt tăng tốc.

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn

Thí sinh trả lời từ câu 17 đến câu 22

Câu 17:

Cho hàm số $y = f(x)$ có bảng biến thiên

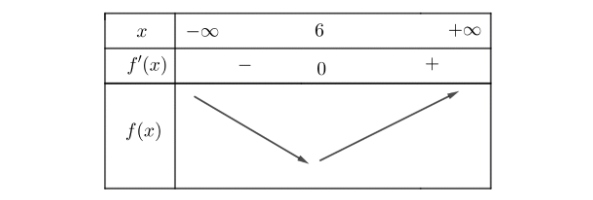
Biết hàm số $y = f\left(\frac{1}{2}x^2 + 3x + 6\right)$ nghịch biến trên khoảng $(a; b)$, với $a, b$ là các số thực. Tính $S = a + b$?

Câu 18:

Cho hàm số $y = f(x)$ có đạo hàm $f'(x) = (x^2 – x)(x^2 – 4x + 3), \forall x \in \mathbb{R}$. Tìm tổng tất cả các giá trị nguyên của tham số $m$ để hàm số $g(x) = f(x^2 + m)$ có 3 điểm cực trị.

Câu 19:

Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình bên dưới. Biết hàm số $y = |f(x)|$ đạt giá trị lớn nhất trên đoạn $[-1; 4]$ tại điểm $A(a; b)$

Giá trị của $S = \log_a b$ bằng bao nhiêu? (Làm tròn đến hàng phần trăm).

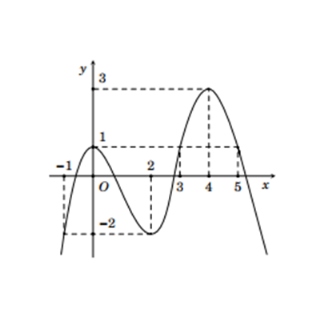
Câu 20:

Cho hàm số $y = f(x)$ xác định, liên tục trên đoạn $[-2; 2]$ và có đồ thị là đường cong trong hình vẽ bên dưới. Có bao nhiêu giá trị của tham số $m$ thuộc khoảng $(-10; 10)$ để phương trình $f(|x|) = m$ có 4 nghiệm phân biệt?

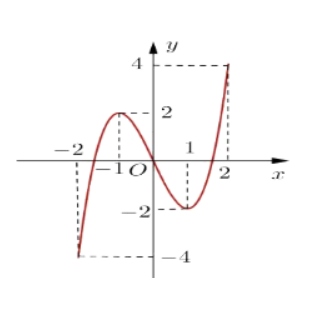
Câu 21:

Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số hàm số $y = \frac{2x^2 – 3x + 3}{x + 1}$ có dạng $y = ax + b$. Khi đó $a + b$ bằng ………………

Câu 22:

Ông A có một khu đất hình elip với độ dài trục lớn $10m$ và độ dài trục bé $8m$. Ông A muốn chia khu đất thành hai phần, phần thứ nhất là một hình chữ nhật nội tiếp elip dùng để xây bể cá cảnh và phần còn lại dùng để trồng hoa. Biết chi phí xây bể cá là $800.000$ đồng trên $1m^2$ và chi phí trồng hoa là $900.000$ đồng trên $1m^2$. Hỏi ông A có thể thiết kế xây dựng như trên với tổng chi phí thấp nhất là bao nhiêu triệu đồng (kết quả làm tròn đến hàng phần trăm)?

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh