Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Câu 1:
Cho hàm số $f(x)$ có bảng biến thiên như sau:
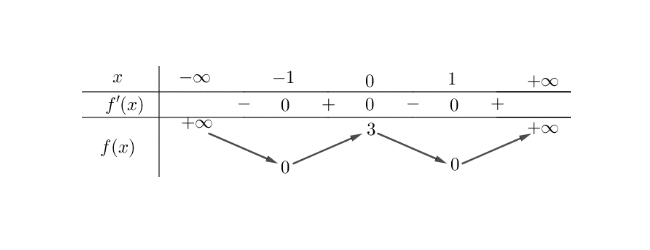
Hàm số đã cho đồng biến trên khoảng nào sau đây?
A. $(-\infty; -1)$
B. $(0; 1)$
C. $(-1; 0)$
D. $(-1; +\infty)$
Câu 2:
Cho hàm số $y = f(x)$ có bảng biến thiên như sau:
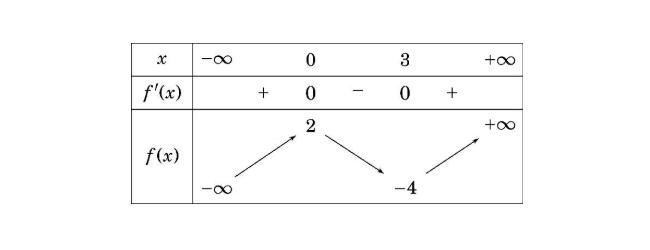
Giá trị cực tiểu của hàm số đã cho bằng
A. 2
B. 3
C. 0
D. -4
Câu 3:
Cho hàm số $y = f(x)$ có bảng biến thiên trên $[-5; 7]$ như sau
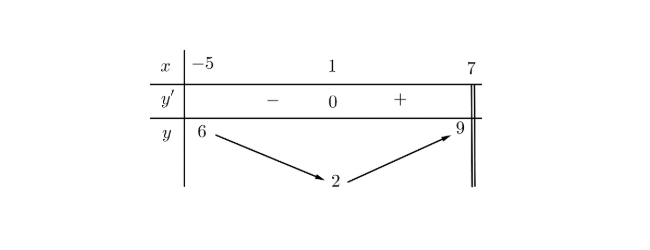
Mệnh đề nào dưới đây đúng?
A. $\min_{[-5;7]} f(x) = 6$
B. $\min_{[-5;7]} f(x) = 2$
C. $\max_{[-5;7]} f(x) = 9$
D. $\max_{[-5;7]} f(x) = 6$
Câu 4:
Trên đoạn $[0; 3]$, hàm số $y = -x^3 + 3x$ đạt giá trị lớn nhất tại điểm
A. $x = 0$
B. $x = 3$
C. $x = 1$
D. $x = 2$
Câu 5:
Tiệm cận ngang của đồ thị hàm số $y = \frac{x – 2}{x + 1}$ là:
A. $x = -1$
B. $x = 1$
C. $y = -1$
D. $y = 1$
Câu 6:
Tiệm cận đứng của đồ thị hàm số $y = \frac{-x + 2}{x + 2}$.
A. $x = 2$
B. $x = -2$
C. $y = -1$
D. $y = -2$
Câu 7:
Đường cong ở hình bên dưới là đồ thị của hàm số nào?
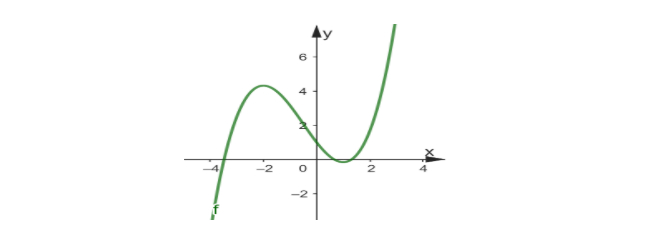
A. $y = x^3 – 2x$
B. $y = -x^3 + 3x^2 – 2$
C. $y = \frac{1}{3}x^3 + \frac{1}{2}x^2 – 2x + 1$
D. $y = -\frac{1}{3}x^3 + \frac{1}{2}x^2 + 2$
Câu 8:
Hàm số nào có bảng biến thiên như hình dưới đây?
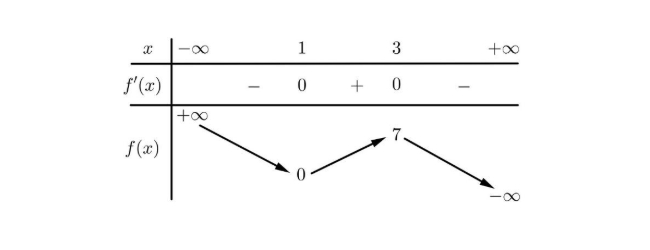
A. $y = -\frac{7}{4}x^3 + \frac{21}{2}x^2 – \frac{63}{4}x + 7$
B. $y = \frac{7}{4}x^3 + \frac{21}{2}x^2 – \frac{63}{4}x + 7$
C. $y = -\frac{5}{3}x^3 + \frac{21}{2}x^2 – \frac{63}{4}x$
D. $y = \frac{5}{3}x^3 + \frac{21}{2}x^2 – \frac{63}{4}x$
Câu 9:
Cho hình hộp $ABCD.MNPQ$ như hình vẽ sau:
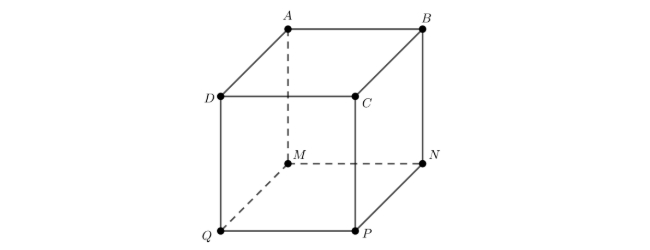
Khi đó $\overrightarrow{AM} + \overrightarrow{AB} + \overrightarrow{AD}$ bằng
A. $\overrightarrow{PA}$
B. $\overrightarrow{AP}$
C. $\overrightarrow{AC}$
D. $\overrightarrow{CA}$
Câu 10:
Trong không gian với hệ trục tọa độ $Oxyz$, gia sư $\vec{p} = 4\vec{k} + 2\vec{j} – 20\vec{i}$ khi đó $\vec{p}$ có tọa độ là
A. $(-20; 2; 4)$
B. $(4; 2; -20)$
C. $(4; 2; 20)$
D. $(2; 4; -20)$
Câu 11:
Cho hàm số $f(x) = \frac{1}{2}x^3 + (m – 2024)x^2 – \frac{3}{2}x + 2$ ($m$ là tham số thực). Để đồ thị hàm số $f(x)$ có tâm đối xứng nằm trên trục $Oy$ thì giá trị của tham số $m$ bằng
A. 2
B. 1012
C. 2024
D. 2026
Câu 12:
Cho hình hộp chữ nhật $ABCD.EFGH$ có các cạnh $FB = 2$, $AD = 3$, $CD = 4$. Chọn hệ trục tọa độ $Oxyz$ có đỉnh $F$ trùng với gốc tọa độ $O$; các điểm $E, G, B$ lần lượt nằm trên các tia $Ox, Oy, Oz$ sao cho các vecto $\overrightarrow{FE}, \overrightarrow{FG}, \overrightarrow{FB}$ lần lượt cùng hướng với $\vec{i}, \vec{j}, \vec{k}$. Gọi $M$ là trung điểm của cạnh $DH$. Tọa độ của vecto $\overrightarrow{FM}$ là
A. $(4; 3; 1)$
B. $(8; 6; 2)$
C. $(8; 3; 2)$
D. $\left(\frac{2}{3}; 1; \frac{8}{3}\right)$
Phần 2. Trắc nghiệm lựa chọn đúng sai
Thí sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a) b) c) d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13:
Cho hàm số $y = f(x)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:
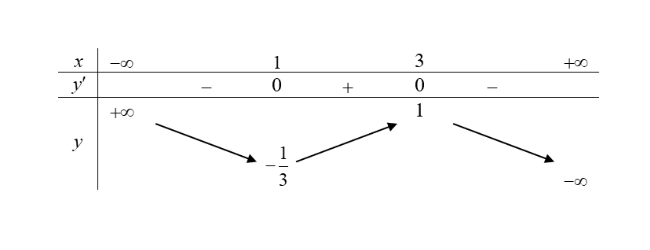
a) Hàm số đồng biến trên khoảng $(-1; 3)$
b) $x = 1$ là điểm cực đại của hàm số.
c) Hàm số nghịch biến trên khoảng $(4; 5)$
d) Đường thẳng $x = 1$ là một đường tiệm cận đứng của đồ thị hàm số.
Câu 14:
Cho hàm số $y = f(x) = \frac{m^2x – 1}{x + 1}$.
a) $y’ = \frac{m^2 + 1}{(x + 1)^2}$ với $x \neq -1$.
b) Với $m = 1$, hàm số đạt giá trị lớn nhất trên đoạn $[1; 2]$ là 0.
c) Giá trị lớn nhất của hàm số $y = f(x) = \frac{m^2x – 1}{x + 1}$ trên đoạn $[1; 2]$ là $f(0)$.
d) Tổng tất cả các giá trị thực của $m$ để giá trị nhỏ nhất của hàm số $y = f(x) = \frac{m^2x – 1}{x + 1}$ trên đoạn $[1; 2]$ bằng 4 là 3.
Câu 15:
Cho hàm số $y = f(x) = ax^3 + bx^2 + cx + d$ $(a \neq 0)$ và có đồ thị là đường cong như hình bên
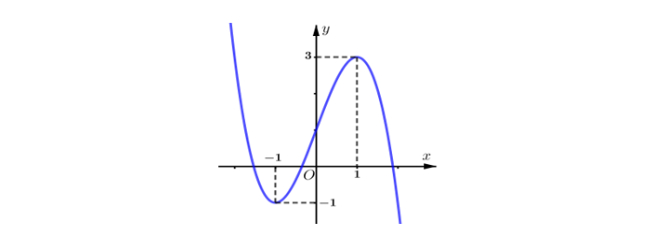
a) Hệ số $a < 0$.
b) Đồ thị hàm số $y = f(x)$ có điểm cực tiểu là $(1; 3)$
c) Hàm số đồng biến trên khoảng $(-1; 1)$.
d) $f(3) = -5$.
Câu 16:
Trong không gian với hệ tọa độ $Oxyz$ cho điểm $M(3; -5; 4)$ và $\overrightarrow{OM} = (x; y; z)$. Các khẳng định sau đúng hay sai?
a) Ta có: $\begin{cases} x = 3 \ y = 5 \ z = 4 \end{cases}$
b) $x + 2y + z = -11$.
c) $\sqrt{x^2 + y^2 + z^2} = 5\sqrt{2}$.
d) Gọi $H$ là hình chiếu vuông góc của điểm $M$ lên $mp(Oxy)$, khi đó: $H(3; 5; 0)$.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn
Thí sinh trả lời từ câu 17 đến câu 22
Câu 17:
Có bao nhiêu giá trị nguyên của $m \in [-15; 10]$ để hàm số $y = \ln(x^2 + 1) – mx – 5$ nghịch biến trên khoảng $(0; +\infty)$?
Câu 18:
Hằng ngày mực nước của một hồ thủy điện lên và xuống theo lượng nước mưa và các suối nước để vệ hồ. Tính từ thời điểm 8 giờ sáng, độ sâu của mực nước trong hồ tính theo mét và là xuống theo thời gian $t$ (giờ) trong ngày cho bởi công thức $h(t) = -\frac{1}{3}t^3 + 5t^2 + 24t (t > 0)$. Biết rằng phải thông báo cho nhân dân phải di dời trước khi và nước theo quy định trước 5 giờ. Hỏi cần thông báo cho người dân di dời trước khi và nước theo quy định trước khi và nước mấy giờ.
Câu 19:
Một cửa hàng bán được 2.000 cái tivi mỗi năm. Để bán được số tivi đó, của hàng đặt hàng từ Nhà máy sản xuất thành nhiều lần trong năm, số tivi đặt cho mỗi máy là như nhau cho các lần đặt hàng. Mỗi lần lấy hàng từ nhà máy về cửa hàng chủ để trung bày được một nửa, một nửa số hàng còn lại phải lưu kho. Chi phí gửi trong kho là 100.000 đồng một cái. Đặt mỗi hàng chi phí cố định là 3.000.000 đồng mỗi cái. Hàm tổng chi phí cửa hàng phải trả là $f(x)$ với $x$ là số tivi mà cửa hàng đặt mỗi lần. Hàm $f(x)$ có tiệm cận xiên dạng $y = ax + b$. Tính giá trị của biểu thức $T = \frac{b}{a}$?
Câu 20:
Cho hàm số bậc ba $f(x) = ax^3 + bx^2 + cx + d (a \neq 0)$ có đồ thị như hình vẽ sau
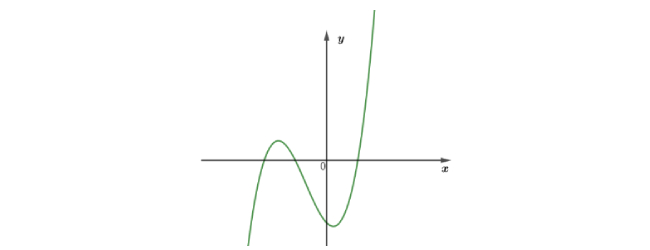
Trong các số thực $a; b; c; d$ có bao nhiêu số dương?
Câu 21:
Một chiếc đèn trang trí được thiết kế với địa đèn được giữ bởi ba đoàn dây cáp $SA$, $SB$, $SC$ biết $SA = SB = SC$ và địa đèn được giữ bởi cáo sợi dây cáp tại các điểm $A, B, C$ sao thành tam giác đều. Góc tạo bởi các sợi dây cáp và địa đèn bằng $60°$, độ lớn lực căng của ba sợi dây cáp là $5N$. Độ lớn của trọng lực $\vec{P}$ tác động lên chiếc đèn bằng $\frac{a\sqrt{3}}{b}N$. $a, b$ là các số nguyên dương, $b$ là phân số tối giản. Tìm tổng $a + b$.
Câu 22:
Ba chiếc máy bay không người lái cùng bay lên tại một địa điểm. Sau một thời gian bay, chiếc máy bay thứ nhất cách điểm xuất phát về phía Đông $40(km)$ và về phía Nam $60(km)$, đông thời cách mặt đất $3(km)$. Chiếc máy bay thứ hai cách điểm xuất phát về phía Bắc $90(km)$ và về phía Tây $50(km)$, đông thời cách mặt đất $6(km)$. Chiếc máy bay thứ ba đang trong quá trình bay thì đột ngột mất tín hiệu, biết rằng lần cuối (trước khi mất tín hiệu) máy bay thứ nhất xác định được khoảng cách giữa máy bay thứ nhất và máy bay thứ ba là $2\sqrt{3401}(km)$ và máy bay thứ ba năm giữa máy bay thứ nhất và thứ hai, đồng thời ba chiếc máy bay này thẳng hàng. Em hãy xác định khoảng cách từ vị trí xuất phát đến lúc máy bay số ba bị mất tín hiệu.


ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh

