Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.

Câu 1:

Cho hàm số $y = f(x)$ có đạo hàm $f'(x) = \frac{-2024x}{(x-2)^2}$. Số điểm cực tiểu của hàm số $y = f(x)$ là

A. 1
B. 3
C. 2
D. 0

Câu 2:

Cho hàm số $y = f(x)$ có đạo hàm $f'(x) = 4 – x^2, \forall x \in \mathbb{R}$. Khẳng định nào đúng?

A. $f(3) < f(-2)$
B. $f(-3) < f(-2)$
C. $f(2) < f(0)$
D. $f(2) > f(3)$

Câu 3:

Cho hàm số $y = f(x)$ có đạo hàm liên tục trên $\mathbb{R}$. Hàm số $y = f'(x)$ có đồ thị như hình sau:

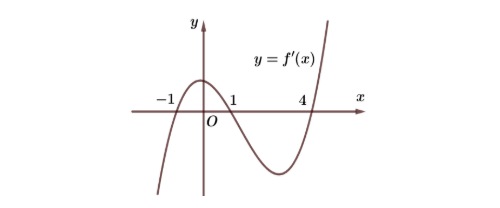
Trên đoạn $[-1; 4]$, giá trị lớn nhất của hàm số $y = f(x)$ là

A. $f(0)$
B. $f(-4)$
C. $f(-1)$
D. $f(1)$

Câu 4:

Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ:

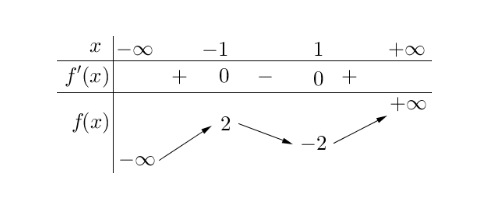
Giá trị nhỏ nhất của hàm số $y = f(x)$ trên khoảng $(-2; +\infty)$ là

A. $\min_{(-2;+\infty)} f(x) = -2$
B. $\min_{(-2;+\infty)} f(x) = 2$
C. $\min_{(-2;+\infty)} f(x) = -1$
D. $\min_{(-2;+\infty)} f(x) = 1$

Câu 5:

Gọi $M, m$ lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y = x + \frac{4}{x^2}$ trên đoạn $[1; 4]$. Khi đó biểu thức $\log_m(9^M)$ có giá trị bằng

A. 18
B. 27
C. 10
D. 15

Câu 6:

Đường tiệm cận xiên của đồ thị hàm số $y = f(x) = \frac{x^2 + x + 1}{x + 1}$ có phương trình là

A. $y = x + 1$
B. $y = x$
C. $y = x – 1$
D. $y = 1$

Câu 7:

Tiệm cận ngang của đồ thị hàm số $y = \frac{2x + 1}{x – 1}$ là

A. $y = \frac{1}{2}$
B. $y = -1$
C. $y = 1$
D. $y = 2$

Câu 8:

Đồ thị của hàm số $y = -2x^3 + 3x^2 – 5$ cắt trục tung tại điểm có tung độ bằng

A. $-5$
B. $0$
C. $-1$
D. $2$

Câu 9:

Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án $A, B, C, D$ dưới đây. Hỏi hàm số đó là hàm số nào?

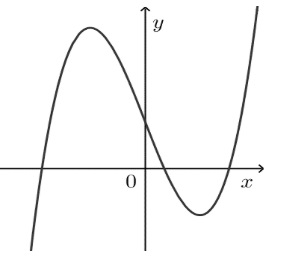
A. $y = x^3 – 3x + 1$
B. $y = -x^3 + 3x + 1$
C. $y = x^2 – x^2 + 1$
D. $y = -x^3 + x – 1$

Câu 10:

Hình vẽ sau đây là đồ thị của hàm số nào?

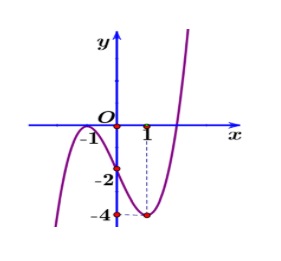
A. $y = x^3 – 3x + 2$
B. $y = -x^3 + 3x – 2$
C. $y = x^3 – 3x – 2$
D. $y = \frac{1}{3}x^3 – \frac{7}{3}x + 2$

Câu 11:

Bảng biến thiên trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án $A, B, C, D$ dưới đây. Hỏi hàm số đó là hàm số nào?

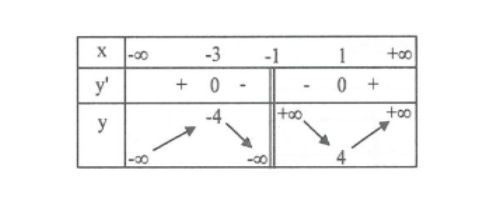
A. $y = \frac{x^2 – 2x}{x + 1}$
B. $y = \frac{x^2 + 3x}{x + 1}$
C. $y = \frac{1 – x^2}{x}$
D. $y = \frac{x^2 + 2x + 5}{x + 1}$

Câu 12:

Cho hình lăng phương $ABCD.A_1B_1C_1D_1$. Gọi $O$ là tâm của hình lăng phương. Chọn đẳng thức đúng?

A. $\overrightarrow{AO} = \frac{1}{3}(\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA_1})$
B. $\overrightarrow{AO} = \frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA_1})$
C. $\overrightarrow{AO} = \frac{1}{4}(\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA_1})$
D. $\overrightarrow{AO} = \frac{2}{3}(\overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA_1})$

Phần 2. Trắc nghiệm lựa chọn đúng sai

Thí sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 13:

Cho hàm số $f(x) = \frac{2x-1}{x+3}$.

a) Hàm số $f(x)$ có tiệm cận đứng $x = -3$.

b) Hàm số $f(x)$ đồng biến trên khoảng $(-\infty; +\infty)$.

c) $f(x) < f(x+1) \forall x \geq 0$.

d) Hàm số đạt cực tiểu tại $x = -3$.

Câu 14:

Cho hàm số $f(x) = \frac{x^2 – 2x + 5}{x – 1}$

Xét tính Đúng – Sai trong các khẳng định sau:

a) Hàm số có đạo hàm là $f'(x) = \frac{x^2 + 2x – 3}{(x-1)^2}$.

b) Hàm số đồng biến trên các khoảng $(-\infty; -1)$ và $(4; +\infty)$.

c) Hàm số có giá trị cực tiểu bằng $3$.

d) Hàm số $y = f(x^2 – 1)$ có $3$ cực tiểu.

Câu 15:

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật. Biết rằng: cạnh $AB = a$, $AD = 2a$, cạnh bên $SA = 2a$ và vuông góc với mặt đáy. Gọi $M$, $N$ lần lượt là trung điểm của các cạnh $SB$, $SD$. Xét tính đúng sai của các khẳng định sau

a) Hai vector $\overrightarrow{AB}$, $\overrightarrow{CD}$ là hai vector cùng hướng.

b) Góc giữa hai vector $\overrightarrow{SC}$ và $\overrightarrow{AC}$ bằng $60°$.

c) Tích vô hướng $\overrightarrow{AM} \cdot \overrightarrow{AB} = \frac{a^2}{2}$.

d) Độ dài của vector $\overrightarrow{AM} – \overrightarrow{AN}$ là $\frac{a\sqrt{3}}{2}$.

Câu 16:

Trong mặt phẳng tọa độ $Oxyz$, cho các điểm $A(1; -1; 2)$, $B(-1; 3; -4)$, $C(2; -3; 5)$

a) Điểm $A$ không nằm trong mặt phẳng $(Oyz)$.

b) Trọng tâm tam giác $OAB$ là $G(0; 1; -1)$.

c) Vector $\overrightarrow{AB}$ cùng phương vector $\overrightarrow{AC}$.

d) Điểm $M$ thuộc đoạn thẳng $AB$ sao cho $MA = 2MB$ có tọa độ $M\left(\frac{1}{2}; 1; 1\right)$

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn

Thí sinh trả lời từ câu 17 đến câu 22

Câu 17:

Hàm số $y = \frac{mx + 2}{x – 2}$ nghịch biến trên từng khoảng xác định khi $m \in (a; +\infty)$. Giá trị của $a$ bằng?

Câu 18:

Cho hàm số $y = f(x) = ax^3 + bx^2 + cx + d$ có đồ thị $(C)$. Biết $y = f'(x)$ có đồ thị như hình vẽ và tâm đối xứng của đồ thị $(C)$ thuộc trục hoành. Tính khoảng cách giữa hai điểm cực trị của đồ thị $(C)$. (Quy tròn kết quả đến hàng phần trăm)

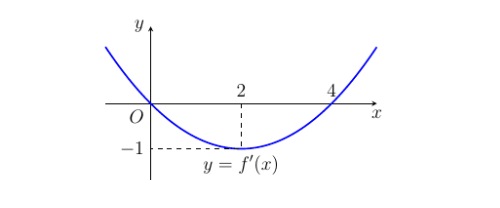
Câu 19:

Công ti truyền hình cáp Vista hiện có 100000 thuê bao. Mỗi thuê bao đang trả các khoản thuê bao 40$ tháng. Một cuộc khảo sát cho thấy cứ mỗi lần giảm $0.25$ cuộc thuê bao, công ti có thể có thêm 1000 thuê bao. Để doanh thu thu được là tối đa, công ti cần xác định mức cuộc thuê bao mỗi tháng là bao nhiêu?

Câu 20:

Có bao nhiêu giá trị nguyên $m \in [-10; 10]$ sao cho đồ thị hàm số $y = \frac{x – 1}{3x^2 + 6x + m – 2}$ có hai đường tiệm cận đứng?

Câu 21:

Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật $ABCD$, mặt phẳng $(ABCD)$ song song với mặt phẳng nằm ngang. Khung sắt độ được bước vào móc $E$ của chiếc xe cần cẩu sao cho tâm của đáy cáp $EA, EB, EC, ED$ có độ dài bằng nhau và cùng tạo với mặt phẳng $(ABCD)$ một góc bằng $60°$. Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng.

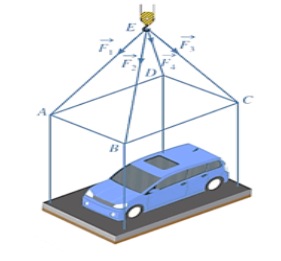
Tính trọng lượng của chiếc xe ô tô, biết rằng các lực căng $F_i$ đều có cường độ là $4700N$ và trọng lượng của khung sắt là $3000N$. (Kết quả làm tròn đến hàng đơn vị)

Câu 22:

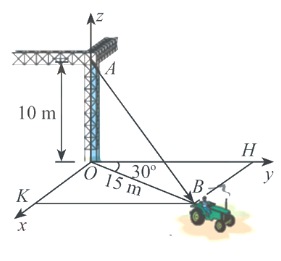
Một chiếc xe đang kéo căng sợi dây cáp $AB$ trong công trường xây dựng, trên độ dã thiết lập hệ tọa độ $Oxyz$ như hình vẽ dưới với độ dài đơn vị trên các trục tọa độ bằng $1m$. Biết $\overrightarrow{AB} = (x; y; z)$. Tính $x + y + z$ (làm tròn đến hàng phần chục).

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh