Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Câu 1:
Cho hàm số $f(x)$ có bảng biến thiên như sau:
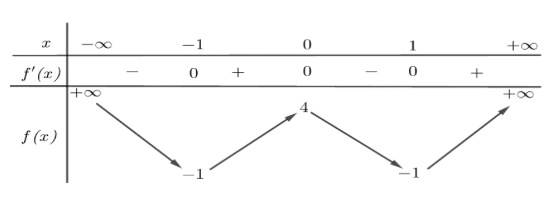
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. $(-\infty; -1)$
B. $(0; 1)$
C. $(-1; 1)$
D. $(-1; 0)$
Câu 2:
Cho hàm số $f(x)$ có bảng biến thiên như sau:
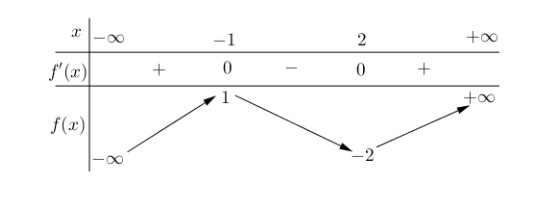
Hàm số đã cho đạt cực đại tại
A. $x = -2$
B. $x = 2$
C. $x = 1$
D. $x = -1$
Câu 3:
Cho hàm số $y = f(x)$ xác định và có đạo hàm trên $[0; +\infty)$. Đồ thị của đạo hàm bậc nhất $y = f'(x)$ được cho trong hình vẽ sau:
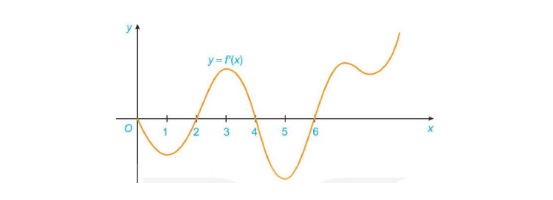
Khẳng định nào sau đây là đúng?
A. Hàm số $y = f(x)$ đồng biến trên khoảng $(1; 3)$
B. Hàm số $y = f(x)$ nghịch biến trên khoảng $(3; 5)$
C. Hàm số $y = f(x)$ đạt cực đại tại $x = 2$
D. Hàm số $y = f(x)$ có 2 cực tiểu, 1 cực đại
Câu 4:
Giá trị nhỏ nhất của hàm số $f(x) = \frac{x^2 – 2}{x – 1}$ trên đoạn $[2; 3]$ bằng
A. $\frac{7}{2}$
B. $\frac{5}{2}$
C. $2$
D. $1$
Câu 5:
Hàm số $y = f(x)$ liên tục trên đoạn $\left[-{1}; \frac{5}{2}\right]$ và có đồ thị như hình vẽ bên.
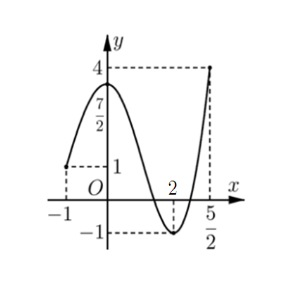
Gọi $M, m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn $\left[-{1}; \frac{5}{2}\right]$. Tính $M – 2m$.
A. $6$
B. $5$
C. $4$
D. $7$
Câu 6:
Tìm tiệm cận đứng của đồ thị hàm số $y = \frac{x + 1}{x – 2}$.
A. $x = 1$
B. $y = 1$
C. $x = 2$
D. $y = 2$
Câu 7:
Tiệm cận ngang của đồ thị hàm số $y = \frac{x – 2}{x + 1}$ là
A. $y = -2$
B. $y = 1$
C. $x = -1$
D. $x = 2$
Câu 8:
Cho hàm số $y = 2x – 1 + \frac{2025}{x + 3}$ $(C)$. Khoảng cách từ $M(2; -1)$ đến tiệm cận xiên của đồ thị $(C)$ là
A. $\frac{2}{\sqrt{5}}$
B. $\frac{4}{\sqrt{5}}$
C. $2$
D. $4$
Câu 9:
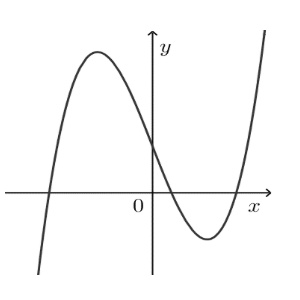
Đồ thị hàm số nào dưới đây có dạng như đường cong dưới đây?
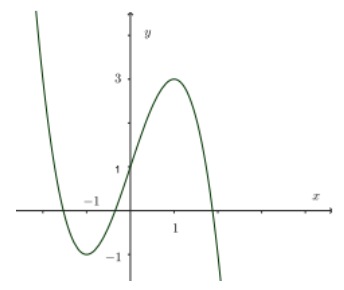
A. $y = \frac{2x – 1}{x + 1}$
B. $y = \frac{x^2 + 2x – 2}{x – 1}$
C. $y = -x^3 + 3x + 1$
D. $y = x^3 – 3x + 1$
Câu 10:
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
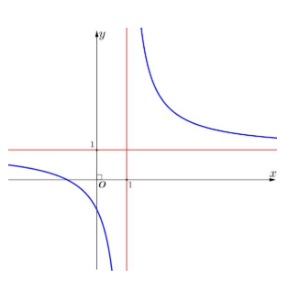
A. $y = \frac{x + 2}{x + 1}$
B. $y = x^2 – 2x – 1$
C. $y = \frac{x^2 – x + 1}{x – 1}$
D. $y = \frac{x + 1}{x – 1}$
Câu 11:
Cho hàm số $y = \frac{ax^2 + bx + c}{x}$ $(ac \neq 0)$ có đồ thị như Hình7. Đường tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng:
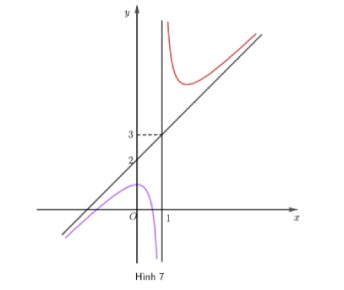
A. $y = x$
B. $y = 2x$
C. $x = 1$
D. $y = x + 2$
Câu 12:
Khi máu đi chuyển từ tim qua các động mạch chính rồi đến các mao mạch và quay trở lại tim qua các tĩnh mạch, huyết áp tâm thu (tức là áp lực của máu lên động mạch khi tim co bóp) liên tục giảm xuống. Giả sử một người có huyết áp tâm thu P (tính bằng mmHg) được cho bởi hàm số $P(t) = \frac{2t^2 – 90}{t^2 + 1}$ $(0 \leq t \leq 10)$, trong đó thời gian $t$ được tính bằng giây. Tốc độ thay đổi của huyết áp sau 5 giây kể từ khi máu rời tim là:
A. $\frac{375}{13}$
B. $\frac{125}{13}$
C. $\frac{250}{169}$
D. $\frac{375}{169}$
Phần 2. Trắc nghiệm lựa chọn đúng sai
Thí sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13:
Cho hàm số $y = f(x) = \frac{x^2 – 5x + 7}{x – 3}$. Các mệnh đề sau đúng hay sai?
a) Hàm số đồng biến trên khoảng $(-\infty; 2)$ và $(4; +\infty)$.
b) Hàm số nghịch biến trên khoảng $(2; 4)$.
c) Giá trị cực tiểu của hàm số là $y = 3$.
d) Các điểm cực trị của đồ thị hàm số là $(2; -1), (4; 3)$.
Câu 14:
Cho hàm số $y = f(x) = \frac{(x – m)(2 – x)}{x^2 – 4x + 4}$ với $m$ là tham số. Các mệnh đề sau đúng hay sai?
a) Đồ thị hàm số có đúng một đường đường tiệm cận ngang là đường thẳng $y = 1$.
b) Đồ thị hàm số không có đường tiệm cận xiên.
c) Với $m = 3$, đồ thị hàm số có đúng hai đường tiệm cận.
d) Với mọi giá trị của tham số $m$, đồ thị hàm số luôn nhận đường thẳng $x = 2$ làm đường tiệm cận đứng.
Câu 15:
Cho hàm số $y = \frac{ax^2 + bx + c}{dx + e}$ có đồ thị là đường cong trong hình vẽ.
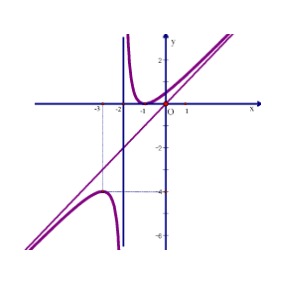
a) $\min_{(-2; +\infty)} y = -4$.
b) Khoảng cách giữa hai điểm cực trị của đồ thị bằng $2\sqrt{5}$.
c) Hàm số nghịch biến trên $(-2; -1)$.
d) Đồ thị hàm số có điểm cực đại $x = -3$.
Câu 16:
Một công ty sản xuất và bán sản phẩm với chi phí sản xuất được cho bởi hàm: $C(x) = 500 + 40x$ và doanh thu được cho bởi hàm: $R(x) = 100x – 0.5x^2$ trong đó $x$ là số lượng sản phẩm. Hỏi các khẳng định sau đúng hay sai?
a) Lợi nhuận $P(x)$ khi sản xuất và bán $x$ sản phẩm được tính bởi công thức $P(x) = R(x) – C(x)$
b) Đạo hàm của hàm lợi nhuận $P'(x)$ cho biết tốc độ thay đổi lợi nhuận theo số lượng sản phẩm.
c) Điểm tối ưu, tức là điểm mà lợi nhuận đạt cực đại, xảy ra khi $P'(x) = 0$.
d) Số lượng sản phẩm tối ưu mà công ty nên sản xuất và bán là 80 đơn vị.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn
Thí sinh trả lời từ câu 17 đến câu 22
Câu 17:
Có tất cả bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $y = \frac{x + m}{x + 2023}$ đồng biến trên từng khoảng xác định của nó.
Câu 18:
Có tất cả bao nhiêu giá trị thực của tham số $m$ để hàm số $y = \frac{2}{3}x^3 – mx^2 – 2(3m^2 – 1)x + \frac{2}{3}$ có hai điểm cực trị $x_1, x_2$ sao cho $x_1x_2 + 2(x_1 + x_2) = 1$
Câu 19:
Một nhà máy làm bao bì muốn sản xuất các vỏ hộp dạng hình hộp chữ nhật có thể tích $216cm^3$ và đáy hộp là hình vuông. Tìm chiều cao (cm) của hộp sao cho chi phí làm vỏ hộp là nhỏ nhất.
Câu 20:
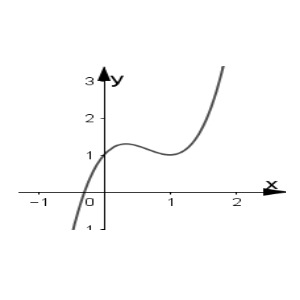
Hàm số $y = ax^3 + bx^2 + cx + d$ có đồ thị như hình vẽ bên dưới. Hỏi có tất cả bao nhiêu số dương trong các số $a, b, c, d$?
Câu 21:
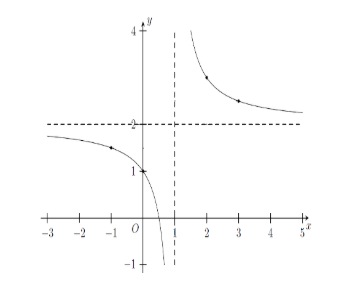
Cho hàm số $y = \frac{ax – 1}{bx + c}$ có đồ thị như dưới đây. Giá trị biểu thức $T = a + 2b + 3c$ bằng
Câu 22:
Một công ty sản xuất sản phẩm B. Lợi nhuận thu được khi sản xuất và bán $x$ sản phẩm là $P(x) = -x^3 + 6x^2 + 15x – 20$ (đơn vị: triệu đồng). Hỏi khi sản xuất bao nhiêu sản phẩm thì công ty đạt lợi nhuận lớn nhất?

ThS. Lê Thị Thuý Nga
(Người kiểm duyệt, ra đề)
Chức vụ: Trưởng ban biên soạn môn Toán THPT
Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1
Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh