PHẦN I. Câu trắc nghiệm nhiều phương án lực chọn

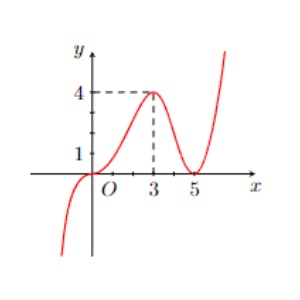
Câu 1. Cho hàm số $y = f(x)$ có đồ thị như hình vẽ. Hàm số $y = f(x)$ đồng biến trên khoảng nào?

A. $(5; +\infty)$.

B. $(3; 5)$.

C. $(0; 5)$.

D. $(3; +\infty)$.

Câu 2. Cho hàm số $y = f(x)$ xác định trên $\mathbb{R}$ và có bảng biến thiên như hình vẽ sau:

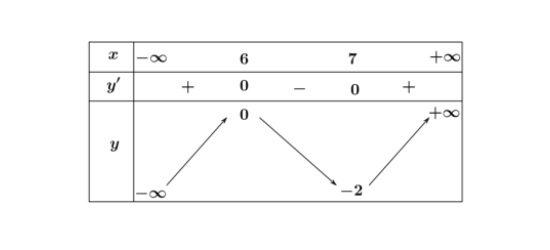
Tìm điểm cực đại của hàm số $y = f(x)$.

A. $x = 7$.

B. $x = -2$.

C. $x = 0$.

D. $x = 6$.

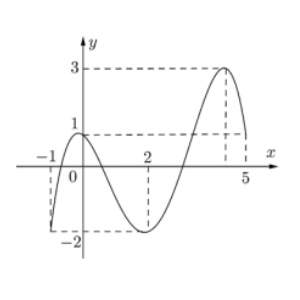
Câu 3. Cho hàm số $f(x)$ liên tục trên $[-1; 5]$ và có đồ thị trên đoạn $[-1; 5]$ như hình vẽ. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x)$ trên đoạn $[-1; 5]$ bằng:

A. $-1$.

B. $4$.

C. $1$.

D. $2$.

Câu 4. Một chất điểm chuyển động với vận tốc được cho bởi công thức $v(t) = -3t^2 + 12t + 1$ với $t$ (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động. Hỏi sau bao lâu khi chất điểm chuyển động thì đạt được vận tốc lớn nhất?

A. 2s

B. 1s.

C. 13s

D. 4s.

Câu 5. Cho hàm số $y = f(x)$ có $f(x) – 1$ và $f(x) = -1$. Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng $x = 1$ và $x = -1$.

B. Đồ thị hàm số đã cho không có tiệm cận ngang.

C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.

D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng $y = 1$ và $y = -1$.

Câu 6. Hàm số nào sau đây có một tiệm cận:

A. $y = \frac{x+3}{2x-1}$.

B. $y = \frac{2x}{x^2+1}$.

C. $y = \frac{4}{x-1}$.

D. $y = \frac{x^2+3x-2}{x+3}$.

Câu 7. Cho hàm số $f(x) = \frac{ax-6}{bx-c}$ ($a, b, c \in \mathbb{R}$) có bảng biến thiên như sau:

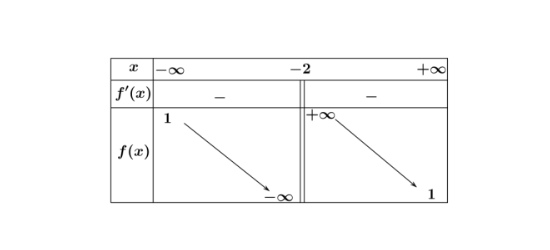
Trong các số $a, b, c$ có bao nhiều số âm?

A. 3.

B. 2.

C. 1.

D. 0.

Câu 8. Một bể chứa ban đầu có 100 lít nước. Sau đó, cứ mỗi phút người ta bơm thêm 20 lít nước, đồng thời cho vào bể 10 gam chất khử trùng (hòa tan). Hàm số $f(t)$ thể hiện nồng độ chất khử trùng (gam/lít) trong bể sau $t$ phút là:

A. $f(t) = \frac{20t+100}{10t}$.

B. $f(t) = 20t + 100$.

C. $f(t) = \frac{10t}{20t+100}$.

D. $f(t) = 20, 02t + 100$.

Câu 9. Đồ thị bên dưới là tốc độ của một chiếc xe đua trên đoạn đường dài 3km.

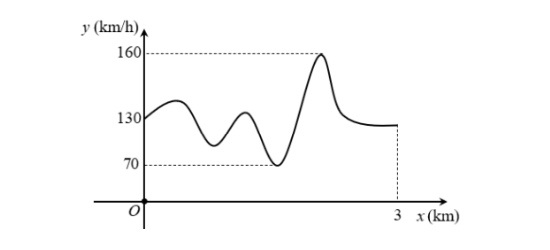
Tốc độ nhỏ nhất của xe đua trên đoạn đường này bằng:

A. 3 (km/h).

B. 160 (km/h).

C. 130 (km/h).

D. 70 (km/h).

Câu 10. Trong không gian cho tam giác $ABC$ có $G$ là trọng tâm và điểm $M$ nằm ngoài mặt phẳng $(ABC)$. Khẳng định nào sau đây là đúng?

A. $\overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} = \vec{0}$.

B. $\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \vec{0}$.

C. $\overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} = \overrightarrow{MG}$.

D. $\overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} = 3\overrightarrow{MG}$.

Câu 11. Cho hình chóp $S.ABC$ có $AB = 4$, $\widehat{BAC} = 60°$, $\overrightarrow{AB}.\overrightarrow{AC} = 6$. Khi đó độ dài $\overrightarrow{AC}$ là:

A. 3

B. 6

C. 4

D. 12.

Câu 12. Số các giá trị nguyên của tham số $m$ thuộc $[-2023; 2023]$ để đồ thị hàm số $y = \frac{2x+4}{x-m}$ có tiệm cận đứng nằm bên trái trực tung là:

A. 4044.

B. 2022.

C. 2023.

D. 4046.

PHẦN II. Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1. Cho hàm số $y = f(x)$ có đạo hàm liên tục trên $\mathbb{R}$. Hàm số $y = f'(x)$ có đồ thị như hình dưới đây.

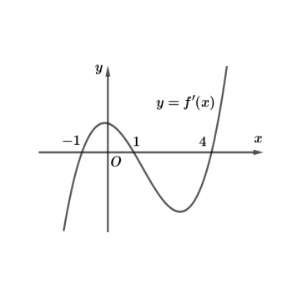
a) Hàm số $y = f(x)$ có hai cực trị.

b) Hàm số $y = f(x)$ đồng biến trên khoảng $(1; +\infty)$.

c) $f(1) > f(2) > f(4)$.

d) Trên đoạn $[-1; 4]$ thì giá trị lớn nhất của hàm số $y = f(x)$ là $f(1)$.

Câu 2. Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm. Khoảng cách từ tàu đổ bộ đến mặt đất Mặt Trăng được tính bằng hàm số đa thức bậc ba đầu tiên kể từ khi đốt cháy các tên lửa hãm, đó cao $h$ của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm $h(t) = -0, 01t^3 + 1, 1t^2 – 30t + 250$ trong đó $t$ là thời gian tính bằng giây và $h$ là độ cao tính bằng ki-lô-mét.

a) Trong 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao lớn nhất mà con tàu đạt được là 250 (km).

b) Trong khoảng 20 giây đầu kể từ khi đốt cháy các tên lửa hãm có độ cao luôn tăng.

c) Trong 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, vận tốc của con tàu lớn nhất đạt được là 10,33 (km/s)

d) Trong khoảng 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao thấp nhất mà con tàu đạt được tại thời điểm $t ≈ 25$ (s).

Câu 3. Cho tứ diện đều $ABCD$ cạnh $a$, $E$ là điểm trên đoạn $CD$ sao cho $ED = 2CE$.

a) Có 6 vectơ (khác vectơ $\vec{0}$) có điểm đầu và điểm cuối được tạo thành từ các đỉnh của tứ diện.

b) Góc giữa hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{BC}$ bằng $60°$.

c) Nếu $\overrightarrow{BE} = m\overrightarrow{BA} + n\overrightarrow{BC} + p\overrightarrow{BD}$ thì $m + n + p = \frac{2}{3}$.

d) Tích vô hướng $\overrightarrow{AD}.\overrightarrow{BE} = \frac{a^2}{6}$.

Câu 4. Cho hình lập phương $ABCD.EFGH$ có các cạnh bằng $a$. Khi đó:

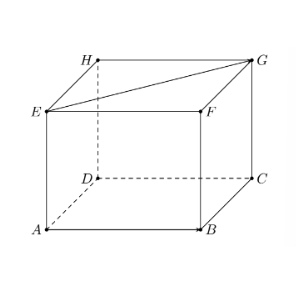
a) $\overrightarrow{DF} = \overrightarrow{DH} + \overrightarrow{DA} + \overrightarrow{DC}$.

b) Hai vectơ $\overrightarrow{DA}$ và $\overrightarrow{BC}$ bằng nhau.

c) Tích vô hướng của hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{EG}$ bằng $a^2$.

d) Góc giữa hai vectơ $\overrightarrow{EG}$ và $\overrightarrow{GB}$ bằng $90°$.

PHẦN III. Câu trắc nghiệm trả lời ngắn.

Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1. Cho hàm số $f(x) = x^3 + (1 + m^2)x + 1$. Gọi $S$ là tập hợp tất cả các giá trị nguyên của tham số $m$ để giá trị lớn nhất của hàm số trên đoạn $[0; 1]$ không vượt quá 7. Hỏi tập $S$ có bao nhiều phần tử là số nguyên?

Câu 2. Nồng độ thuốc trong máu của một bệnh nhân $t$ giờ sau khi tiêm là $C(t)$ $(mg/ml)$ với $C(t)$ được cho bởi công thức $C(t) = \frac{0,4}{t^2+1} + 0, 013$. Tìm nồng độ thuốc tồn dư, tức là nồng độ thuốc vẫn còn trong cơ thể nạn nhân trong dài hạn.

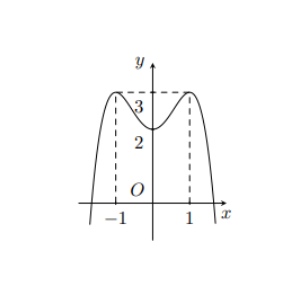
Câu 3. Cho hàm số $y = f(x)$ có đồ thị như hình vẽ. Số nghiệm của phương trình $f^2(x) – f(x) = 2$ là bao nhiều?

Câu 4. Cho tứ diện $ACBD$. Trên các cạnh $AD$ và $BC$ lần lượt lấy $M, N$ sao cho $AM = 3MD$, $BN = 3NC$. Gọi $P, Q$ lần lượt là trung điểm của $AD$ và $BC$. Ta có: $\overrightarrow{MN} = a\overrightarrow{PQ} + b\overrightarrow{DC}$. Tính $a + 2b$.

Câu 5. Cho biết công $A$ (đơn vị: J) sinh bởi lực $\vec{F}$ tác dụng lên một vật được tính bằng công thức $A = \vec{F}.\vec{d}$, trong đó $\vec{d}$ là vectơ biểu thị độ dịch chuyển của vật (đơn vị của $|\vec{d}|$ là m) khi chịu lực tác dụng của lực $\vec{F}$.

Một xe tải có khối lượng 1,5 tấn đang di xuống trên một đoạn đường dốc có góc nghiêng so với phương nằm ngang là $5°$. Tính công sinh bởi trọng lực $P$ khi xe xuống hết đoạn đường dốc dài 50m (làm tròn đến hàng đơn vị), biết rằng trọng lực $\vec{P}$ được xác định bởi công thức $\vec{P} = m.\vec{g}$, với $m$ (đơn vị: kg) là khối lượng của vật và $\vec{g}$ là gia tốc rơi tự do có độ lớn $g = 9, 8 m/s^2$.

Câu 6. Cho hàm số $f(x)$ có đạo hàm $f'(x) = (x + 1)(x – 1)(x – 4), \forall x \in \mathbb{R}$. Có bao nhiều số nguyên $m < 20$ để hàm số $g(x) = f\left(\frac{2-x}{1+x} – m\right)$ đồng biến trên $(2; +\infty)$.

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh