PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12.

Trong mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1. Khẳng định nào dưới đây đúng?

A. $\int (2x + 5)dx = \frac{1}{2}x^2 + 5x + C$

B. $\int (2x + 5)dx = x^2 + C$

C. $\int (2x + 5)dx = 2x^2 + 5x + C$

D. $\int (2x + 5)dx = x^2 + 5x + C$

Câu 2. Hàm số $F(x) = \ln x$ xác định trên khoảng $(0; +\infty)$ là một nguyên hàm của hàm số nào sau đây?

A. $f(x) = \frac{1}{x^2}$

B. $f(x) = \frac{1}{x}$

C. $f(x) = -\frac{1}{x^2}$

D. $f(x) = -\frac{1}{x}$

Câu 3. Tìm họ nguyên hàm của hàm số $f(x) = x^{2025}$.

A. $\int f(x)dx = \frac{1}{2024}x^{2024} + C$

B. $\int f(x)dx = 2025.x^{2024} + C$

C. $\int f(x)dx = \frac{1}{2026}x^{2026} + C$

D. $\int f(x)dx = x^{2026} + C$

Câu 4. Tích phân $\int_a^b \frac{1}{x}dx$ bằng

A. $\ln b – \ln a$

B. $|\ln b| – |\ln a|$

C. $|\ln a| – |\ln b|$

D. $|\ln b| – |\ln |a||$

Câu 5. Họ nguyên hàm của hàm số $f(x) = 4x + \sin x$ là

A. $2x^2 + \cos x + C$

B. $4 + \cos x + C$

C. $2x^2 – \cos x + C$

D. $\frac{x^2}{2} – \cos x + C$

Câu 6. Cho $\int_{-3}^1 f(x)dx = 2$, $\int_1^3 f(x)dx = -5$. Tính $I = \int_{-3}^3 f(x)dx$.

A. -3

B. 0

C. 7

D. 6

Câu 7. Diện tích $S$ của hình phẳng giới hạn bởi đồ thị hàm số $y = x^2$, trục hoành $Ox$, các đường thẳng $x = 1$, $x = 2$ là

A. $S = \frac{7}{3}$

B. $S = \frac{8}{3}$

C. $S = 7$

D. $S = 8$

Câu 8. Tính thể tích của phần vật thể tạo nên khi quay quanh trục $Ox$ hình phẳng $D$ giới hạn bởi đồ thị $(P): y = 2x – x^2$ và trục $Ox$ bằng

A. $V = \frac{19\pi}{15}$

B. $V = \frac{13\pi}{15}$

C. $V = \frac{17\pi}{15}$

D. $V = \frac{16\pi}{15}$

Câu 9. Cho hàm số $y = x^2 – mx$ $(0 < m < 4)$ có đồ thị $(C)$. Gọi $S_1 + S_2$ là diện tích của hình phẳng giới hạn bởi $(C)$, trục hoành, trục tung và đường thẳng $x = 4$ (phần tô đậm trong hình vẽ bên dưới). Giá trị của $m$ sao cho $S_1 = S_2$ là

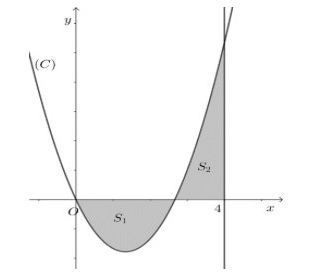
A. $m = 3$

B. $m = \frac{10}{3}$

C. $m = 2$

D. $m = \frac{8}{3}$

Câu 10. Trong không gian $Oxyz$ cho mặt phẳng $(P): 3x – y + z – 5 = 0$. $(P)$ có một véc-tơ pháp tuyến là:

A. $\overrightarrow{n} = (3; 1; 1)$

B. $\overrightarrow{n} = (6; -2; 2)$

C. $\overrightarrow{n} = (-3; 1; 1)$

D. $\overrightarrow{n} = (-1; 1; -5)$

Câu 11. Trong không gian với hệ tọa độ $Oxyz$, phương trình nào được cho dưới đây là phương trình mặt phẳng $(Oxz)$?

A. $x = y + z$

B. $y – z = 0$

C. $y + z = 0$

D. $x = 0$

Câu 12. Trong không gian hệ tọa độ $Oxyz$, cho ba điểm $A(1; -1; -1)$, $B(1; 0; 4)$, $C(0; -2; -1)$. Viết phương trình mặt phẳng $(\alpha)$ qua $A$ và vuông góc với đường thẳng $BC$.

A. $x + 2y + 5z + 6 = 0$

B. $x + 2y + 5z – 5 = 0$

C. $x – 2y – 5z – 6 = 0$

D. $x – 2y – 5z + 6 = 0$

PHẦN II. Thí sinh trả lời các câu 13, 14.

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 13. Hàm số $F(x)$ là một nguyên hàm của hàm số $f(x) = 3x^2 + 2$ trên $\mathbb{R}$.

a) $F'(1) = 6$.

b) Hàm số $F(x) + 2$ là một nguyên hàm của hàm số $f(x)$.

c) Mọi nguyên hàm của hàm số $f(x)$ có dạng $F(x) + C$ với $C$ là hằng số thực.

d) Nếu $F(\sqrt{2}) – F(1) = m\sqrt{2} + n$ ($m$ và $n$ là các số nguyên) thì $m + n = 1$.

Câu 14. Trong không gian với hệ trục tọa độ $Oxyz$, cho điểm $A(1; 3; 2)$ và mặt phẳng $(\alpha): 3x – y + z – 1 = 0$.

a) $\overrightarrow{n} = (3; 1; 1)$ là một vector pháp tuyến của $(\alpha)$.

b) $(\alpha)$ đi qua điểm $A$.

c) $d(A; \alpha) = \frac{\sqrt{11}}{11}$.

d) Mặt phẳng đi qua điểm $A$ và song song với $(\alpha)$ có phương trình $3x – y + z – 2 = 0$.

PHẦN III. Thí sinh trả lời từ câu 15 đến câu 19

Câu 15. Biết $I = \int_1^5 \frac{2|x – 2| + 1}{x}dx = 4 + a\ln 2 + b\ln 5$ với $a, b \in \mathbb{R}$. Tính $S = a + b$.

Câu 16. Một chất điểm $A$ xuất phát từ $O$, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật $v(t) = \frac{1}{180}t^2 + \frac{11}{18}t$ (m/s), trong đó $t$ là khoảng thời gian tính từ lúc $A$ bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm $B$ cũng xuất phát từ $O$, chuyển động thẳng cùng hướng với $A$ nhưng chậm hơn 5 giây so với $A$ và có gia tốc bằng $a$ (m/s²) ($a$ là hằng số). Sau khi $B$ xuất phát được 10 giây thì đuổi kịp $A$. Vận tốc của $B$ tại thời điểm đuổi kịp $A$ bằng

Câu 17. Trên thiết kế đồ họa 3D của một cánh đồng điện mặt trời trong không gian $Oxyz$, một tấm pin năm trên mặt phẳng $(P): x – 3y + 4z + 5 = 0$; một tấm pin khác năm trên mặt phẳng $(Q)$ đi qua điểm $M(1; 3; -1)$ và song song với mặt phẳng $(P)$. Biết rằng phương trình mặt phẳng $(Q)$ có dạng $ax + by + 4z + c = 0$. Khi đó giá trị $a + b + c$ bằng bao nhiêu?

Câu 18. Một công trình đang xây dựng được gắn hệ trục $Oxyz$ (đơn vị trên mỗi trục tọa độ là mét). Ba bức tường lần lượt thuộc các mặt phẳng $(P), (Q), (R)$ (như hình vẽ) của tòa nhà lần lượt có phương trình: $(P): x + y – 2z + 1 = 0$, $(Q): x + y + z – 5 = 0$, $(R): 2x + 2y – 4z + 21 = 0$.

Độ rộng của bức tường thuộc mặt phẳng $(Q)$ của tòa nhà bằng bao nhiêu mét? (kết quả làm tròn đến hàng phần chục)

Câu 19. Cho $\int_0^1 \frac{xdx}{(2x + 1)^2} = a + b\ln 3$ với $a, b$ là các số hữu tỉ. Giá trị của $a + b$ bằng bao nhiêu?

PHẦN IV. Câu hỏi tự luận

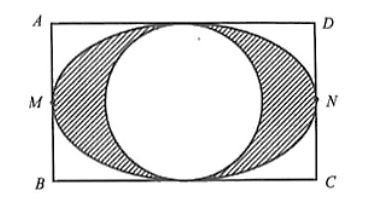
Câu 20. Một vật trang trí có dạng một khối tròn xoay được tạo thành khi quay miền $(R)$ (phần gạch chéo trong hình vẽ) quanh trục $MN$. Biết rằng $ABCD$ là hình chữ nhật với $AB = 6cm$, $AD = 10cm$, $M$, $N$ lần lượt là trung điểm của $AB$, $CD$, hai đường cong là đường elip có hình chữ nhật cơ sở là $ABCD$ và đường tròn tiếp xúc với hai cạnh $AD$ và $BC$ (tham khảo hình vẽ). Tính thể tích của vật trang trí đó (kết quả làm tròn đến hàng phần chục)

Câu 21. Trong không gian với hệ tọa độ $Oxyz$ cho mặt phẳng $(P)$ đi qua điểm $M(9;1;1)$ cắt các trục $Ox, Oy, Oz$ tại $A, B, C$ ($A, B, C$ không trùng với gốc tọa độ). Thể tích tứ diện $OABC$ đạt giá trị nhỏ nhất là bao nhiêu?

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh