PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1: [Mức độ 1] Cho hàm số $f(x)$ xác định trên khoảng $K$. Hàm số $F(x)$ là một nguyên hàm của hàm số $f(x)$ trên khoảng $K$. Mệnh đề nào dưới đây sai?

A. $F(x) = f'(x)$

B. $F'(x) = f(x)$

C. $\left(\int f(x)dx\right)’ = F'(x)$

D. $\int f(x)dx = F(x) + C$

Câu 2: [Mức độ 1] Tìm nguyên hàm của hàm số $f(x) = \cos 3x$.

A. $\int \cos 3x dx = 3\sin 3x + C$

B. $\int \cos 3x dx = \frac{\sin 3x}{3} + C$

C. $\int \cos 3x dx = \sin 3x + C$

D. $\int \cos 3x dx = -\frac{\sin 3x}{3} + C$

Câu 3: [Mức độ 1] Cho hai hàm số $f(x)$, $g(x)$ liên tục trên đoạn $[c; d]$ và số thực $k$. Trong các khẳng định sau, khẳng định nào sai?

A. $\int_c^d [f(x) + g(x)]dx = \int_c^d f(x)dx + \int_c^d g(x)dx$

B. $\int_c^d [f(x) – g(x)]dx = \int_c^d f(x)dx – \int_c^d g(x)dx$

C. $\int_c^d [f(x).g(x)]dx = \int_c^d f(x)dx.\int_c^d g(x)dx$

D. $\int_c^d kf(x)dx = k\int_c^d f(x)dx$

Câu 4: [Mức độ 2] Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$. Biết hàm số $F(x)$ là một nguyên hàm của $f(x)$ trên $\mathbb{R}$ và $F(2) = 6, F(4) = 12$. Tích phân $\int_2^4 f(x)dx$ bằng

A. 2

B. 18

C. -6

D. 6

Câu 5: [Mức độ 1] Nếu $\int_{-1}^2 f(x)dx = -3$ thì $\int_2^{-1} f(x)dx$ bằng

A. 5

B. 4

C. -1

D. 3

Câu 6: Gọi $S$ là diện tích hình phẳng được tô đậm trong hình vẽ bên.

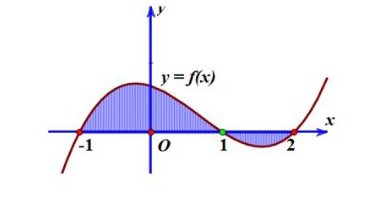
Công thức tính $S$ là

A. $\int_{-1}^1 f(x)dx + \int_1^2 f(x)dx$

B. $\int_{-1}^1 f(x)dx – \int_1^2 f(x)dx$

C. $\int_{-1}^2 f(x)dx$

D. $-\int_{-1}^2 f(x)dx$

Câu 7: Thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số $y = x^2$; trục $Ox$; $x = 1; x = 3$ quay quanh trục $Ox$ là:

A. $V = \frac{242}{5}$

B. $V = \frac{26}{3}$

C. $V = \frac{26\pi}{3}$

D. $V = \frac{242\pi}{5}$

Câu 8: Cho mặt phẳng $(P): 2x + 3y + 5z – 4 = 0$ và mặt phẳng $(Q) // (P)$. Vector nào sau đây là một vector pháp tuyến của mặt phẳng $(Q)$.

A. $(2; 3; -5)$

B. $(2; -3; -5)$

C. $(-4; -6; 10)$

D. $(4; 6; 10)$

Câu 9: Viết phương trình tổng quát của mặt phẳng $(P)$ biết $(P)$ chứa trục $Ox$ và $(P)$ đi qua điểm $M(1; 1; 2)$.

A. $x – y = 0$

B. $x + y – z = 0$

C. $2x – z = 0$

D. $2y – z = 0$

Câu 10: [Mức độ 2] Trong không gian cho điểm $M(1; 0; -1)$, mặt phẳng $(\alpha)$ qua M và chứa trục ox có phương trình là

A. $y = 0$

B. $x = 0$

C. $z = 0$

D. $x + z = 0$

Câu 11: [Mức độ 1] Trong không gian $Oxyz$, cho đường thẳng 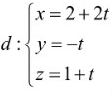. Một vector chỉ phương của đường thẳng $d$ là

A. $\overrightarrow{u} = (2; -1; 1)$

B. $\overrightarrow{v} = (2; 0; 1)$

C. $\overrightarrow{u} = (2; 1; -1)$

D. $\overrightarrow{u} = (2; 1; -1)$

Câu 12: [Mức độ 1] Trong không gian $Oxyz$, phương trình đường thẳng đi qua hai điểm $A(1; 2; 3), B(5; 4; -1)$ là

A. $\frac{x-1}{4} = \frac{y-2}{2} = \frac{z-3}{4}$

B. $\frac{x-5}{2} = \frac{y-4}{1} = \frac{z+1}{-2}$

C. $\frac{x+5}{-2} = \frac{y+4}{-1} = \frac{z-1}{2}$

D. $\frac{x+1}{4} = \frac{y+2}{2} = \frac{z+3}{-4}$

PHẦN II. Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Các mệnh đề sau đúng hay sai.

a) Nếu các hàm số $y = f(x), y = g(x)$ liên tục trên $K$ thì $\int [f(x) + g(x)]dx = \int f(x)dx + \int g(x)dx$.

b) $\int (2^x + e^x)dx = 2^x + e^x + C$.

c) Biết $F(x) = x^3$ là một nguyên hàm của hàm số $f(x)$ trên $\mathbb{R}$. Giá trị của $\int_1^3 (1 + f(x))dx$ bằng 28

d) Cho hàm số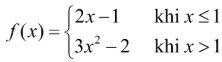. Khi đó $\int_{-1}^3 f(x)dx = 22$.

Câu 2: Cho đường tròn $(C)$ tâm $O$ bán kính bằng 2, cắt trục hoành tại hai điểm $A, B$. Parabol $(P)$ đi qua hai điểm $A, B$ và có tọa độ đỉnh $I(0; 1)$.

a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = f(x), y = g(x)$ và hai đường thẳng $x = a, x = b$ $(a < b)$ là $S = \int_a^b f(x) – g(x)dx$.

b) Diện tích hình phẳng giới hạn bởi đường tròn $(C)$, parabol $(P)$ bằng $\frac{a\pi – b}{c}$ với $a, b, c$ là các số tự nhiên, $c$ là phân số tối giản. Khi đó $a + b + c = 9$.

c) Thể tích vật thể khi xoay hình phẳng giới hạn bởi parabol $(P)$, trục hoành, hai đường thẳng $x = -2; x = 2$ bằng $\frac{m\pi}{n}$ với $m, n$ là số tự nhiên, $n$ là phân số tối giản. Khi đó $m – n = 7$.

d) Từ một quả cầu bằng đá trắng sứ bán kính bằng 2 dm, người ta khoét rút lõi ngay “chính giữa” quả cầu (trục đối xứng của lõi và quả cầu trùng nhau) như hình sau với đường kính mũi khoan là 2 dm được một vật thể có thể tích $V = \frac{32 – 12\sqrt{3}}{6}\pi$ (bỏ qua độ dày mũi khoan).

Câu 3: [Mức độ 2] Trong không gian với hệ tọa độ $Oxyz$, cho ba điểm $A(2; 1; 3)$, $B(3; 0; 2)$, $C(0; -2; 1)$.

a. [Mức độ 1] Tọa độ các vector $\overrightarrow{AB} = (1; -1; -1), \overrightarrow{AC} = (-2; -3; -2)$

b. [Mức độ 2] Phương trình mặt phẳng $(ABC)$ là: $x – 4y + 5z – 13 = 0$.

c. [Mức độ 2] Khoảng cách từ điểm $A$ đến mặt phẳng trung trực của đoạn thẳng $BC$ bằng $\frac{\sqrt{17}}{4}$.

d. [Mức độ 3] Mặt phẳng $(P)$ đi qua $A, B$ và cách $C$ một khoảng lớn nhất có phương trình $3x + 2y + z – 11 = 0$.

Câu 4: Trong không gian $Oxyz$, cho đường thẳng $d: \frac{x-2}{2} = \frac{y-2}{1} = \frac{z-3}{1}$ và mặt phẳng $(P): x + y + z – 3 = 0$.

a. [NB] Đường thẳng $d$ có một vector chỉ phương $\overrightarrow{u} = (2; 1; 1)$

b. [TH] Phương trình đường thẳng $\Delta$ đi qua $A(2; -1; 3))$ và song song với đường thẳng $d$ có phương trình tham số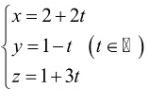

c. [TH] Gọi $M(x; y; z)$ là giao điểm giữa đường thẳng $d$ và mặt phẳng $(P)$, lúc đó $x + 2y – z = 2$

d. [VD] Phương trình đường thẳng $d”$ nằm trong mặt phẳng $(P)$ cắt và vuông góc với đường thẳng d là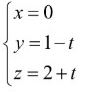

PHẦN III. Câu trắc nghiệm trả lời ngắn.

Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: [Mức độ 2] Cho $F(x)$ là một nguyên hàm của hàm số $f(x) = 3x^2 – e^x$ trên $\mathbb{R}$ thỏa mãn $F(0) = 3$. Giá trị của $F(1)$ bằng bao nhiêu? (làm tròn đến phần hàng trăm).

Câu 2: Trong không gian $Oxyz$, cho hai điểm $A(1; 2; -1), B(3; b; c)$, mặt phẳng $(\alpha): x + 3y – 2z – 7 = 0$ và đường thẳng 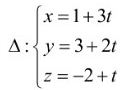. Khi đó, để đường thẳng $d$ đi qua hai điểm $A, B$ song song với mặt phẳng $(\alpha)$ và vuông góc với đường thẳng $\Delta$ thì $b + c$ bằng

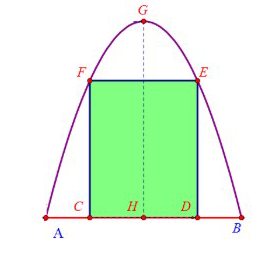
Câu 3: [Mức độ 3] Nhà bác An có một cái cổng hình Parabol như hình vẽ. Chiều cao $GH = 4m$, chiều rộng $AB = 4m$, $AC = BD = 0,9m$. Bác An làm hai cánh cửa khi đóng lại là hình chữ nhật $CDEF$ (phần tô đậm) có giá là $1,5$ triệu đồng/m², còn các phần để trang trí hoa có giá là $1,2$ triệu đồng/m². Hỏi tổng số tiền mà bác An phải trả để làm cửa và trang trí cho cổng là bao nhiêu (kết quả làm tròn đến hàng phần chục, đơn vị là triệu đồng)?

Câu 4: [Mức độ VD] Cho hình phẳng $H$ giới hạn bởi các đường $y = f(x) = x^2 – 8x + 12$ và $y = g(x) = -x + 6$. Khối tròn xoay tạo thành khi quay $H$ xung quanh trục hoành có thể tích bằng bao nhiêu? (Làm tròn đến hàng phần chục)

Câu 5: [Mức độ 3] Trong không gian $Oxyz$, cho điểm $A\left(-\frac{3}{2}, \frac{1}{2}, 0\right)$, mặt phẳng $(P): x – 2y + z + \frac{5}{2} = 0$ và mặt cầu $(S): x^2 + y^2 + z^2 – 2x – 6y – 15 = 0$. Gọi $\Delta$ là đường thẳng đi qua $A$ và $\Delta$ nằm trong mặt phẳng $(P)$ và cắt mặt cầu $(S)$ tại hai điểm $B, C$ sao cho tam giác $IBC$ có diện tích lớn nhất, với $I$ là tâm của mặt cầu $(S)$. Gọi $\overrightarrow{u_\Delta} = (-1; a; b)$ là vector chỉ phương của đường thẳng $\Delta$. Tính $a + b$.

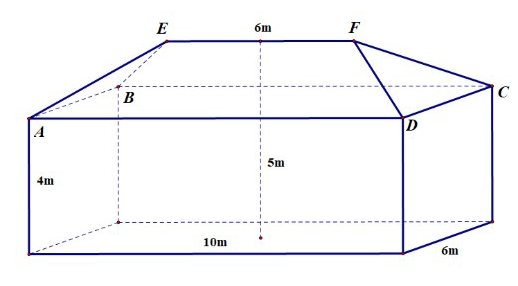
Câu 6. [Mức độ VD] Một ngôi nhà được mô tả bằng mô hình với tên của các đỉnh như hình vẽ. Bốn bức tường là các hình chữ nhật vuông góc với mặt sàn có chiều cao là $4m$. Mặt sàn là hình chữ nhật dài $10m$, rộng $6m$. Nhà có bốn mái với mái trước và mái sau là hai hình thang cân bằng nhau, hai mái bên là các hình tam giác cân bằng nhau. Đỉnh nóc là EF dài $6m$. Chiều cao của ngôi nhà là $5m$. Góc nhị diện tạo bởi mái trước và mái bên là bao nhiêu độ. (làm tròn đến hàng đơn vị)